空间到加权型空间的复合微分前置算子

余 建，伍鹏程

(贵州师范大学 数学科学学院，贵州 贵阳 550001)



空间到加权型空间的复合微分前置算子

余 建，伍鹏程*

(贵州师范大学 数学科学学院，贵州 贵阳 550001)

从算子的性质出发，研究Bloch空间到加权型空间的复合微分前置算子的有界性和紧性，得到了算子有界性和紧性的充分必要条件。

Bloch空间；加权型空间；复合微分前置算子；有界性；紧性

0 引言

记Δ为复平面上的单位开圆盘，H(Δ)为Δ上解析函数的全体，对u,φ∈H(Δ)) 且u(Δ)⊆Δ，文献[1]给出了u,φ为符号的复合微分前置算子: uDCφf=uφ′f′(φ)，其中f∈H(Δ)。

对f∈H(Δ)，文献[2]给出了Δ上Bloch空间和小Bloch空间的定义分别为:

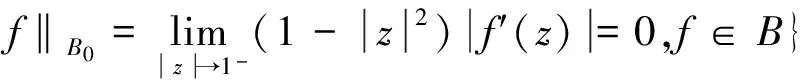
1 主要结果及证明

在这个部分，将给出主要结果和证明以及证明所要用到的引理(见文献[7])。

引理1的证明相仿文献[7]的定理3.11的证明，故省去。

定理1 设u,μ∈H(Δ)，u(Δ)⊆Δ，φ是Δ上的解析自映射。则以下结论等价：

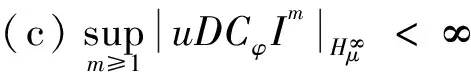
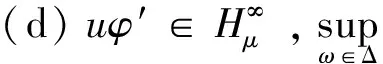
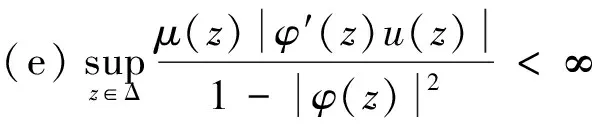
证明 (a)⟹(b)，显然。

(d)⟹(e) 对于λ∈Δ，作如下限制:

(1)

对任意固定的r∈(0,1)，由(1)有：

(2)

(3)

(e)⟹(a)对∀f∈B,z∈Δ，有：

定理2 设u,μ∈H(Δ)，u(Δ)⊆Δ，φ是Δ上的解析自映射。则以下结论等价：

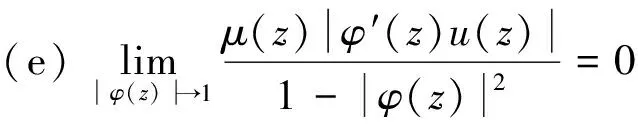
证明 (a)⟹(b)，显然。

(4)

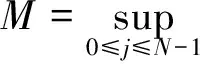
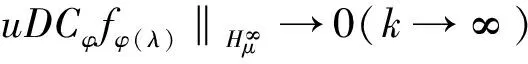
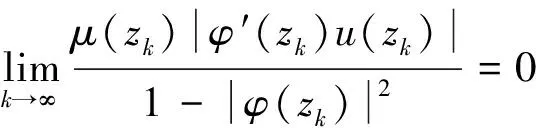
(5)

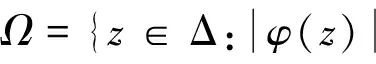
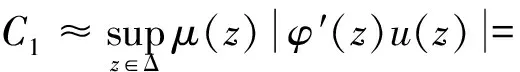
(6)

由(5)(6)两式得：

(7)

[1] 龙见仁.Q_k(p,q)空间到加权α-Bloch空间的复合微分后置和复合微分前置算子(英文)[J].贵州师范大学学报(自然科学版),2011，29(2):64-71.

[2] ZHU K.Bloch Type Spaces of Analytic-functions[J].Rocky Mountain Journal of Mathematics,1993,23(3):1143-1177.

[3] BIERSTEDT K D,SUMMERS W H.Biduals of weighted banach spaces of analytic functions[J].Journal of the Australian Mathematical Society,1993,54(1):70-79.

[4] LI S,STEVIC S.Composition followed by differentiation between H∞and α-Bloch spaces[J].Houston Journal of Mathematics,2009,35(1):327-340.

[5] ZHU X.Generalized weighted composition operators from Bloch spaces into Bers-type spaces[J].Filomat,2012,26(6):1163-1169.

[7] COWEN C C,MACCLUER B D.Composition Operators on Spaces of Analytic Functions, Studies in Advanced Mathematics[M].Boca Raton：CRC Press,1995.

Composition proceeded by differential operator from Bloch space to weighted-type space

YU Jian,WU Pengcheng*

(School of Mathematical Sciences, Guizhou Normal University, Guiyang, Guizhou 550001,China)

In this paper, the boundedness and compactness of the composite differential prior operator were studied, which was used to support the mapping, from Bloch space to the weighted space. And we obtained the necessary and sufficient conditions for the boundedness and compactness of this operator.

Bloch space; weighted space; composite differential prior operator; boundedness; compactness

1004—5570(2016)06-0056-03

2016-09-10

余 建(1990-),贵州师范大学硕士研究生，研究方向：函数论，E-mail：13765793029@139.com.

O175.2

A

*通讯作者：伍鹏程(1955-),教授,博士生导师，研究方向：函数论。