分支问题的有限决定性
黄得建 李艳青
(海南热带海洋学院 数学系,海南 三亚 572022)
分支问题的有限决定性
黄得建 李艳青
(海南热带海洋学院 数学系,海南 三亚 572022)
利用奇点理论的思想和方法研究了具有平凡解的分支问题.在t-等价群作用下,得到了具有平凡解的分支问题的t-有限决定性的充分条件,并且得到了εx,λ·{x}的εx,λ-子模余维有限的充要条件.
奇点理论;分支问题;等价群;t-有限决定性
0 引言
光滑函数芽的有限决定性是奇点理论中的一个比较重要的课题.为了将函数芽的研究由无限维化简为有限维,其有限决定性的理论显得非常重要.J.N.Mather[1]研究了关于群R对光滑函数芽的有限决定性;P.F.S.Porto[2]提出了光滑函数芽的相对有限决定性,即光滑函数芽关于R的子群的有限决定性;何伟和李养成[3]研究了代数集上光滑函数芽的相对有限决定性, L.C.Wilson[4]研究了光滑函数芽无限决定的充分必要条件,石昌梅,裴东河[5]定义了弱有限决定性和弱无限决定性,给出了函数芽的弱决定的充要条件.
本文主要应用奇点理论的方法,研究了分支问题在t-等价群作用下的有限决定性,给出了具有平凡解的分支问题t-有限决定的充分条件,并给出了εx,λ·{x}的εx,λ-子模余维有限的充要条件. 文中假定映射芽及函数芽均为光滑的,其它未解释的概念和记号可参见文献[6-8].
1 准备知识
将函数芽f:(R×R,0)→R组成的集合记为εx,λ,其中x是状态变量,λ为分支参数,那么εx,λ自然地构成环(也自然地构成一个R-代数). 类似地,函数芽Λ:(R,0)→R的集合记为ελ.如果g∈εx,λ满足g(0,0)=gx(0,0)=0,则称g是一个分支问题.如果分支问题满足g(0,λ)≡0,∀λ∈(R,0),则g称为具有平凡解的分支问题.易见,所有这样的分支问题均属于集合:
εx,λ·{x}={h∈εx,λ|h(x,λ)=f(x,λ)·x,∀f∈εx,λ}.
容易证明,εx,λ·{x}是εx,λ的子环,也是εx,λ-模.
引理[7](Nakayama引理)设A是含幺交换环(记幺元为1),I是A中的理想并且对于∀α∈I,1+α是A中的可逆元,假定M,N是A-模P的子模,M是有限生成的.如果M⊂N+I·M,则有M⊂N.
2 主要结果
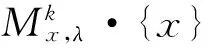
证明 由条件,g=fx,根据Taylor公式,g可以写作:
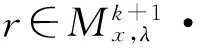
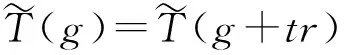
由轨道切空间的定义有
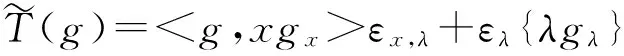
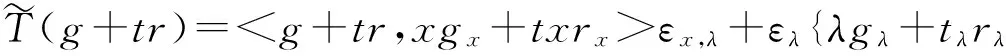
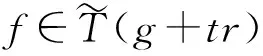
=ag+bxgx+cλgλ+tar+tbxrx+tcrλ,
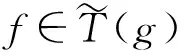
反过来,有
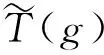
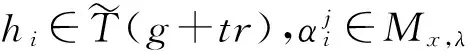
(1)
将(1)式用矩阵表示得
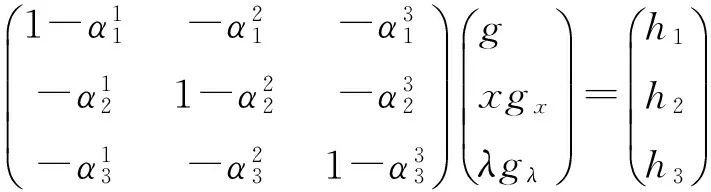
(2)
在(2)式中记
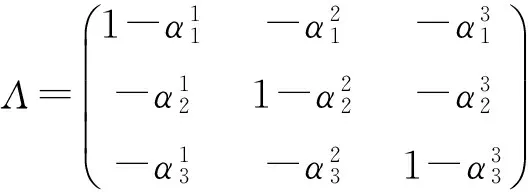
则Λ是εx,λ上的矩阵.因为detΛ=1+α,其中α∈Mx,λ,detΛ(0)=1故Λ是εx,λ上的可逆矩阵.从而,
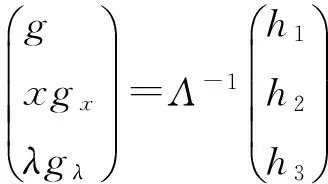
(3)
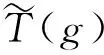
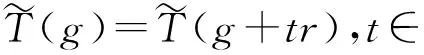
根据文献[8]中的定理1,有g~g+tr,t∈[0,1]从而有g~(jkf)·x.
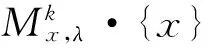
必要性 假定J余维有限,考虑:
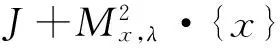
那么
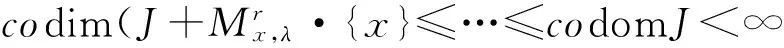
则存在k∈N,使得
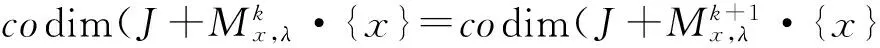
所以

因此有
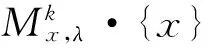
由Nakayama引理可得
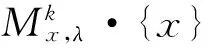
[1]Mather J. N. Stability of mappings Ⅲ:finitely determined map-germs [J]. Publ Math IHES,1968, 35:127-156.
[2]Porto P. F., S-Loibel G. F. Relative finite determinacy and relative stability of function-germs [J].Bol Soc Brasil Math, 1978,9(2):1-18.
[3]何伟,李养成.光滑函数芽的相对有限决定性[J].应用数学,2008,21(2):277-282.
[4]Wilson L. C. Infinitely determined map germs[J].Can J Math,1981,33(3):671-684.
[5]石昌梅,裴东河. 光滑函数芽的弱决定性[J].东北师大学报(自然科学版),2013,45(3):1-4.
[6]Golubitsky M., Schaeffer D. G. Singularities and Groups in Bifurcation Theory[M]. Vol.1 Applied Mathematical Sciences51.Springer-verlag,1985 .
[7]李养成.光滑映射的奇点理论[M].北京:科学出版社,2002.
[8]李艳青,李兵,黄得建.分支问题等价的一个充分条件[J].琼州学院学报,2009,12(2):4-6.
(编校:曾福庚)
The Finite Determinacy Of Bifurcation Probloms
HUANG De-jian, LI Yan-qing
(Department of Mathematics, Hainan Tropical Ocean University,Sanya Hainan 572022,China)
The bifurcation problems with trivial solution are discussed by using the methods in singularity theory. Under the action of thet- equivalent group, a sufficient condition for recognizing such bifurcation problems to bet- finite determinate is obtained. Besides, the necessary and sufficient conditions are proved aboutεx,λ-submodel inεx,λ·{x} with finite codimension.
singularity theory; bifurcation problem; equivalent group; finite determinacy
2015-10-22
琼州学院青年教师科研项目(QYQN201519);琼州学院青年教师科研项目(QYQN201520)
黄得建(1980-)男,河南太康人,海南热带海洋学院数学系讲师,硕士,研究方向为偏微分方程.
李艳青(1978-)女,河南武陟人,海南热带海洋学院数学系讲师,硕士,研究方向为奇点理论及应用和微分方程数值解.
0189.3
A
1008-6722(2016) 02-0010-03
10.1 3307/j.issn.1 008-6722.2 016.02.02

