在浪漫中精确，在精确中浪漫——以《最短路径》教学为例

●李玲

在浪漫中精确，在精确中浪漫
——以《最短路径》教学为例

●李玲

英国哲学家、数学家、教育家怀特海把人的认知过程分为三个阶段，即浪漫、精确、综合。浪漫阶段积累感官经验，精确阶段将感性认识上升到理性的概念层面，综合阶段就是运用知识。在灵活运用所学的过程中，人的视野不同了，就会产生新的好奇、新的浪漫，所以笔者认为，综合阶段是更“自由”的浪漫，它是新一轮“浪漫—精确—浪漫”的起点。

在教学时，笔者通过不断地制造“浪漫—精确—浪漫”的“认知漩涡”，将一个点的学习拉伸为一段旅程，让学生沉浸在知识发生、发现、发展的过程中。下面以《最短路径》的教学为例。

一、在浪漫中逐步精确

首先，将实际生活中的问题抽象成数学问题。

课前，笔者布置相关作业，给出了三个生活中的问题，要求学生理解并分析问题情境。

第一问为“将军饮马”，即将军凯旋而归，牵着他的战马去河边饮水，然后回营房休息，问马儿在何处饮水所走的路程之和最短？

第二问为“气泵选址”，即在天然气主管道的同侧有两个小区，要在主管道上安装一个气泵向两个小区输送天然气，气泵安装在何处能使铺设的管道用料最省？

第三问为“码头选址”，即湖中央有两个景点，游客要乘船游览两个景点，问码头修在何处，最能节省游船的燃料？

笔者要求学生将以上实际问题抽象成数学问题，并谈谈会有怎样的发现。去掉情境，学生们抽象出了同一个数学问题：在直线1上确定一点P，求到点A和点B的最小的距离之和。如图：

解决了这个数学问题就一并解决了这三个乃至生活中出现的这一类的问题。这里，观察关注生活，对生活中三个问题情境的理解与分析就是浪漫，抽象出其中的数学问题就是一次精确。

能够用数学的眼光观察生活，发现有价值的问题，这是解决问题的前提，更妙的是解决这一问题的意义感和挑战感又将激起学生进一步去探究，开启新一轮的浪漫。

其次，探究问题。

笔者请学生在直线上例举一些位置，经过测量和比较，得出结论：当P点选取的位置不同，PA+PB的值就不同。通过进一步举例、测量、比较后，学生就会发现，当P点在直线1上从左向右取时，PA+PB的值由大变小，然后又由小变大。此环节可以在学生动手的基础上用几何画板辅助，通过动态测量来演示。在演示过程中，学生断言，直线1上会有一点使PA+PB的值最小，并且探明了P点的大致位置。

“如果A、B分别在直线1的两侧就好了”，因为“两点之间线段最短”，部分学生产生这样的猜想，于是，他们就有了将其中一点“搬到”直线另一侧的想法。

而这只能是假想的“搬”，点B的位置是不会改变的，于是假想的那一点就不能在直线1的另一侧随意取，经过矫正与调控，便选定在点B关于直线1的对称的位置处。

解决问题的过程就是推理的过程，这个环节学生经历了推理和证明两个过程，得到并证明了如下结论：在直线上确定一点到同侧的两定点距离之和最短，即作其中任意一点的对称点，连接直线异侧的两点与直线的焦点即为所求。如图：

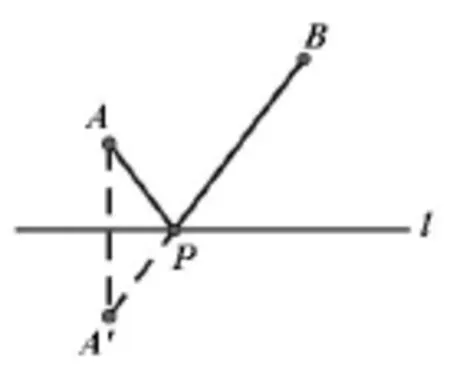
举例、测量、比较、猜想、联想、类比、矫正等一系列探究过程就是在充分的浪漫，最后得出的结论便是浪漫后的精确。

二、在精确中走向浪漫

首先，通过归纳相关类型题，建立模型。

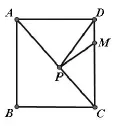
在得出结论后，笔者变换出题背景，给出例题1：正方形ABCD中，M是DC上一定点，P是对角线AC上一动点，P在何处时到点D和点M的距离之和最小。如图：

接着，笔者变换出题背景，给出例题2，等腰△ABC中（∠BAC为锐角），AH⊥BC于H，M是AC上一动点，AH上是否存在点P，使PC+PM最小。若存在找出P点的位置；若不存在，说明理由。如图：

学生在探究的过程中会发现，复杂几何背景下，例1进一步揭示了模型中的直线起对称轴的作用，因此这一类题通常以轴对称图形为出题背景。例2是动态问题中的最值，综合用到“两点之间线段最短”和“垂线段最短”，完整体现了“最短路径”问题的解题模型。通过变换不同的问题背景，引导学生用模型解释并解答问题，促使他们进一步认识到数学就是对生活的抽象，模型就是用数学的语言讲述现实世界的故事。

最后，请学生自主编题。这个环节便是到了入脑融合、明法慧生的“浪漫的自由”阶段，它能促使学生在不同情境中、不同的图形背景中牢牢抓住模型本质，从而实现知识的辨识和应用。模型沟通了数学与现实，于是这一环节又从抽象回归了现实，从精确走向了新的浪漫。可见，精确之后的应用会掀起新的浪漫。

其次，通过展开主题研讨，进一步拓展延伸。

在建立模型、学会运用后，笔者引导学生展开主题研讨：展示图片（公园里小道为什么修成弯道，上山的公路为什么不修成直的，高速公路为什么每隔一段会刻意修一个弯道或是起伏），请学生思考并举例，生活中有没有不走最短路径，刻意绕道走的情形？然后发起一个研讨：结合生活中这些现象谈谈你对捷径与弯路的理解。

如果前面抽象、建模环节都是体现知识的科学性的话，那么最后一个环节“主题研讨”则用来实现知识的人文性，达成情感、态度、价值观的三维目标。这个环节体现了对本节课的哲学思考，自然而又深刻地进行了价值观的引领。

精确之后的应用与思考掀起了新的浪漫，它让学生进入一个自由王国，这里可以有独立的思想、批判性的思维，不断迸发智慧的火花。学生们列举了盘山公路、河流遇阻时的绕道等等，说明弯曲才是人生的常态，面对挫折该有怎样的态度；有学生想到物理学中光的反射，找到知识间的联系……对这个话题学生很有话说，他们的认识角度很多，有的生动有创意，有的深刻有哲理。还有个学生说：“地球本是圆的，哪有直线给我们走？”学生的视角已经突破了平面的欧式几何范畴，进入到了宇宙空间。精确后的浪漫，力量是无穷的，它促使学生继续思考，研究感兴趣的方面，不停掀起“浪漫—精确—浪漫”的认知漩涡，生成新的智慧。

三、精确、浪漫之后的反思

在浪漫中精确，精确中浪漫是实现新课程标准的有效途径。修订后的《义务教育阶段数学课程标准》将过去的“双基”扩充为“四基”，“双基”指的是基本知识和基本技能，新增的“两基”即基本活动经验、基本数学思想，这个修订充分表达了专家组对知识获取过程和知识应用过程的重视。

本节课从浪漫到精确，从精确到浪漫，渗透了从特殊到一般再从一般到特殊的数学思想，经历了“问题情境——建立模型——解释与应用”和“实验——猜想——证明”的过程，学生积累下的是探索的活动性经验。

在浪漫中精确，精确中浪漫是对知识能动的掌握。本节课学习的知识在生活中固然重要，但对于学习者来说也可能终身都不会用到，然而在知识获取过程中，抽象能力、建模能力、推理能力却会相伴一生。知识是载体，获取的过程是重点，学生能动的参与建构是关键，获得的便是受益终身的智慧。

一切学问都是从生活中来的，是对自然和社会的观察中归纳出来的，书本大多呈现的是归纳的结果，而知识和原始观察有着什么联系，归纳证明的过程是怎样的，这才是学生最需要的东西。在“浪漫—精确—浪漫”的认知漩涡中，知识在增长，更重要的是认知的过程在被感知被认知，终将有一天，学生会走向自主发展的道路。

（作者单位：武汉经济技术开发区第一初级中学）

责任编辑 严芳