(强)余纯内射模和(强)余纯平坦模

张 珍(淄博师范高等专科学校 初教系 ，山东 淄博 255130)



(强)余纯内射模和(强)余纯平坦模

张 珍(淄博师范高等专科学校 初教系 ，山东 淄博 255130)

R是任意一个结合环，M既是左R-模又是右R-模。M称为强余纯内射的，如果对于任意的内射R-模E和任意的 i ≥ 1都有Exti(E, M ) = 0；如果 Ext1(E, M ) = 0，我们称M是余纯内射的。类似的，M称为余纯平坦的，如果对于任意的内射R-模E和任意的i ≥ 1都有Tori(E,M)=0；如果Tor1(E,M)=0 ，我们称M是余纯平坦的。我们找出并证明了(强)余纯内射模和(强)余纯平坦模之间的关系。更重要的是，我们给出了由Enochs and Jenda所列出的一些重要结论的证明。

余纯内射模；余纯平坦模，(预)盖类；(预)包类；余挠理论

2000 Mathematics Subject Classification: 13D02; 13D07; 13E15; 16D10

Introduction

Let R be an associative ring. R is called an Iwanaga-Gorenstein ring if R is both left and right noetherian and if the self-injective dimension on both the left and right is finite, [2]. In Homological algebra, injective precovers and flat preenvelopes caught many authors’ attention and the two classes of modules of copure injective and copure flat were discovered when studying the injective precovers and flat preenvelopes. Recently, the copure injective modules and copure flat modules have been studied by many authors, see [1], [3], [4], and [9].

In section 2 of this paper, we impose the definition of (strongly) copure injective modules, (strongly) copure flat modules and study the property of them. Furthermore, we investigate the equivalent condition of copure injective modules and strongly copure injective modules, copure flat modules and strongly copure flat modules. And we obtained a characterization for 1-Gorenstein ring. See the following Theorem

Theorem Let R be a left and right noetherian ring. The following are equivalent:

(1).R is 1-Gorenstein;

(2).An R-module (left and right) M is copure injective if and only if it is strongly copure injective;

(3).Every copure injective R-module (left and right) is h-divisible;

(4).Every homomorphic image of a copure injective R-module (left and right) is copure injective;

(5).Every h-divisible R-module (left and right) is copure injective;

(6).An R-module (left and right) M is copure flat if and only if it is strongly copure flat;

(7).Every submodule of a copure flat R-module (left and right) is copure flat;

(8).Every submodule of a flat R-module (left and right) is copure flat;

On the other hand, we imposed two new homological dimensions related to the class of copure injective modules and the class of copure flat modules, which we denote by cid and cfd respectively. And we proved the following two propositions, which were introduced by Enochs and Jenda [2]

Proposition Let R be a left and right noetherian ring and M a strongly copure flat R-module. The following are equivalent:

(1).R is n-Gorenstein;

(2).cidM≤ n for all left and right R-modules M ;

(3).If 0 → M → E0→ E1→…→ En-1→ C → 0 is an exact sequence of any left (right) R-module M with each Eiinjective, then C is strongly copure injective.

Proposition Let R be a left and right noetherian ring and M a strongly copure flat R-module. The following are equivalent:

(1).R is n-Gorenstein;

(2).cfdM ≤ n for all left and right R-modules M ;

(3).If 0 → K → Pn-1→ … → P1→ P0→ M → 0 is an exact sequence of any left (right) R-module M with each Piprojective, then K is strongly copure flat.

§1 Preliminaries

In this section, we introduce a number of notions and results which will be used throughout this work. Firstly, we employ some notions used by Holm in [6].

Definition 1.1. Let X be a class of R-modules and M be an R-module. An X-resolution of M is an exact sequence X=…→X1→X0→M→0with each Xi∈X. The X-coresolution of M is defined dually.

Let…→X1→X0→M→0 be an X-resolution of M . We set

K0= M , K1= ker(X0→ M ), Ki= ker(Xi-1→ Xi-2) for all i ≥ 2.

The nth kernel Kn(n ≥ 0) is called the nth X -syzygy of M.

Let 0→ M → X0→ X1→ … be an X -coresolution of M . We set

L0= M , L1= coker(M → X0), Li= ker(Xi-2→ Xi-1) for all i ≥ 2.

The nth cokernel Ln(n ≥ 0) is called the nth X -cosyzygy of M.

IfX is the class of projective (resp., injective) modules, then Kn(resp., Ln)is simply called the nth syzygy (resp.,cosyzygy).

We conclude this section by recalling the notion of cotorsion theory, which was first introduced by Salce in [11] for abelian groups, and which is a useful tool for showing the existence of (pre)covers and (pre)envelopes, see [2, Definitions 5.1.1 and 6.1.1].

Definition 1.3. [2, Definition 7.1.2] A pair of classes of modules (F , G ) is a cotorsion theory if F⊥= G and⊥G= F .

A set D is said to generate the cotorsion theory if⊥D = F and a set D′is said to cogenerate (F , G ) if D′⊥= G .

For a cotorsion theory (F , G ), we usually call F ∩ G the kernel of (F , G). A cotorsion theory (F, G) is called perfect if F is covering and G is enveloping, and (F, G ) is complete if F is special precovering, equivalently, G is special preenveloping [5, Lemma 2.2.6]. Note that a perfect cotorsion theory is always complete by [5, Corollary 2.2.5].A cotorsion theory(F,G)is hereditary if F is projectively resolving,equivalently,G is injectively resolving,or Ext 1 R(F.G)=0 for any F∈F and G∈G[5,Lemma 2.2.10].

In this section, we give the proof of the conclusion given by Enochs and Jenda.Moreover,we discussed the homological dimension related to the class of copure injective modules and copure flat modules.

Firstly,we give the definition of h-divisible modules.

Definition 2.1.Let R be any ring and M an R-module.M is called h-divisible if M is a homophic image of any injective R-module.

Now,we impose the definitions of(strongly)copure injective and (strongly)copure flat modules，which were defined by Enochs and Jenda in[2,Exercises 1,2]．

Definition 2.2. Let R be a ring. An Rmodule M is called strongly copure injective if Exti(E，M)=0for any injective R-module E andi 1, and M is called copure injective if Ext1(E,M)=0．

Definition 2.3.Let R be a ring. An Rmodule M is called strongly copure flat if Tory(E，M)=0 for any injective R-module E and i 1,and M is called copure flat if Tor1(E,M)=0．

The following Proposition indicates that the relation between (strongly)copure injective modules and(strongly)copure flat modules．

Proposition 2.4. Let R be a ring and E an injective R-modele(left and right)．Then an R-module M (left and right) is copure flat if and only if Hom(M，E)is copure injective.

Proof.By [2,Theotem 3.2.1]，we have the following is omorphism

Ext1(I，Hom(M，E)) Hom(Tor1(I,M),E)

wite I any injective R-modele (left and right)．Hence M is copure flat if and only if Hom(M，E)is copure injective．

The following Theorem was given by Enochs and Jenda，and we give the detailed proof．

Theorem 2.5.Let R be a left and right noetherian ring．The following are equivalent;

(1)．R is 1-Gorenstein;

(2)．An R-modele(left and right)M is copure injective if and only if it is strongly copure injective;

(3)．Every copure injective R-modele(left and right)is h-divisible；

(4)．Every homomorphic image of a copure injective R-modele(left and right)is copure injective；

(5)．Every h-divisible R-modele(left and right) is copure injective；

(6)．An R-modele(left and right) M is copure flat if and only if it is strongly copure flat；

(7)．Every submodule of a copure flat R-modele(left and right)is copure flat；

(8)．Every submodule of a flat R-modele (left and right)is copure flat；

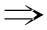
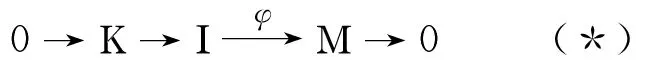
with I injective, and K the kernel of by Wakamatsu Lemma, Ext1(E, K) = 0 for any injective R-module (left and right) E. Therefore, K is copure injective. By (2), K is strongly copure injective. Applying Hom(E,-) to (*), we get a long exact sequence

… → Ext1(E, I ) → Ext1(E, M ) → Ext2(E, K) → …

Since Ext1(E, I ) = Ext2(E, K) = 0, we get that Ext1(E, M ) = 0. Hence M is copure injective.

0 → N → I → C → 0

with I injective and C the cokernel of(N → I) . So C is h-divisible module by Definition 2.1. For any R-module E (left and right), applyingHom(E,-), we get an isomorphism

Ext1(E,C)≅Ext2(E,N)

By (5), C is copure injective. So Ext1(E, C ) = 0, hence Ext2(E, N ) = 0. Therefore, pdE ≤ 1. By [2, Theorem 9.1.11], R is 1-Gorenstein.

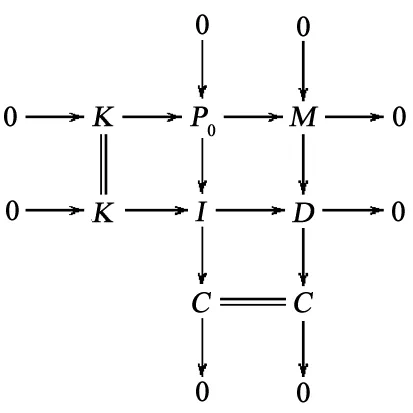
where the first row is the projective resolution of M and P0is projective. Consider the middle column, which is the injective resolution of P0with I injective. Since R is 1-Gorenstein, idP0≤ 1 by [2, Theorem 9.1.11(3)]. So C is injective. Hence the right most column in the pushout split and there is a morphism from D to M . So there is an epimorphism I → M and M is h-divisible.

→ Ext1(E, M ) → Ext1(E, N ) → Ext2(E, K) →

As Ext1(E, M ) = 0 = Ext2(E, K), we get that Ext1(E, N ) = 0. Hence N is copure injective and (4) follows.

0 → K → P0→ M → 0.

For any injective R-module E (left and right), applying E⊗ -, we get an isomorphism Tor1(E,K)≌ Tor1(E,M). Obviously, K is the submodule of P0, so K is copure flat by (8). Hence Tor1(E, K) = 0 and Tor2(E, M ) = 0 follows. Thus pdE ≤ 2. By [2, Theorem 9.1.11], R is 1-Gorenstein.

The copure injective dimension(cid) of an R-module M is the largest positive integer n such that Extn(E, M )≠0 for all injective E. For a strongly copure injective module M , we set cidM = 0. We have the following Proposition:

Proposition 2.6. Let R be a left and right noetherian ring and M a strongly copure injective R-module. The following are equivalent:

(1).R is n-Gorenstein;

(2).cidM ≤ n for all left and right R-modules M ;

(3).If 0 → M → E0→ E1→ … → En-1→ C → 0 is an exact sequence of any left (right) R-module M with each Eiinjective, then C is strongly copure injective.

0 → M → E0→ E1→ … → En-1→ C → 0,

applying Hom(E, -) with E an injective left (right) R-module, by dimension shifting, we get an isomorphism Exti(E,C)≅Extn+i(E,M) for all i ≥ 1. By (2), cidM ≤ n, thus Extn+i(E,M)=0 and so Exti(E, C ) = 0 for all i ≥ 1. Hence C is strongly copure injective.

0 → M → E0→ E1→ … → En-1→ C → 0,

with C the n-th cosyzygy of M , applying Hom(E, -) with E an injective left (right) R-module, we get an isomorphism Exti(E, C )≌Extn+i(E, M) by dimension shifting for all i ≥ 1. By (3), C is strongly copure injective, so Exti(E, C ) = 0 and we get that Extn+i(E, M ) = 0. Hence pdE ≤ n. Therefore R is n-Gorenstein again by [2, Theorem 9.1.11(5)].

Similarly, we can define the copure flat dimension (cfd) of an R-module M,which is the largest positive integer n such that Torn(E, M ) ≠0 for all injective E. For an strongly copure flat module M , we set cfdM = 0.

We have the following Proposi-tion:

Proposition 2.7. Let R be a left and right noetherian ring and M a strongly copure flat R-module. The following are equivalent:

(1).R is n-Gorenstein;

(2).cfdM ≤ n for all left and right R-modules M ;

(3).If 0 → K → Pn-1→ … → P1→ P0→ M → 0 is an exact sequence of any left (right) R-module M with each Piprojective, then K is strongly copure flat.

Proof. It is similar to Proposition 2.6 and we omit the proof.

Acknowledgement The authors would like to express their sincere thanks to the referee for his or her careful reading of the manuscript and helpful suggestions.

This research was partially supported by the school level subject of ZiBo Normal College (the study of homology dimension with respect to semidualizing modules, No.14XK014).

[1]N.Q.Ding, J.L.Chen, On copure flat modules and flat resolvents, Comm. Algebra 24(1996), 1071 -1081.

[2]Enochs, E. E., Jenda, O. M. G. (2000). Relative homological algebra. Berlin, New York: De-Gruyter.

[3]E.E.Enochs,O.M.G.Jenda,Copure injective modules,Quaest.Math.14(1991),401-409.

[4]E.E.Enochs, O.M.G.Jenda, Copure injective resolutions, flat resolutions and dimen-sions, Comment. Math. 34 (1993), 203-201.

[5]G¨obel, R., Trlifaj, J. (2006). Approximations and Endomorphism Algebras of modules.Berlin, New York: De Gruyter.

[6]Holm, H., Gorenstein homological dimensions, J. Pure Appl. Algebra 189(1)(2004), 167-193.

[7]O.Jenda, On Gorenstein rings, Math. Z.197 (1988), 119-122.

[8]Holm, H., Jørgensen, P. Covers, precovers and purity, Illinois J. Math. 52(2)(2008), 691-703.

[9]R.Sazeedeh, Strongly torsionfree, copure flat and Matlis reflexive modules, J.Pure Appl. Algebra 192(2004), 265-274.

[10]Rada, J., Saor'n, M. Rings characterized by (pre)envelopes and (pre)covers of their modules, Comm.Algebra, 26(1998), 899-912.

[11]Salce, L. Cotorsion theories for abelian groups, Symp. Math., 23(1979), 11-32.

[12]White, D., Gorenstein projective dimension with respect to a semidualizing module. J. Commut. Algebra, 2(1)(2010), 111-137.

(责任编辑：胡安波)

Let R be an associative ring, M be a left and right R-module. M is called strongly copure injective if Exti(E, M ) = 0 for all injective module E and all i ≥ 1, copure injective if Ext1(E, M ) = 0. M is called strongly copure flat if Tori(E,M)=0 for all injective module E and all i ≥ 1, copure flat if Tor1(E,M)=0. We find the relation between the (strongly) copure injective and the (strongly) copure flat modules. Furthermore, we give the proof of some conclusions put forward by Enochs and Jenda in [2, Exercises 1,2,3].

copure injective module; copure flat module; (pre)covering; (pre)enveloping; cotorsion theory.

2016-01-01

张珍(1982-)，女，山东菏泽人，博士，淄博师范高等专科学校初等教育系教师，主要从事同调代数方向的研究。

注：本文为淄博师范专科学校校极课题“半对偶化模诱导的同调维数的研究”[14xk014]的阶段性研究成果。

理学研究

O151

A

(2016)02-0040-05