含Poisson跳线性随机系统区间稳定状态下的系统状态收敛速度分析
李 奇 勋
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
含Poisson跳线性随机系统区间稳定状态下的系统状态收敛速度分析
李 奇 勋
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
本文讨论了由布朗运动和Poisson跳跃过程共同驱动的随机线性时不变系统的区间稳定性问题.在引入广义李雅普诺夫算子的基础上,首先给出了含Poisson跳线性随机系统 (-β,-α)稳定的定义,然后结合谱分析方法分析了系统状态收敛速度与(-β,-α)稳定的关系,并得到了相关结论.
Poisson跳跃;区间稳定性;系统状态收敛速度
1 引言
稳定性是控制理论中的重要概念[1],是研究许多控制问题的必要前提,比如二次最优控制问题[2]、H2/H∞控制问题[3]等.对于动力系统的稳定性有着许多不同的描述,常见的有“渐近均方稳定”[4]、“弱稳定”[5]、“指数稳定”[6]等.众所周知,线性定常系统
(1)
渐近均方稳定当且仅当矩阵A的所有特征值位于左半复平面上.这种判别方法称为“特征值判据”,又叫“谱判据”.文献[4]发展这种方法到伊藤型线性随机系统中,即对于伊藤型线性随机系统
dx=Axdt+CxdWt,x(0)=x0∈Rn
(2)
构造广义李雅普诺夫算子

若算子Η的谱全部位于左半复平面上,则系统(2)渐近均方稳定.
简单的说,算子谱越往左,系统状态收敛的越快.有时为了保证系统具有良好的瞬态特性,如频域形式的增益稳定裕度和相位稳定裕度,需要系统的谱位于左半复平面的某一区间内,这就是区间稳定问题.文献[7]根据算子Η的谱定义了区间稳定性,在区间稳定性的约束下进行系统的性能分析更具广泛性、复杂性和工程意义.
本文将用算子谱的方法研究含Poisson跳线性随机系统中的一类区间稳定性问题,并对系统状态收敛速度进行分析.
符号描述:Sn(R)代表元素为实数的n×n对称矩阵集合,Rn×m代表元素为实数的n×m矩阵集合,Rn代表元素为实数的n维向量集合,AT代表A的转置矩阵,C表示复数域,C-表示复数域负半平面,I表示单位矩阵.
2 系统描述
设(Ω,F,G,P)为一完备概率空间,信息流G={Ft∶t≥0}由下面两个相互独立的随机过程生成:
1){Wt}t≥0为定义在该概率空间上的d维标准布朗运动;
2) 一个定义在R+×E上的泊松随机测度μ,其中E⊂Rl为非空开集,它的Borel域为B(E),它的补偿因子为

对于所有满足λ(A)<∞的A∈B(E)是鞅.λ假定为(E,B(E))上的σ-有限lévy测度,相应的过程称为泊松过程.
本文讨论的是由布朗运动和泊松跳跃过程共同驱动的线性随机自治系统:
(3)
为方便,本文将x(t),y(t)皆简写为x,y.其中x(t)∈Rn,y(t)∈Rl分别为系统状态和量测输出,(A,A0,A1(e),Q)∈Rn×n×Rn×n×Rn×n×Rl×n,A,B,A0,B0,A1(e),B1(e) 是系统参数,Q是输出矩阵.
3 区间稳定与系统状态收敛速度
受文献[4]启发,我们定义一个李雅普诺夫算子Η如下:

且算子的谱σ(Η)∶={λ∈C∶Η(X)=λX,X≠0} .
下面我们通过算子谱定义一类区间稳定:(-β,-α) 稳定.

注1 显然,渐近均方稳定是(-β,-α)稳定的一种特殊形式.即,若系统(3)是(-β,-α)稳定的,则系统(3)一定是渐近均方稳定的.
下面我们使用算子谱技术,对系统(3)在(-β,-α)稳定情况下系统状态收敛速度进行分析.
定理1 假设系统(1)是(-β,-α)稳定的,则系统(3)是渐近均方稳定的,且系统状态收敛的速度比e-αt快,比e-βt慢.即存在常数C1和C2,使得
C1e-βt≤E‖x(t)‖2≤C2e-αt.
证明 我们记
max(Re(λi))=λ1,min(Re(λi))=λn(n+1)/2.
其中λi∈σ(Η),i=1,2,…,n(n+1)/2.
令
X(t)=E[x(t)xT(t)],
使用伊藤公式可以得到:
(4)
方程(4)是n×n对称矩阵方程,且X∈Sn(R).所以方程(4)实质上可以等价于一个n(n+1)/2阶向量方程.即存在唯一n(n+1)/2×n(n+1)/2矩阵L,使得:



容易证得σ(L)=σ(Η),所以λ1,λn(n+1)/2也分别为矩阵L最大、最小特征值.不失一般性,假设λ1,λn(n+1)/2所表示的值分别为矩阵L的p,q重特征值.
由常微分方程理论可以知道,存在常数C3和C4使得:

(5)
令x=(x1,x2,…,xn)T,xT=(x1,x2,…,xn) ,则



同时
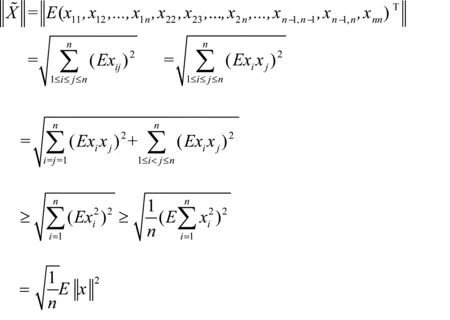
即

综上所述,我们得到

(6)
变形得

(7)
因为Re(λ1)<-α、Re(λn(n+1)/2) >-β,所以
Re(λ1)-α<0,Re(λn(n+1)/2) -β>0.即e[Re(λ1)-α]t≤1,e[Re(λn(n+1)/2)-β]t≥1,t∈[0,+∞).
联立(5)、(6)、(7)式,可得


令

便得

4 结论
在这篇文章中,我们借助算子谱技术研究了由泊松随机过程和布朗运动共同驱动的线性随机系统的区间稳定性.本文在定义(-β,-α)稳定的基础上,证明了若系统是(-β,-α)稳定的,则系统状态收敛速度e-αt快,比e-βt慢.
[1]刘豹,唐万生.现代控制理论[M].北京: 机械工业出版杜, 2015.
[2]Rami M A, Zhou X Y. Linear matrix inequalities, Riccati equations, and indefinite stochastic linear quadratic controls[J].IEEE Transactions on Automatic Control,2000,45(6):1131-1143.
[3]Lin X, Zhang R. H∞control for stochastic systems with Poisson jumps[J].Journal of Systems Science and Complexity,2011,24(4):683-700.
[4]Zhang W, Chen B S. On stabilizability and exact observability of stochastic systems with their applications[J].Automatica,2004,40(1):87-94.
[5]Zhang W, Zhang H, Chen B S. Generalized Lyapunov equation approach to state-dependent stochastic stabilization/detectability criterion[J]. IEEE Transactions on Automatic Control,2008,53(7):1630-1642.
[6]Hu L, Mao X. Almost sure exponential stabilisation of stochastic systems by state-feedback control[J].Automatica,2008,44(2):465-471.
[7]Zhang W, Xie L. Interval Stability and Stabilization of Linear Stochastic Systems[J].IEEE Transactions on Automatic Control,2009,54(4):810-815.
Some Relationships among the Interval Stability and the Convergence Rate of System State of Poisson Jumps Systems
LI Qi-xun
(School of Mathematics and Systems Science, Shandong University of Science and Technology, Qingdao, 266590, China)
This paper discusses interval stability of stochastic linear time invariant systems driven by Brownian motion and Poisson jumps process. Based on introducing the generalized Lyapunov operators, firstly, the definition of (-β,-α)-stability of stochastic systems with Poisson jumps is defined. Then combined with the spectrum analysis method, relationships among the system state convergence rate and (-β,-α)-stability are analyzed, and the conclusion is obtained.
Poisson jumps; interval stability; convergence rate of system state
2016-10-07
李奇勋(1992-),男,山东济宁人,山东科技大学数学与系统科学学院硕士研究生.
O211
A
1672-2590(2016)06-0047-05

