WSB曲线的升阶公式和递推算法
唐桂林,陈明武,金京犬
(安徽邮电职业技术学院 计算机系,安徽 合肥 230031)
WSB曲线的升阶公式和递推算法
唐桂林,陈明武,金京犬
(安徽邮电职业技术学院 计算机系,安徽 合肥 230031)
WSB曲线通过引入参数L、u来表示Bezier曲线、Wang-Ball曲线、Said-Ball曲线以及它们之间的中间曲线.利用WSB函数的对偶泛函给出WSB型曲线的升阶公式和递推算法.通过升阶公式可以提高WSB型函数的次数,通过递推算法可以实现WSB曲线和Said-Ball型曲线、Bezier曲线的转换.此算法在计算机辅助几何设计理论研究和实际应用中都有一定的意义.
计算机辅助几何设计;WSB曲线;对偶基;升阶公式;递推算法
0 引言
Ball于1974年首次提出三次Ball基函数[1-2],之后王国瑾提出了Wang-Ball曲线[3].与此同时Said也提出了Said-Ball曲线.Wang-Ball曲线和Said-Ball曲线在曲线的稳定性、对称性、端点插值性、几何不变性等性质十分相似.Bezier曲线通过各个节点控制曲线的形状明显优于Ball曲线、Wang-Ball曲线和Said-Ball曲线.在实际应用中,WSB曲线[4]对Bezier曲线、Wang-Ball曲线、Said-Ball曲线进行了统一,这在理论研究和实际应用中都具有重要意义.
利用WSB基函数的对偶基,再结合Bezier曲线的de Caste算法、Wang-Ball曲线和Said-Ball曲线的升阶逼近算法,推导出WSB曲线的升阶递推算法,同时利用WSB函数对偶泛函得到WSB的升阶 公式.
1 WSB曲线
定义1[4]给定R2或R3中n+1个控制点,对于给定的整数0≤u≤m-L+1,0≤L≤m,称曲线为n次Wang-Said-Bezier型曲线,0≤t≤1,如图1所示.称为WSB基函数.

图1 L,u取不同值时的7次WSB曲线

2 WSB基函数的对偶基
当n=2m+1时,WSB基函数的对偶基为:

当n=2m时,WSB基函数的对偶基为:
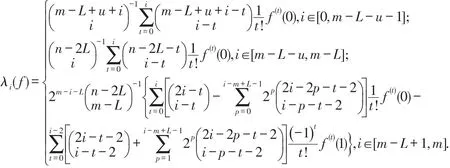

3 WSB曲线的升阶公式

4 WSB曲线的递推算法
将Wang-Ball曲线、Said-Ball曲线的求值算法与Bezier曲线的de Caste算法综合在一起就可以得到下列算法:
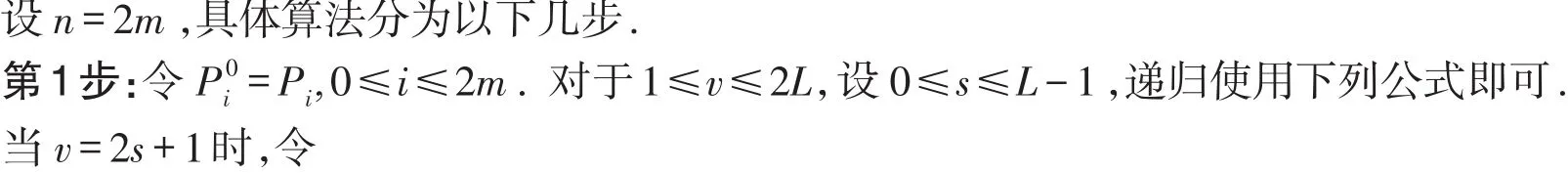

5 结论
用对偶泛函(基)来研究WSB基函数是解决各类多项式基转换到WSB基的根本方法.本文利用WSB对偶泛函把n次WSB曲线升阶为n+1次WSB曲线,利用本文所给的递推算法得到了2m-2L次Said-Ball曲线和m-L+u+1次Bezier曲线;再利用关于Bezier曲线求值的de Caste算法,便得到了2m次曲线.
[1]BALL A A.Introduction of the conic lofting tile part 1[J].Computer-aided Design,1974,6(4):243-246.
[2]BALL A A.Describe of the algorithm part 2[J].Computer-aided Design,1975,7(4):237-242.
[3]王国瑾.高次Ball曲线及其应用[J].高校应用数学学报,1987,2(1):126-140.
[4]汪志华,朱晓临.Bezier曲线与两类广义Ball曲线的统一表示[C]//第四届全国几何设计与计算学术会议,2009:13-16.
[5]缪永伟.Poisson曲线的升阶算法[J].工程图学学报,2003(4):78-82.
[6]任民宏.应用Casteljau算法绘制Bezier曲面[J].陕西理工学院学报(自然科学版),2007,23(2):22-24.
[7]韩丽娜,张红祥.Bezier曲线修改的一种分割算法[J].计算机工程与科学,2006,28(7):77-79.
The Degree Elevation Formula and Recursion Method for the WSB Curves
TANG Guilin,CHEN Mingwu,JIN Jingquan
(Department of Computer Technology,Anhui Post and Telecommunication College,230031,Hefei,Anhui,China)
With the different parameters of L and u,WSB curves represented a number of useful curves with the uniform expression.Bezier curves、Wang-Ball curves and Said-Ball curves are a special case of WSB-type curve.By using dual function,the degree elevation forula and recursion method about WSB curves are given.We can improve the number about the function of the WSB,implement conversion between the Bezier curves,Wang-Ball curves and Said-Ball curves by the recursion method about WSB curves.The algorithm has certain significance in the theoretical research and practical application about the computer aided geomet⁃ric design.
CAGD;WSB curves;dual basis;degree elevation forula;recursion method
TP 391
A
2095-0691(2016)04-0022-04
2016-09-06
安徽省高校自然科学基金项目(KJ2016A382);安徽省省级质量工程项目(2015jyxm651)
唐桂林(1984- ),男,安徽宿松人,讲师,研究方向为计算机辅助几何设计、插值、偏微分方程.

