双转子径向永磁电机定子支撑结构刚度分析

高 俊，孙晓明 ，张 宇，佟文明，安忠良

(1.沈阳工业大学 国家稀土永磁电机工程技术研究中心,沈阳 110870; 2.沈阳鼓风机通风设备有限责任公司,沈阳 110022;3.辽宁省电力有限公司检修分公司，沈阳 110003)



双转子径向永磁电机定子支撑结构刚度分析

高 俊1，孙晓明2，张 宇3，佟文明1，安忠良1

(1.沈阳工业大学 国家稀土永磁电机工程技术研究中心,沈阳 110870; 2.沈阳鼓风机通风设备有限责任公司,沈阳 110022;3.辽宁省电力有限公司检修分公司，沈阳 110003)

双转子径向永磁电机能够有效利用电机内部空间，提高电机的转矩密度。但目前国内外对双转子永磁电机的研究仅停留在研究试制阶段，对双转子电机结构方面的研究甚少，其中涉及大功率双转子永磁电机结构的研究还不是很深入。针对双转子电机的结构特点，提出了一种适用于大型永磁风力发电机的定子双支撑式双转子永磁电机结构，并对该结构的定子支撑结构进行了理论分析，推导出了定子支撑结构的刚度解析公式，以一台1.65 MW，150 r/min的双支撑式双转子永磁风力为例，利用有限元方法验证了解析公式的正确性。

双转子径向永磁电机；定子双支撑；定子支撑结构；刚度分析

0 引 言

双转子、单定子径向永磁电机与普通结构电机相比，双转子结构能够有效利用电机内部空间，可以提高电机的转矩密度。但目前国内外对双转子永磁电机的研究仅停留在研究试制阶段，所研究电机的功率较低，而且大多研究均为电磁方面，对双转子电机结构方面的研究甚少，其中涉及大功率双转子永磁电机结构的研究还不是很深入。

美国威斯康辛大学设计了一台2.2 kW的小型双转子永磁电机，提出了一种金属框架式的结构固定方式，但仅为初步设计，而且该框架的结构强度较差，不适用于大型电机结构[1-3]。文献[4-5]仅对双转子电机的气隙磁密分布变化等进行了有限元分析研究；文献[6-9]主要研究异向旋转的双转子电机理论；文献[10-11]对小功率双转子永磁电机进行了理论公式推导及减少齿槽转矩方法的研究；文献[12]对双转子永磁风力发电机进行了理论公式推导，并设计了一台1.65 MW的双转子永磁风力发电机，但未对该电机结构进行分析研究。

本文在此研究基础上，针对双转子电机的结构特点，提出了一种定子双支撑式双转子永磁风力发电机结构，并对该结构的定子支撑部分进行了理论分析，推导出了定子支撑结构的刚度解析计算公式。最后以一台1.65 MW，150 r/min的双支撑式双转子永磁风力为例，利用有限元方法验证了解析公式的正确性。

1 结构模型

双转子、单定子径向永磁电机，在结构上存在内、外两个转子，定子铁心位于内、外转子之间，形成两个气隙，本文称之为内气隙g1和外气隙g2，共同构成电机能量转换的枢纽，也提高了电机的转矩密度，但于此同时是也对双转子电机造成了负面影响，如直接影响气隙均匀度，造成内、外气隙值相差很大，严重时会发生扫堂，而产生这种不良影响的主要原因：(1)该结构一个定子铁心需要同时与内、外两个转子进行能量交换，定子部分需要应用更多的铁磁材料，故其重量较常规电机重30%～50%，由重力产生的内、外转子偏心量也会随之增大。(2)该结构中外转子部分必须采用单臂支撑结构，刚度较差。

本文针对上述问题提出一种定子双支撑式双转子永磁风力发电机结构，其结构如图1所述，其三维结构如图2所示。

图1 双支撑式双转子永磁风力发电机平面示意图

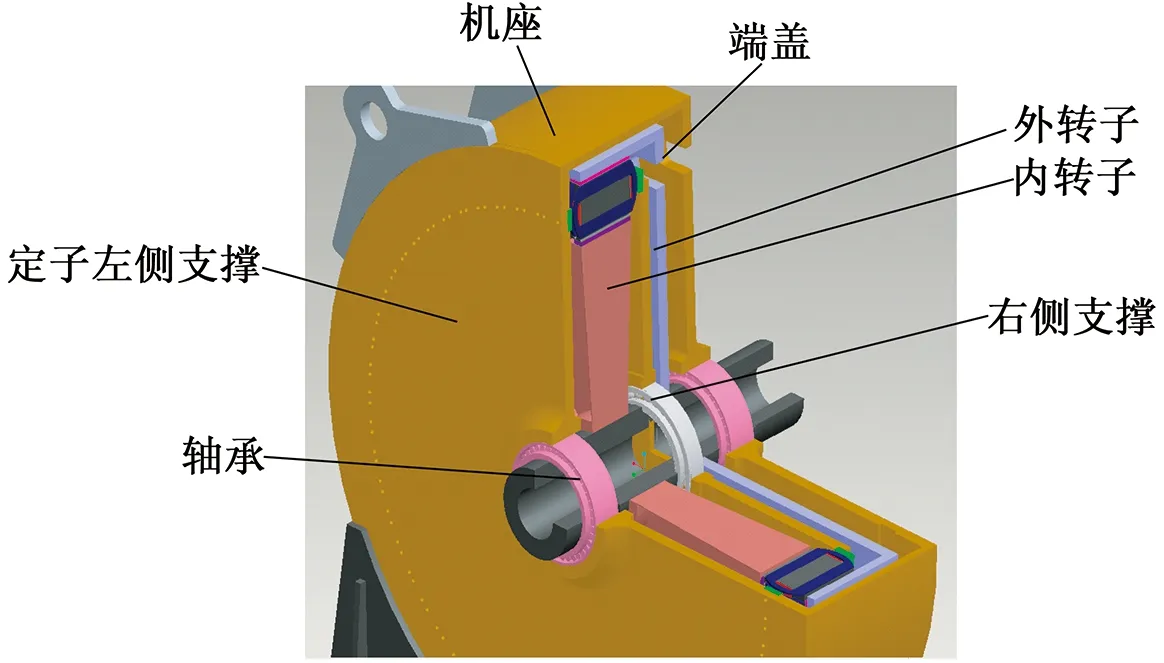
图2 双支撑式双转子永磁风力发电机三维结构图

如图1所示，双转子永磁发电机可看成一台外转子永磁发电机与一台内转子永磁发电机套在一起，并共用一个定子铁心的新型电机。该电机内外转子通过转轴同步旋转。定子铁心一端固定在定子左侧支撑端面上，另一端固定在定子右左侧支撑端面上，定子左侧、右侧支撑通过横穿定子铁心的支撑杆联接，与此同时与轴承、转轴建立良好的同轴度关系，以保证定、转子之间的同轴度要求。

2 定子铁心刚度分析

由于该电机的定子铁心经由支撑杆同两侧的定子支撑联接，即定子铁心的自重及所受外载荷均有支撑杆承担，支撑杆的变形是引起定子偏心的主要原因，故需对支撑杆进行刚度的分析，以保证电机的正常运行。

该双转子电机定子支撑杆结构的受力模型，如图3所示。

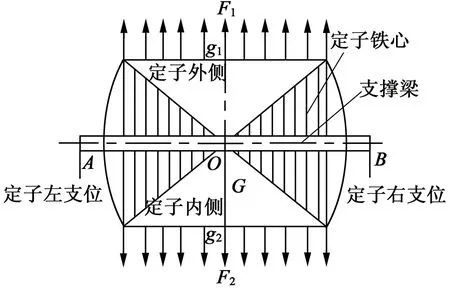
图3 定子支撑结构受力模型

由图3可知，定子铁心主要受到三个载荷的作用，即外转子与定子间的磁拉力F1、内转子与定子间的磁拉力F2和定子铁心的重力G。

在上述载荷的综合作用下，支撑杆将发生弯曲，根据材料力学对其进行，力学图解分析，如图4所示。

图4 力学图解

根据图5列出支撑杆的力学平衡方程如下:

由于该支撑杆的A端、B端均固定，故yA，θA，yB，θB为零，所以可得:

而当力作用于支撑杆的中央时，由于对称，最大偏心发生于杆的中点，即a=l/2处，带入式(6)可得双转子电机定子支撑杆最大挠度计算公式:

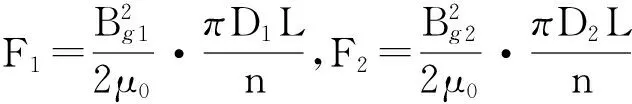
式中:L为定子铁心长；E为弹性模量；I为支撑杆的截面惯性矩；n为支撑杆的数量；D2为定子铁心外径；D1为定子铁心内径；Bg2为内气隙磁密最大值；Bg1为外气隙磁密最大值；l为支撑杆长度。

3 双转子永磁电机定子结构分析实例

本文研究的电机为1.65 MW双转子半直趋永磁风力发电机，计算例中电机基本计算参数如表1所示。由自身重力G产生的支撑杆变形量及定子铁心变形量有限元计算结果如图5～图6所示。由磁拉力F1和F2作用产生的支撑杆变形量及定子铁心变形量有限元计算结果如图7～图8所示。由自身重力和磁拉力产生的支撑杆变形量及定子铁心变形量如图9～图10所示。

定子支撑杆变形量解析法与有限元法计算结果比较，如图11～图13所示。

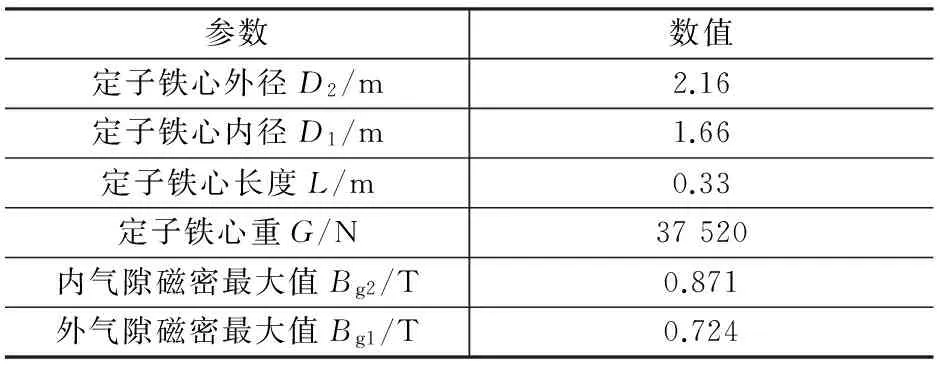
表1 算例定子主要参数

图5 由重力G产生的支撑杆变形

图6 由重力G产生的定子铁心变形

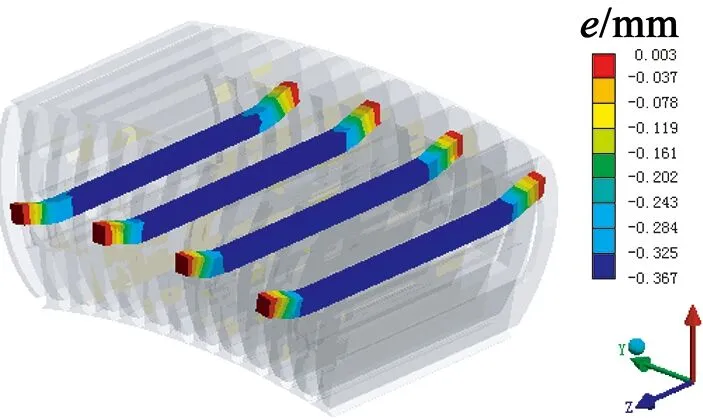
图7 由磁拉力产生的支撑杆变形

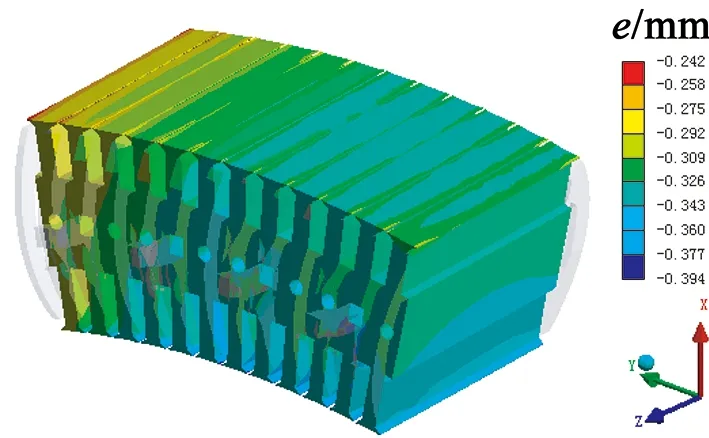
图8 由磁拉力产生的支撑杆变形

图9 由合力产生的支撑杆变形

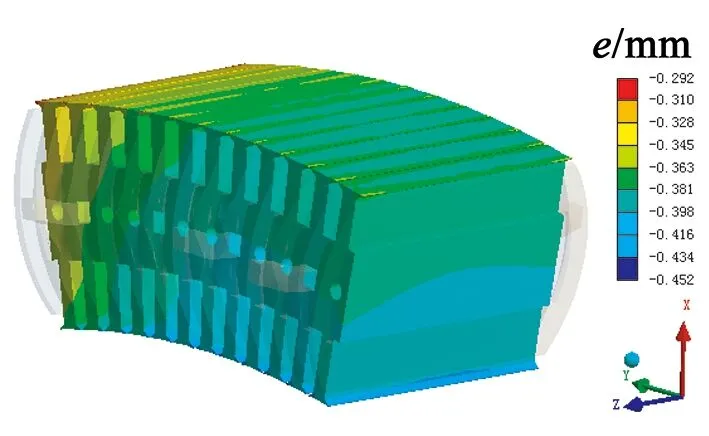
图10 由合力产生的定子铁心变形

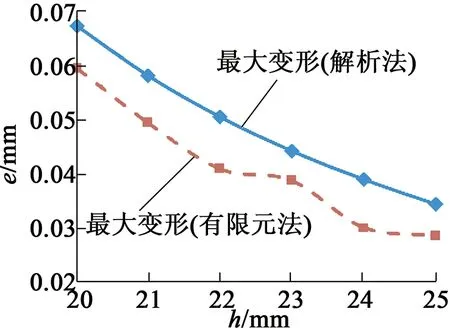
图11 由重力产生支撑杆变形分析对比

图12 由磁拉力产生支撑杆变形分析对比

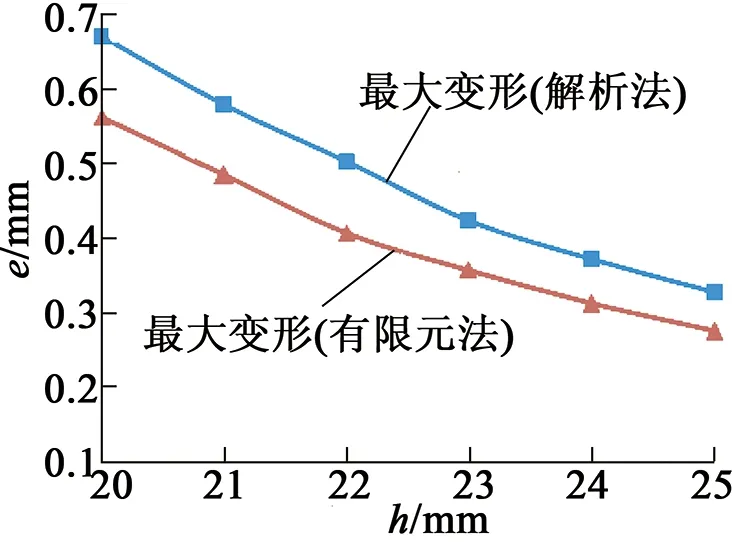
图13 由合力产生支撑杆变形分析对比

由图5、图7、图9可知，定子支撑杆由定子铁心及自身重力G产生的最大变形为0.040 8 mm，而由磁拉力F1和F2产生的最大变形达到了0.367 mm，由两者合力产生的变形为0.407 mm。支撑杆两侧固定，故最大变形位置为支撑杆的中间段。而且由于定子铁心与支撑杆为紧密配合，故支撑杆将受到定子铁心的约束，所以支撑杆产生的变形不是正弦的挠变形，而是梯形的挠变形，即支撑杆与定子铁心配合段产生的变形一致。

由图5～图10可知，定子支撑杆产生的变形与定子铁心产生的变形量计算结果相近；考虑定子铁心的变形时，不仅要考虑重力G，磁拉力F1，F2产生的支撑杆变形对定子铁心影响，还要考虑磁拉力F1，F2对定子铁心表面的作用，故定子铁心产生的变形应比支撑杆产生变形稍大，由计算结果可以看出该值大了8%左右。

图11～图13中，对定子支撑杆最大变形量进行了有限元法和解析法的分析对比。由对比可知，支撑杆最大变形量的解析法计值稍大于有限元法计算值，相差10%左右。分析解析法计算值稍大的原因为解析法在计算时没有考虑到定子铁心对支撑杆变形的约束作用，故计算值稍大。

4 结 语

本文提出了一种定子双支撑式双转子永磁风力发电机结构，并对该结构的定子支撑部分的刚度进行了理论分析。通过以一台1.65 MW，150 r/min双转子电机的定子部分刚度分析为例，得到以下结论:

1) 对于双支撑式双转子永磁电机定子部分的刚度主要受自身重力和内、外磁拉力的影响，其中磁拉力对刚度的影响占主要作用。

2) 考虑到磁拉力对定子铁心内、外表面的作用，故定子铁心产生的最大变形稍大于支撑杆产生的最大变形，相差8%左右。由于支撑杆结构简单，易于进行解析法计算，故在考虑定子铁心变形时，可先对支撑杆进行计算，然后进行适当修正。

3) 由于有限元计算时能考虑定子铁心对支撑杆变形的约束作用，计算值更为准确，支撑杆变形量的有限元法计算值小于解析法计算值10%左右。

[1] QU Ronghai,LIPO T A.Design and parameter effect analysis of dual-rotor, radial-flux,toroidally-wound,permanent-magnet machines[J].Transactions on industry applications,2004,40(3):771-779.

[2] QU Ronghai,LIPO T A.Dual-rotor,radial-flux,toroidally-wound,permanent-magnet machine [J].IEEE Transactions on Industry Applications,2003,39 (6):1665-1673.

[3] QU Ronghai,LIPO T A.Design and optimization of dual-rotor,radial-flux,toroidally-wound,permanent - magnet machine[C]//Industry Applications Conference，IAS Meeting.2003:1397-1404.

[4] 曹江华,杨向宇,肖如晶.双转子径向永磁电机气隙磁密的分析计算[J].微电机,2010,43(8):28-31.

[5] 曹江华,杨向宇,肖如晶.双转子径向永磁电机设计与有限元分析[J].电机与控制应用,2010,37(1)：8-12.

[6] 刘光伟.异向旋转双转子永磁同步电机基础理论分析与仿真研究[D].沈阳:沈阳工业大学,2008.

[7] 张凤阁.对转双转子永磁同步电动机电枢电抗的有限元计算[J].电气技术,2009(4):32-36.

[8] 张凤阁,刘光伟,陈进华.异向旋转双机械口永磁电机磁路建模与场分析[J].电机与控制学报,2009,13 (6):804-810.

[9] 白旭华.新型内外双转子感应电动机研究[D].沈阳:沈阳工业大学,2005.

[10] 王正平.径向磁场双转子永磁电机研究[D].济南:山东大学,2006.

[11] 王法庆.双转子永磁风力发电机研究[D].济南:山东大学,2007.

[12] 褚占宇，安忠良，佟文明，等.双转子永磁风力发电机设计[J].电工技术学报,2013,28(S1):265-270.

Stator Support Structure Stiffness Analysis of Dual-Rotor Permanent Magnet Machine

GAOJun1，SUNXiao-ming2，ZHANGYu3，TONGWen-ming1，ANZhong-liang1

(1.Shenyang University of Technology,National Engineering Research Center for Rare-Earth Permanent Magnet Machines,Shenyang 110870,China; 2.Shenyang Blower Works Group Co., Ltd.,Shenyang 110022,China; 3.China Maintenance Branch of State Grid Liaoning Electric Power Company，Shenyang 110003,China)

Dual-rotor radial permanent magnet machine can utilize the volume effectively, and improve the torque density.Currently, the study of Dual-rotor radial permanent magnet machine is still in the trial stage, and little study focus on the structure of the machine, especially about the large power of machine.Based on the structure of dual-rotor machine, a stator support structure was proposed to improve the stiffness of large power wind permanent magnet machine.Theory analysis was developed about the support structure, and derived the analytic formula.Based on the dual-rotor permanent magnet machine rated at 1.65 MW, 150 r/min, the analytic formula was verified by finite element method.

dual-rotor radial permanent magnet machine; stator double support; stator support structure; stiffness analysis

2016-03-04

TM351

A

1004-7018(2016)09-0036-04

高俊(1984-)，男，硕士，工程师，研究方向为永磁电机设计及其结构工艺。