分布式嵌套阵列及其DOA估计*

谢玉凤，白 媛，马秀荣

(1.天津理工大学 计算机与通信工程学院，天津 300384；2.桂林电子科技大学，桂林 541004)



分布式嵌套阵列及其DOA估计*

谢玉凤**1,2，白 媛1,2，马秀荣1

(1.天津理工大学 计算机与通信工程学院，天津 300384；2.桂林电子科技大学，桂林 541004)

提出了一种分布式嵌套阵列天线结构，由两个相互独立的四级嵌套子阵构成。两个子阵间存在一个基线长度，且满足一定条件。对该阵列天线接收到的信号进行高阶累积量和Khatri-Rao积运算可以得到三个完全相同的均匀直线阵列天线结构。针对新得到的阵列天线结构，使用基于空间平滑技术的双尺度酉旋转不变子空间(ESPRIT)波达方向(DOA)估计算法对信号进行DOA估计。该方法可以有效地提高阵列天线的自由度，进而达到提高估计精度的目地。仿真结果证明了基于所提出阵列天线结构的DOA估计方法的有效性。

分布式嵌套阵列；高阶累积量；均匀直线阵列；波达方向估计

1 引 言

在过去的20年里，很多基于高阶累积量的阵列处理方法[1-2]迅速发展用来估计非高斯信源的波达方向(Direction of Arrival，DOA)。其中，最典型的算法是基于四阶累积量的DOA估计算法[3-5]。与二阶统计量的DOA估计算法相比，基于四阶累积量的DOA估计算法可以很好地抑制高斯噪声，提高DOA估计的精度，形成大量的虚拟阵元，扩大阵列天线的孔径，因此增加了可以估计的非高斯信号的数目，并且该数目大于物理阵元的数目。该问题也就是现阶段DOA估计改进算法中所要解决的欠定问题。

阵列孔径是影响波达方向估计精度的重要因素，但阵列孔径的加大将会提高硬件成本。为了有效解决以上问题，稀疏布阵的方式被广泛应用。稀疏布阵的最大优势是不仅可以保持原有阵列天线的阵列孔径，而且还可以提高阵列的分辨率，降低硬件成本。但其不足之处是当阵列基线大于半波长时，波达方向估计模糊问题[6-7]便会随之而出。为了解决估计模糊的问题，文献[8-9]提出一种分布式均匀线阵(Uniform Linear Array，ULA)，使用双尺度酉旋转不变子空间算法(Estimation of Signal Parameters via Rotational Invariance Techniques，ESPRIT)对其进行解模糊处理，并且对信号进行波达方向估计。但是此方法的最大缺点是得到的阵列天线的自由度大大降低，因此使得可估计的信号数目少于子阵物理阵元数目。为了估计出更多的信号数，需要使用更多的阵元，这将会无形地增加技术难度和经济成本。因此，2010年，文献[10-12]提出了一种嵌套阵列天线结构，大大增加了阵列天线的自由度。基于这种结构相应的波达方向估计方法也随之产生，在信号数大于物理阵元数的情况下，该方法可以实现对信号的有效波达方向估计，并且提高了信号的估计精度。

本文提出了一种新的稀疏阵列天线结构，即分布式嵌套阵列天线结构。该阵列天线结构将两个相互独立的四级嵌套阵列做为子阵，用来弥补均匀线阵分布式阵列自由度低的缺陷。对该阵列天线接收到的信号进行高阶累积量和Khatri-Rao积运算，得到3个完全相同的均匀直线阵列天线结构，大大提高了阵列自由度，进而提高了阵列分辨率。最后，由前两个均匀直线阵列天线结构与后两个均匀直线阵列天线结构之间的空间旋转不变性产生模糊的高精度估计，由第一个阵列天线结构与最后一个阵列天线结构之间的空间旋转不变性产生无模糊的粗估计，利用无模糊的粗估计对模糊的高精度估计进行解模糊处理，得到无模糊的高精度估计。与均匀线阵分布式阵列相比，该阵列可以估计出更多的非高斯信号源。仿真结果验证了以上结论。

2 信号模型

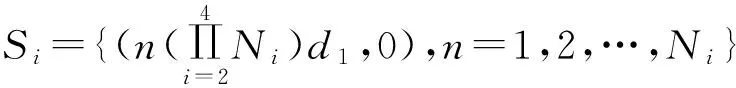
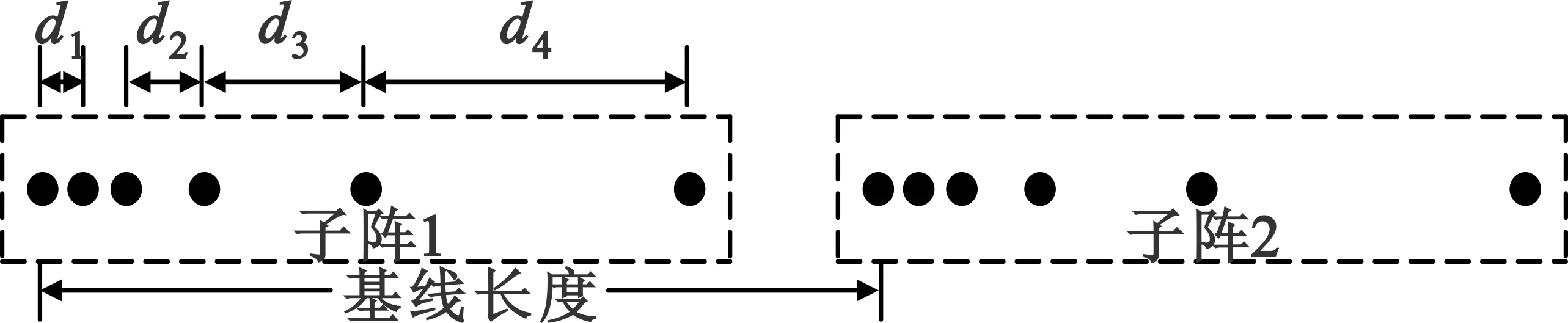
图1 分布式嵌套阵列

Fig.1Thedistributednestedarray

两个嵌套子阵的构造方式完全相同，且均为四级嵌套阵列结构，即子阵中各阵元间的距离满足四级嵌套阵列中各阵元距离的要求。两个子阵间的基线长度用B来表示，且B满足条件B>>λ/2，则整个阵列的接收信号为

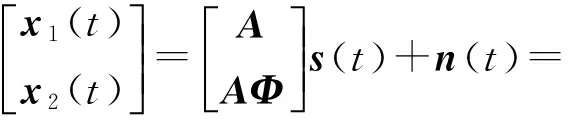
(1)

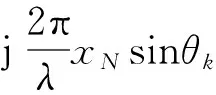
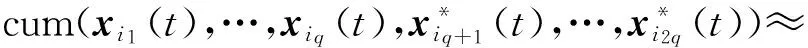
(2)

式中：C2q,x(l)是所述物理阵列天线结构第ik个阵元的接收信号，1≤ik≤N，1≤k≤2q；l是方向索引参数，可以为任意正整数；“⊗”表示Kronecker积;q=1,2,3,…为阶数的参数,当q>1时为高阶;ad⊗l(d=1,2,…,D)表示l个ad进行Kronecker积运算;σ2为噪声功率;INq×Nq为Nq×Nq维单位矩阵;δ(·)为狄拉克函数。

将式(2)中的高阶累积量矩阵C2q,x(l)进行向量化，因为当q>1时，δ(·)=0，因此可得到

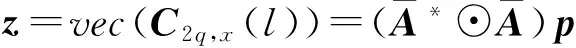
(3)

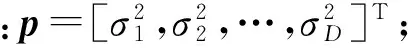
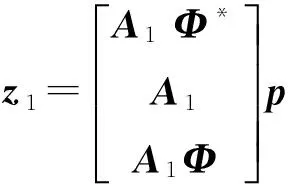
(4)

为了方便说明，令

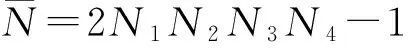
(5)

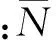
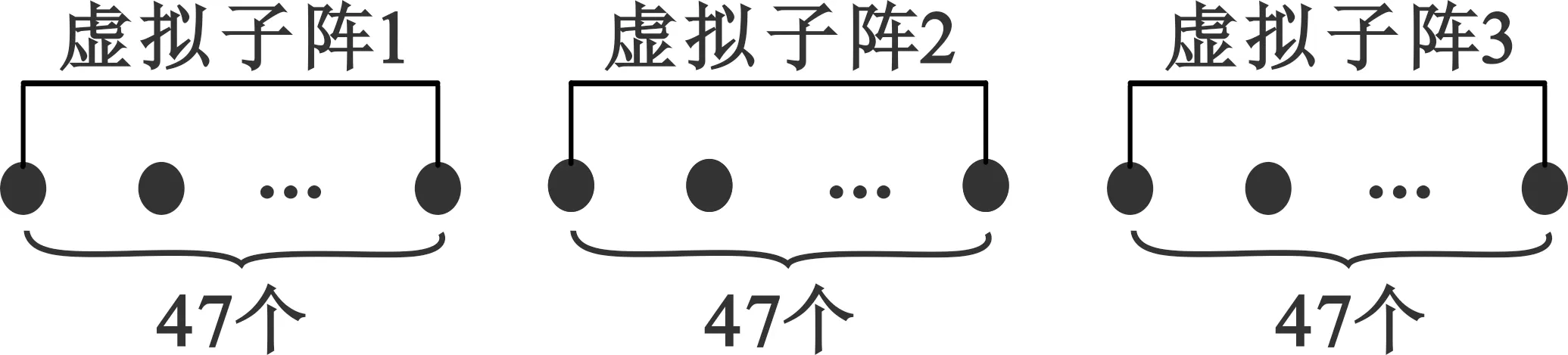
图2 形成的虚拟阵列

Fig.2 The formed virtual array

3 DOA估计算法

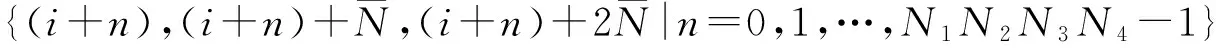
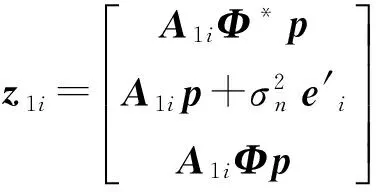
(6)

式中：A1i是矩阵A1中第i行到N1N2N3N4+i-1行的元素组成，其维数为(N1N2N3N4)×D；e′i是一个列向量，该列向量的第N1N2N3N4+i-1个元素为1，其他元素均为0。

第i个子阵接收数据的自相关函数Ri为

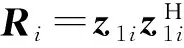
(7)

求出N1N2N3N4个Ri后，对其进行取平均值运算，则平滑后的协方差矩阵可以表示为

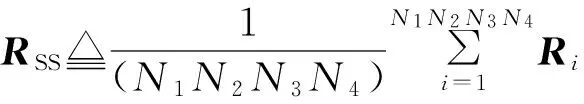
(8)

平滑后的ULA子阵阵元数为NSS=N1N2N3N4。

首先由于得到的ULA伴随阵列的平滑是关于中心对称进行的，并且其本身也具有中心对称性，因此，整个阵列天线最左边NSS-1列和最右边NSS-1列具有旋转不变性。这满足了使用双尺度酉ESPRIT算法的第一个前提条件。然后将3个ULA分为两组阵列，第一组阵列为前两个ULA，第二组阵列为后两个ULA，第1组阵列与第2组阵列之间具有一定的距离，也具有旋转不变性，由此，该阵列满足了使用双尺度酉ESPRIT算法进行波达方向估计的两个前提条件。平滑后的导向矢量可表示为

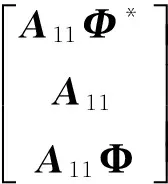
(9)

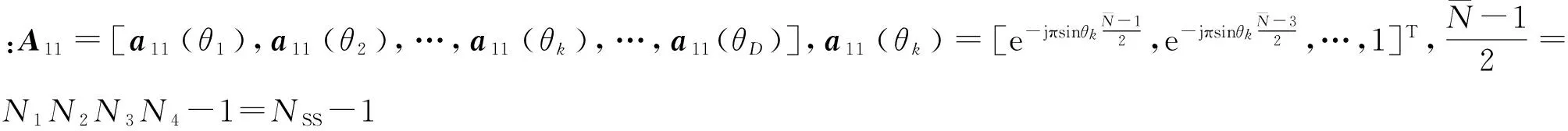
由此得到每个平滑子阵的阵元数目为NSS。利用双尺度酉ESPRIT算法对来波信号进行波达方向估计，最多可以准确估计出的信号数目由第一组阵列和第二组阵列中的阵元数决定。分布式ULA阵列天线结构最多可估计出的信号数为N，而分布式嵌套阵列天线结构最多可估计的信号数为2NSS=N2/2+N，显然，最多可估计出的信号数目增加了2NSS-N=N2/2个。

为了降低运算的复杂度，并且提高估计的分辨率，将RSS映射到实值空间，并对其进行特征值分解运算，可以得到

(10)

式中：ES表示信号子空间;ΛS表示由信号特征值所构成的对角矩阵；Q为酉矩阵；J为置换矩阵。

平滑后整个阵列天线结构除了中间NSS-1列外，其两边的NSS-1列之间的空间旋转不变性可以表示为

Φ1Jc1ASS=Jc2ASS。

(11)

式中：Jc1=I3⊗[INSS-10(NSS-1)×1]和Jc2=I3⊗[0(NSS-1)×1INSS-1]为选择矩阵；Φ1=diag(ejπsinθ1,ejπsinθ2,…,ejπsinθD)。

同理，两组阵列天线之间具有空间旋转不变性，其数学模型表示为

ΦJf1ASS=Jf2ASS。

(12)

式中：Jf1=[I2NSS02NSS×NSS]；Jf2=[02NSS×NSSI2NSS]。

最后，利用双尺度酉ESPRIT算法对信号进行波达方向估计。首先由两组阵列天线结构之间的空间旋转不变性产生模糊的高精度估计，然后由整个阵列天线结构除了中间NSS-1列外，其两边的NSS-1列之间的空间旋转不变性产生无模糊的粗估计，最后利用无模糊的粗估计对模糊的高精度估计进行解模糊处理，得到无模糊的高精度估计。

4 仿真与分析

仿真实验中，两个四级嵌套子阵均由6个阵元构成，每个四级嵌套子阵中第一级阵元间的距离d1=λ/2，基线长度B=24λ，快拍数N=1 000，独立的蒙特卡洛试验次数为p=600。均方根误差(Root Mean Square Error,RMSE)定义为

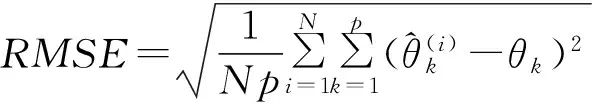
(13)

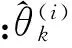
仿真14个完全独立的非高斯信号从(θ1,θ2,θ3,θ4)=(25°,50°,86°,120°)方向入射到分布式嵌套阵列天线上，信噪比(Signal-to-Noise Ratio,SNR)从-6～14 dB变化。图3为RMSE与SNR的曲线图。

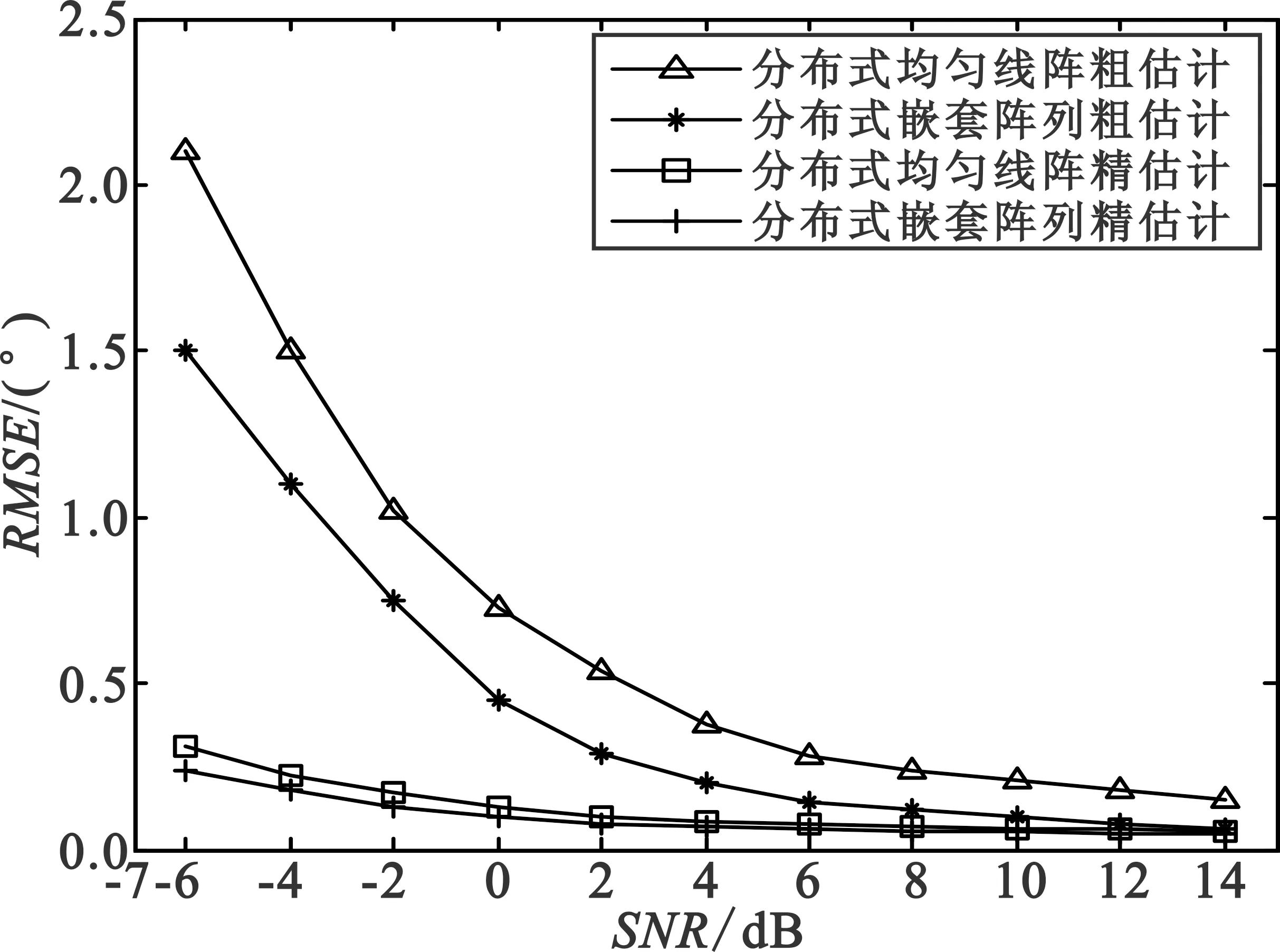
图3 RMSE与SNR的关系曲线

Fig.3 RMSE curves of DOA estimation versus input SNR

从图3可以看出，在相同信噪比情况下，分布式嵌套阵列精估计与分布式嵌套阵列粗估计相比明显提高了估计精度，且其估计精度优于分布式均匀线阵。当SNR=6 dB时，分布式嵌套阵列粗估计比分布式均匀线阵粗估计的估计误差低约0.2°,产生这种结果的原因是当物理阵元数相同时，嵌套阵列可以大大增加阵列的自由度，进而提高估计精度。

仿真2信号与仿真1相同，信噪比从-30～5 dB范围内变化。图4为检测概率与信噪比的曲线图。

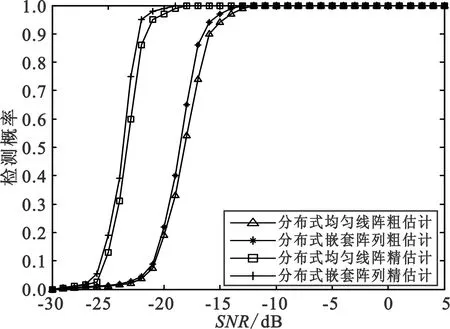
图4 检测概率与SNR的关系曲线

Fig.4 The probability of detection curves of DOA estimation versus input SNR

从图4可以看，当SNR=-20 dB时，分布式嵌套阵列便可以成功地检测出信号，而分布式均匀线阵需要当SNR=-14 dB时方可成功检测出信号,与分布式嵌套阵列相比降低了6 dB。产生这种结果的主要原因是嵌套子阵可以充分地利用形成的虚拟阵元，因此性能得到了明显提高。

仿真3两个完全独立的非高斯信号从入射到天线阵列上，两个信号的差值从1°～10°变化，信噪比SNR=10 dB。图5为RMSE与信号差值的曲线图。

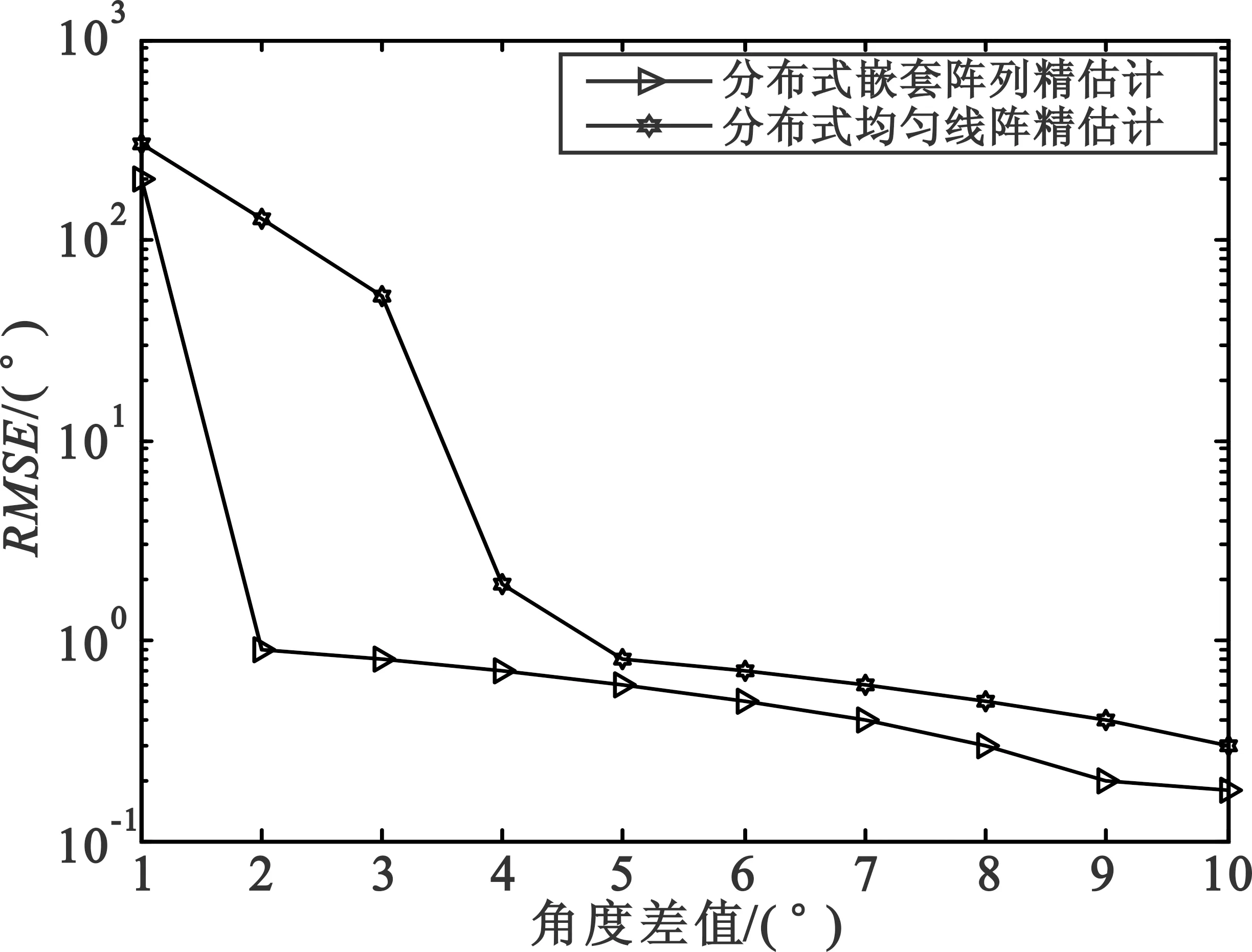
图5 RMSE与角度差值的关系曲线

Fig.5 RMSE curves of DOA estimation versus the angle difference

从图5可以看出，在相同角度差值的情况下，分布式嵌套阵列精估计与分布式均匀线阵精估计相比，明显提高了估计精度。当角度差值仅为3°时，两种阵列结构均能准确估计出信号的来波方向。

仿真4信号与仿真1相同，SNR=10 dB，独立蒙特卡洛试验次数从100～800变化。图6为RMSE与独立蒙特卡洛试验次数的曲线图。

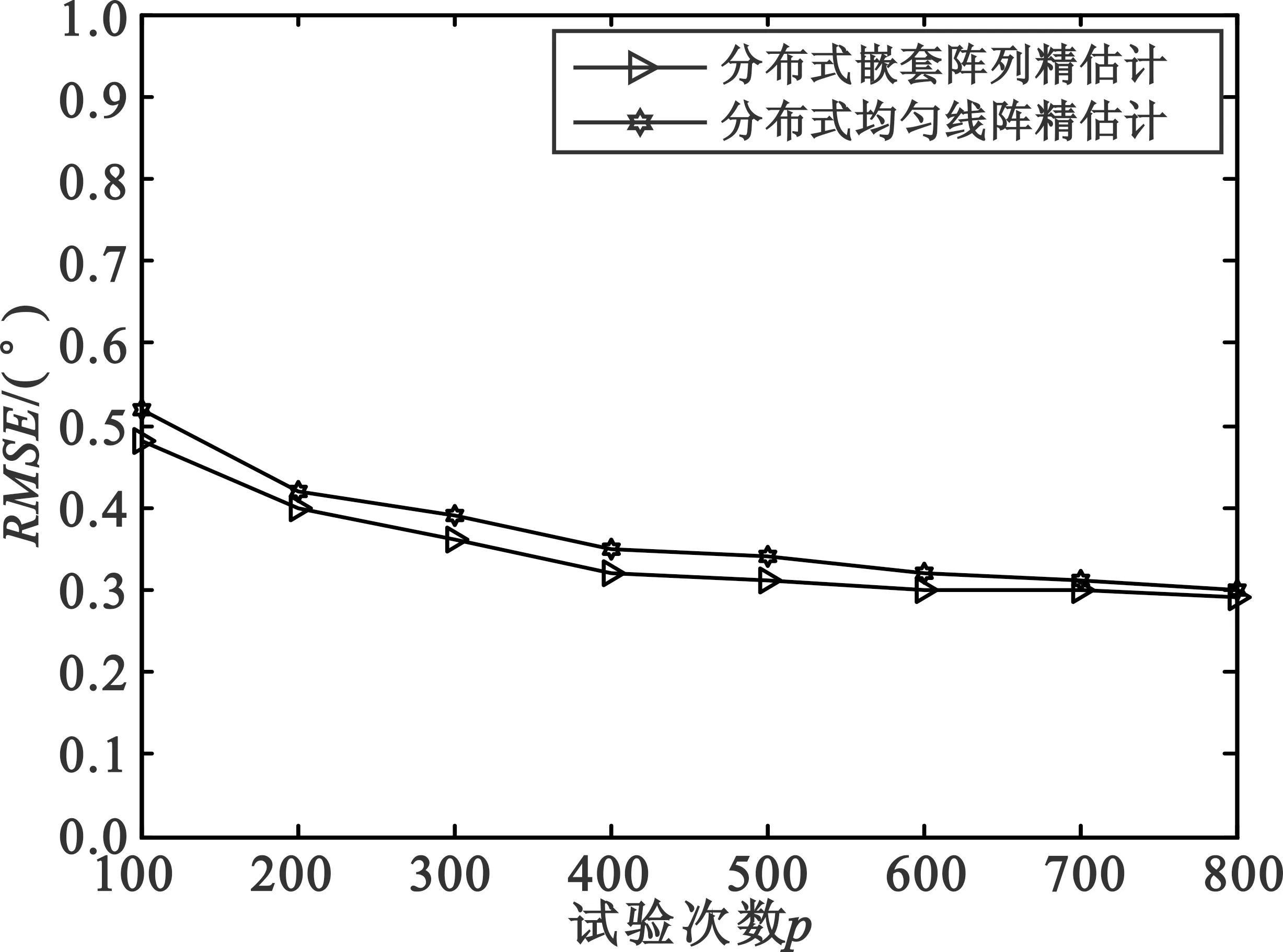
图6 RMSE与独立蒙特卡洛试验次数的关系曲线

Fig.6 RMSE curves of DOA estimation versus the number of Monte-Carlo

从图6可以看出，在相同独立蒙特卡洛试验次数的情况下，分布式嵌套阵列精估计与分布式均匀线阵精估计相比，明显提高了估计精度。这是因为嵌套阵列经过高阶累积量和Khatri-Rao积运算后，可以生成具有更多虚拟阵元的阵列天线结构。

5 结束语

本文提出了一种分布式嵌套阵列天线结构，该阵列天线结构由两个相互独立的四级嵌套子阵构成，而已有的分布式阵列天线结构以相互独立的均匀直线作为子阵。对所提阵列天线接收到的信号进行处理，使用双尺度酉ESPRIT算法得到DOA估计。与分布式均匀直线阵列相比，本文提出的结构可以形成更多的虚拟阵元，增加了最大可估计信号数，提高了估计精度，但与此同时增加了计算量,我们将会在下一步的研究中进行改进。

[1] CHEVALIER P,ALBERA L,FERREOL A，et al.On the virtual array concept for higher order array processing [J].IEEE Transactions on Signal Processing,2005,53(4):1254-1271

[2] CHEVALIER P,FERREOL A,ALBERA L.High-resolution direction finding from higher order statistics:the 2q-MUSIC algorithm [J].IEEE Transactions on Signal Processing,2006,54(8):2986-2997.

[3] MENDEL J M.Tutorial on higher-order statistics(spectra) in signal processing and system theory:theoretical results and some applications [J].IEEE Transactions on Signal Processing,1995,79(3):278-305.

[4] CHEVALIER P,FERREOL A.On the virtual array concept for the four-order direction finding problem [J].IEEE Transactions on Signal Processing,1999,47(9):2592-2595.

[5] SHAMSUNDER S,GIANNAKIS G B.Modeling of non-Gaussian array data using cumulants:DOA estimation of more sources with less sensors [J].IEEE Transactions on Signal Processing,1993,30(3):279-297.

[6] LEMMA A N,VEEN A J,DEPRETTERE E F.Multiresolution ESPRIT algorithm [J].IEEE Transactions on Signal Processing,1993,46(6):1722-1726.

[7] MANIKAS A,PROUKAKIS C.Modeling and estimation of ambiguities in lineat arrays [J].IEEE Transactions on Signal Processing,1998,46(8):2166-2179.

[8] CHEN G H,CHEN B X,YANGM L.High accuracy 2-D angle estimation using distributed coherent arrays [J].Journal of Electronics & Information Technology,2012,34(11):2621-2627.

[9] VASYLYSHYN V I.Unitary ESPRIT-based DOA estimation using sparse linear dual size spatial invariance array [C]//Proceedings of 2014 European Radar Conference.Paris,France:IEEE,2014:1-5.

[10] PAL P,VAIDYANATHAN P P.Nested arrays:a novel approach to array processing with enhanced degrees of freedom [J].IEEE Transactions on Signal Processing,2010,58(8):4167-4181.

[11] PAL P,VAIDYANATHAN P P.Multiple level nested array:an efficient geometry for 2qth order cumulant based array processing [J].IEEE Transactions on Signal Processing,2012,60(3):1253-1269.

[12] PAL P,VAIDYANATHAN P P.Nested arrays in two dimensions Part I:geometrical considerations[J].IEEE Transactions on Signal Processing,2012,60(9):4694-4718.

谢玉凤(1990—)，女，吉林省吉林市人，硕士研究生，主要研究方向为阵列信号处理中的波达方向估计；

XIE Yufeng was born in Jilin,Jilin Province,in 1990.She is now a graduate student.Her research concerns DOA estimation in array signal processing.

Email：superxieyufeng@sina.com

白 媛(1971—)，女，吉林省吉林市人，教授，主要研究方向为阵列信号处理中的波达方向估计；

BAI Yuan was born in Jilin,Jilin Province,in 1971.She is now a professor.Her research concerns DOA estimation in array signal processing.

马秀荣(1961—)，女，河北张家口人，教授，主要研究方向为阵列信号处理中的波达方向估计。

MA Xiurong was born in Zhangjiakou,Hebei Province,in 1961.She is now a professor.Her research concerns DOA estimation in array signal processing.

Distributed Nested Array and Its DOA Estimation

XIE Yufeng1,2,BAI Yuan1,2,MA Xiurong1

(1.School of Computer and Communication Engineering,Tianjin University of Technology,Tianjin 300384,China;2.Guilin University of Electronic Technology,Guilin 541004,China)

A distributed nested array composed of two independent four-level nested sub-arrays is proposed.There exists a baseline between the two sub-arrays,and the baseline meets the corresponding condition.According to the array,three identical uniform linear arrays(ULAs) can be obtained through high order cumulant and Khatri-Rao product operation of the received signals.The unitary estimation of signal parameters via rotation invariance techniques(ESPRIT) based on the spatial smoothing method is applied to the new array to estimate the direction of arrival(DOA).The algorithm can efficiently improve the degree of freedom.The simulation results prove the effectiveness of the proposed algorithm.

distributed nested array;high order cumulant;uniform linear array;direction of arrival estimation

10.3969/j.issn.1001-893x.2016.07.012

谢玉凤，白媛，马秀荣.分布式嵌套阵列及其DOA估计[J].电讯技术，2016,56(7)：783-787.[XIE Yufeng,BAI Yuan,MA Xiurong.Distributed nested array and its DOA estimation[J].Telecommunication Engineering,2016,56(7)：783-787.]

2015-12-16；

2016-04-19 Received date:2015-12-16；Revised date：2016-04-19

天津市科技创新专项基金(10FDZDGX00400)

Foundation Item:Tianjin Science and Technology Innovation Fund(10FDZDGX00400)

TN953.7

A

1001-893X(2016)07-0783-05

**通信作者：superxieyufeng@sina.com Corresponding author：superxieyufeng@sina.com