内置式永磁电机齿槽转矩的解析计算

李桂丹,王佐民,李 斌

(天津大学,天津 300072)



内置式永磁电机齿槽转矩的解析计算

李桂丹,王佐民,李 斌

(天津大学,天津 300072)

利用定子侧边力法分析了内置式永磁电机齿槽转矩。在基于等效磁网络法的基础上求解出内置式永磁电机的气隙磁密，进而将其等效为表贴式结构。在此基础上，建立了等效电机单槽模型，获得了齿槽转矩各阶谐波分量，进而根据槽空间相位关系合成了电机总的齿槽转矩，提高了计算效率。计算结果与有限元法所得出的结果进行了比较，验证了本方法的正确性。

齿槽转矩;内置式永磁电机;单槽模型;侧边力;合成

0 引 言

永磁电机以其高功率密度、高效率等优点，得到了国内外学者的广泛关注。相比表贴式结构，内置式永磁电机永磁磁极埋于转子内部，可以克服高转速下对永磁体的离心力作用；弱磁能力强，能够在较宽的调速范围内运行；磁阻转矩分量增大了电机的输出转矩。基于这些优势，内置式永磁电机在驱动设备中，特别是新能源电动汽车中应用广泛。

永磁电机定子齿壁与永磁体间存在齿槽转矩，齿槽转矩会在电机运动时导致转矩波动，从而产生噪声、振动。针对表贴式永磁电机，国内外学者利用能量法，侧边力法等[1-3]分析了电机齿槽转矩。研究表明能量法模型受槽漏磁和永磁体间漏磁影响较大，侧边力法可以更准确的求解出齿槽转矩[4]。相比表贴式结构，内置式永磁电机有效气隙小，齿槽转矩的影响更大[5]。文献[6-8]采用有限元法分别研究了永磁体不对称、定子铁心形状、永磁体分段对内置式永磁电机齿槽转矩的影响。但有限元法耗时较长，尤其在电机优化设计阶段，这个问题更为突出。解析法以数学模型的形式直观体现电机参数与齿槽转矩的联系，具有更明确地物理意义，并且可以与多种优化算法结合达到优化电机参数的目的。文献[9]在能量法基础上，推导了齿槽转矩解析模型，结合梯度下降法对内置式永磁电机参数进行优化，削弱了齿槽转矩；文献[10]采用能量法和傅里叶分解法结合研究了槽口宽度对内置式永磁电机齿槽转矩的影响；文献[11]利用等效虚拟磁极，将侧边力法应用于多层U型内置式永磁电机齿槽转矩解析计算，但在齿槽转矩求解时，每一个步长需要累加全部齿产生的齿槽转矩，计算量较大。

本文对一型内置式永磁电机齿槽转矩的解析计算进行了研究，在忽略齿槽效应的情况下采用等效磁路法求解了电机径向磁密，建立了等效电机单槽模型，利用侧边力法对单槽内置式永磁电机齿槽转矩进行求解，获得了各阶谐波分量，进而根据槽空间相位关系合成了电机总的齿槽转矩，给出了各阶谐波变化规律，提高了计算效率。通过有限元仿真验证了该方法的正确性。

1 内置式永磁电机齿槽转矩摸型

本模型选取了单层“一”型永磁体结构的内置式永磁电机作为研究对象。图1中分别为一台4极6槽和4极12槽的内置式永磁电机，表1给出了电机的参数。

图1 内置式永磁电机模型

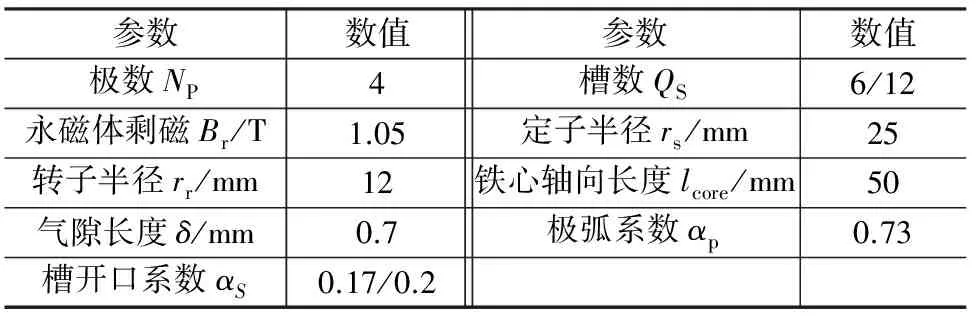
参数数值参数数值极数NP4槽数QS6/12永磁体剩磁Br/T1．05定子半径rs/mm25转子半径rr/mm12铁心轴向长度lcore/mm50气隙长度δ/mm0．7极弧系数αp0．73槽开口系数αS0．17/0．2

图2是用有限元软件仿真得到的磁场分布图。在电机设计的初级阶段，为了解析计算的快速与简捷性，假设电机定子是连续平滑的，即忽略电机定子的齿槽效应。

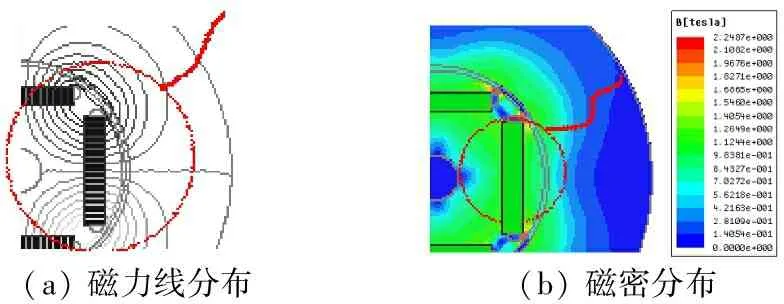
(a)磁力线分布(b)磁密分布

图2 1/4内置式永磁电机的磁场分布

图2(a)给出了电机磁力线分布，图2(b)为电机磁密分布图。可以看出，一个磁极的一半磁力线与另一半相邻磁极形成闭合磁路，永磁体顶端接近转子边缘桥处，出现了明显的磁路饱和问题，在电机其他部位饱和不显著。因此在计算气隙磁密时，需要计及转子边缘桥部位饱和的影响。

图3是1/4电机集中参数等效磁路图。图中，φg是一个磁极下内置式永磁体单独激励时的气隙磁通，φr是一个磁极激励产生的磁通；Rg，Rmo分别是一个磁极下气隙磁阻、永磁体磁阻；Rml，Rmb分别是永磁体端部漏磁磁阻、转子边缘桥漏磁磁阻；Rr，Rs分别是转子轭磁阻，定子轭磁阻。转子轭与定子轭在一般情况下不会出现饱和，所以Rr，Rs与Rg相比较的话可以忽略不计。

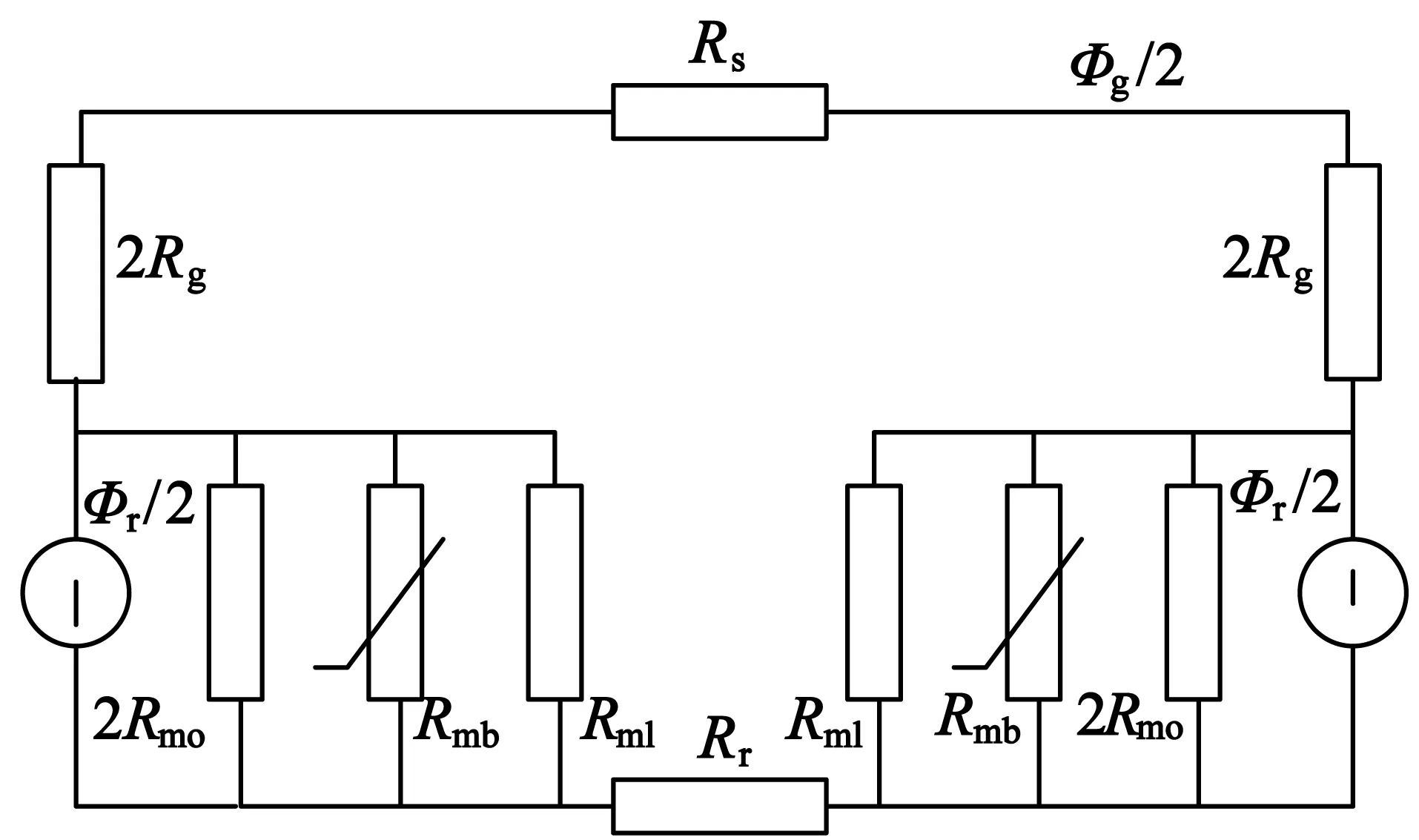
图3 集中参数等效磁路

由于转子边缘桥出现磁路饱和问题，Rmb不是线性，可表示:

(1)

其中：Amb=lb，l为铁心长度，b为边缘桥宽度。

通过该磁阻的漏磁磁通:

(2)

为避免迭代运算，根据该定子铁心材料的B-H曲线，可直接给定饱和工作点的磁通密度[12]。本文选取Bmb=1.7T，进而由图3可以得到气隙磁通量φg，进而得到气隙磁密Bg。

另外，从图2(a)中还可看出，内置式永磁电机的气隙磁密接近于径向，此时可以将其等效为一个虚拟永磁体厚度为0，相对磁导率为1的表贴式永磁电机[11]。因此，可直接应用表贴式永磁电机齿槽转矩的解析算法来进行求解。

选取计算侧边力方法，图4给出了理想气隙磁力线分布，其中，hm为等效永磁体的厚度；μr为永磁体的相对磁导率。为了简化齿槽转矩的计算，作如下假设[1]:槽型简化为矩形；磁场分布由永磁体和相对磁导率乘积决定的；磁力线在气隙处为直线，在槽中面对齿壁处的磁力线路径是四分之一圆;定子铁心相对磁导率无穷大。

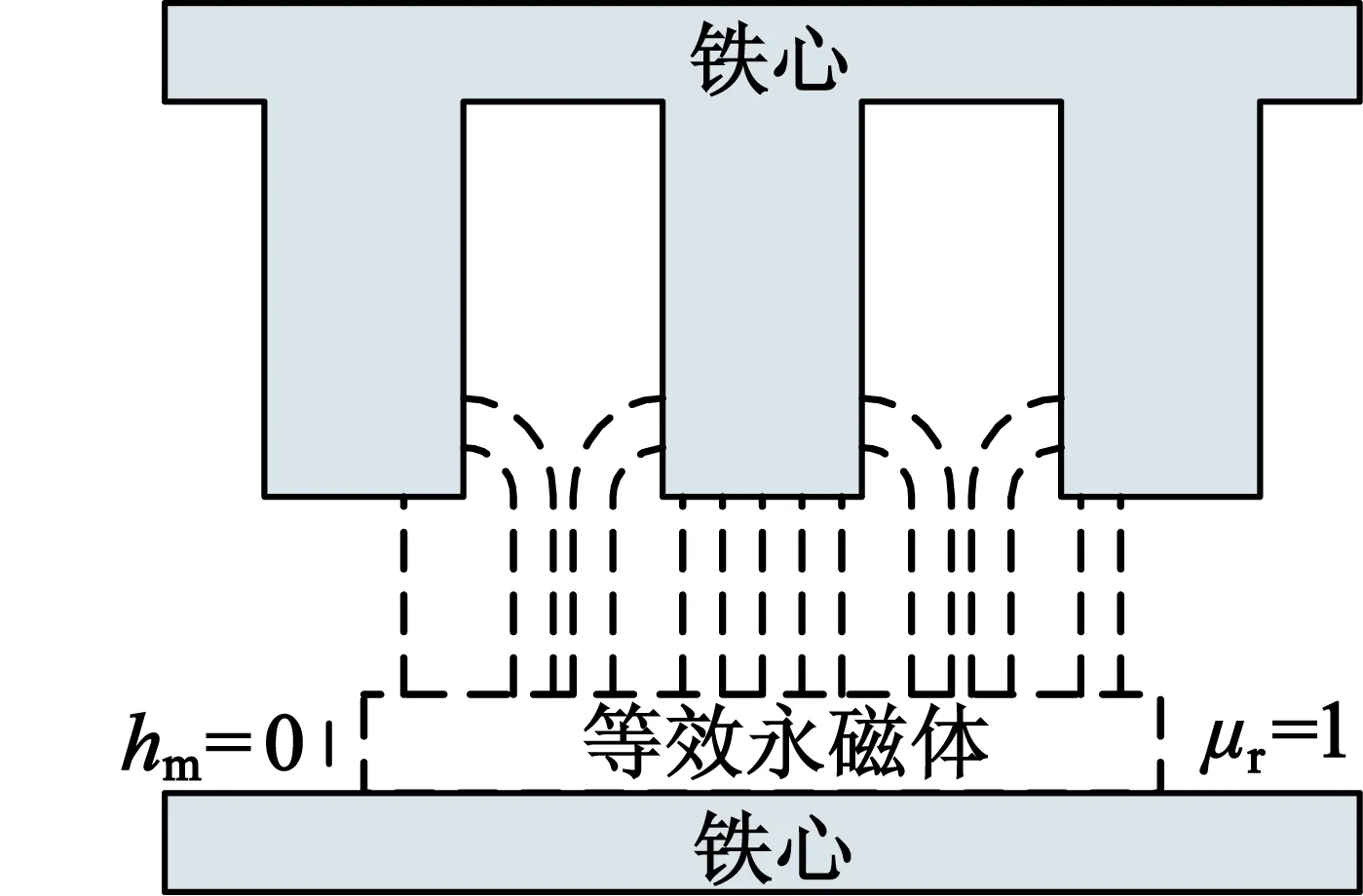
图4 理想化的磁力线分布图

侧边力作用在定子齿上，进而产生齿槽转矩。假设定子齿壁处磁密等于槽开口处磁密，那么，内置式永磁电机的齿槽转矩就可以通过下式计算[1]：

(3)

(4)

(5)

(6)

式中：Br1，Br2分别为磁力线垂直于齿壁处的磁密值；λ，λr分别为磁导率与相对磁导率。其他参数如图5所示。

图5 侧边力

2 齿槽转矩的合成

在直接计算内置式永磁电机齿槽转矩时，在每一个分析步长，需要将全部齿槽产生的齿槽转矩叠加，从而得到总的电机齿槽转矩。为提高分析效率，建立单槽电机模型，如图6所示，分别为4极6槽与4极12槽的单槽内置式永磁电机，其中电机齿槽尺寸与图1中电机一致。

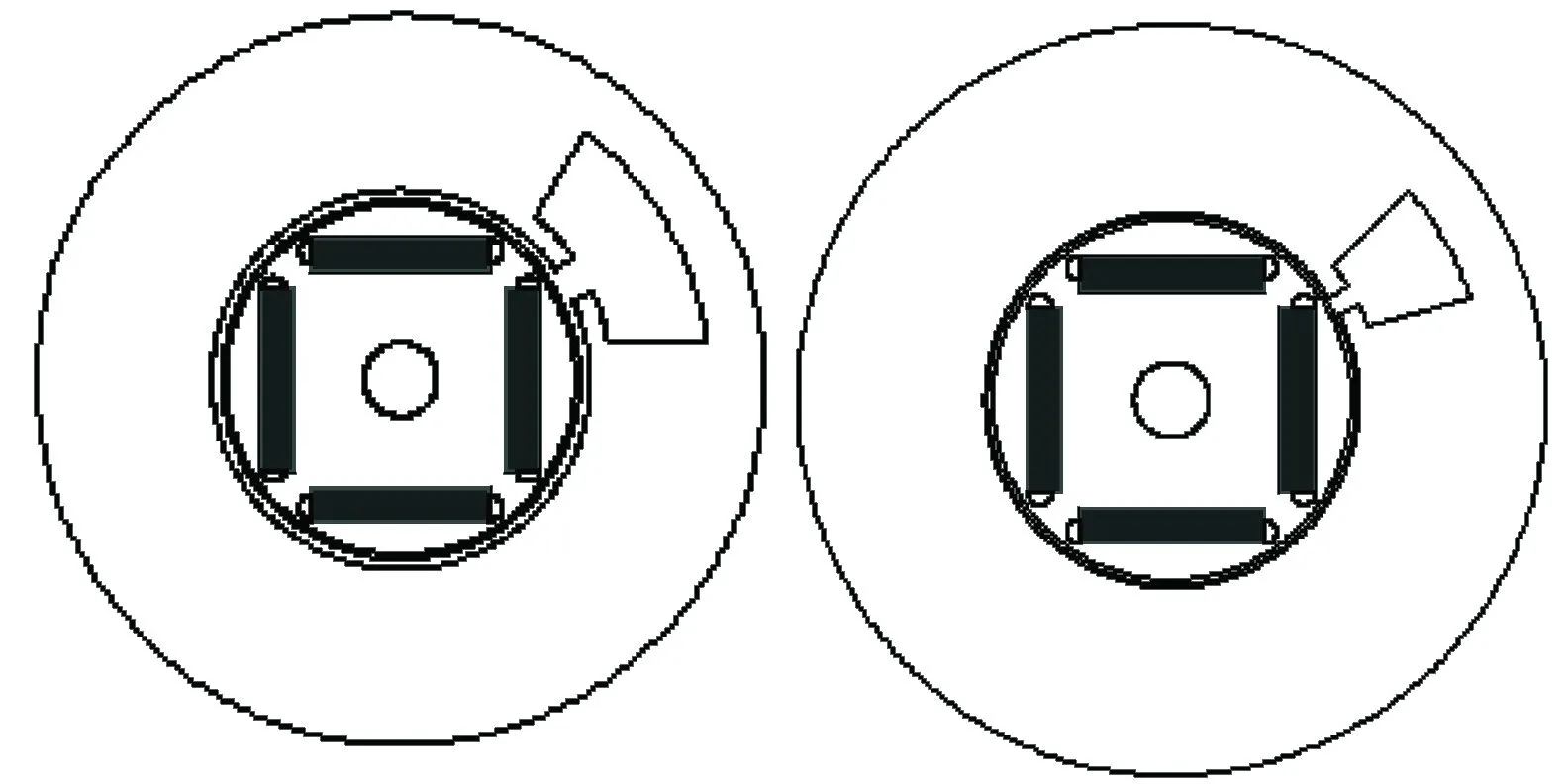
图6 单槽电机模型

以图6为基础，利用式(3)计算出单槽电机的齿槽转矩Tsc(α)，可以表示为傅里叶级数：

(7)

式中:Tscn为Tsc的n次谐波的幅值。根据叠加原理[13]将单槽齿槽转矩合成为由全部齿槽产生的电机的整体齿槽转矩，傅里叶级数表示：

(8)

根据式(8)，分别给出4极6槽与4极12槽内置式永磁电机的全槽齿槽转矩:

(9)

(10)

由式(7)、式(9)、式(10)可以得到，单槽电机的各次谐波不是全部参与全槽电机的齿槽转矩合成，只有3n次谐波，这是由全槽电机的槽极数决定的。

3 齿槽转矩解析结果与有限元仿真

图7、图8分别为4极6槽与4极12槽内置式永磁电机的径向气隙磁密。

图7中，在忽略齿槽时，通过等效磁路法与有限元法求得的气隙磁密误差小于4%，求解结果较为准确；但由于实际电机模型中存在的齿槽效应，4极6槽电机气隙磁密在经过齿槽时小于忽略齿槽时的计算数值，也就导致了解析法齿槽转矩在齿槽开口处要大于有限元仿真结果，如图9所示。图8中考虑齿槽与忽略齿槽时的有限元求解的气隙磁密对比发现，虽然在经过齿槽时磁密值出现波动，但两者气隙磁密均值误差小于3.7%，电机齿槽转矩解析法与有限元所得结果吻合度较高。

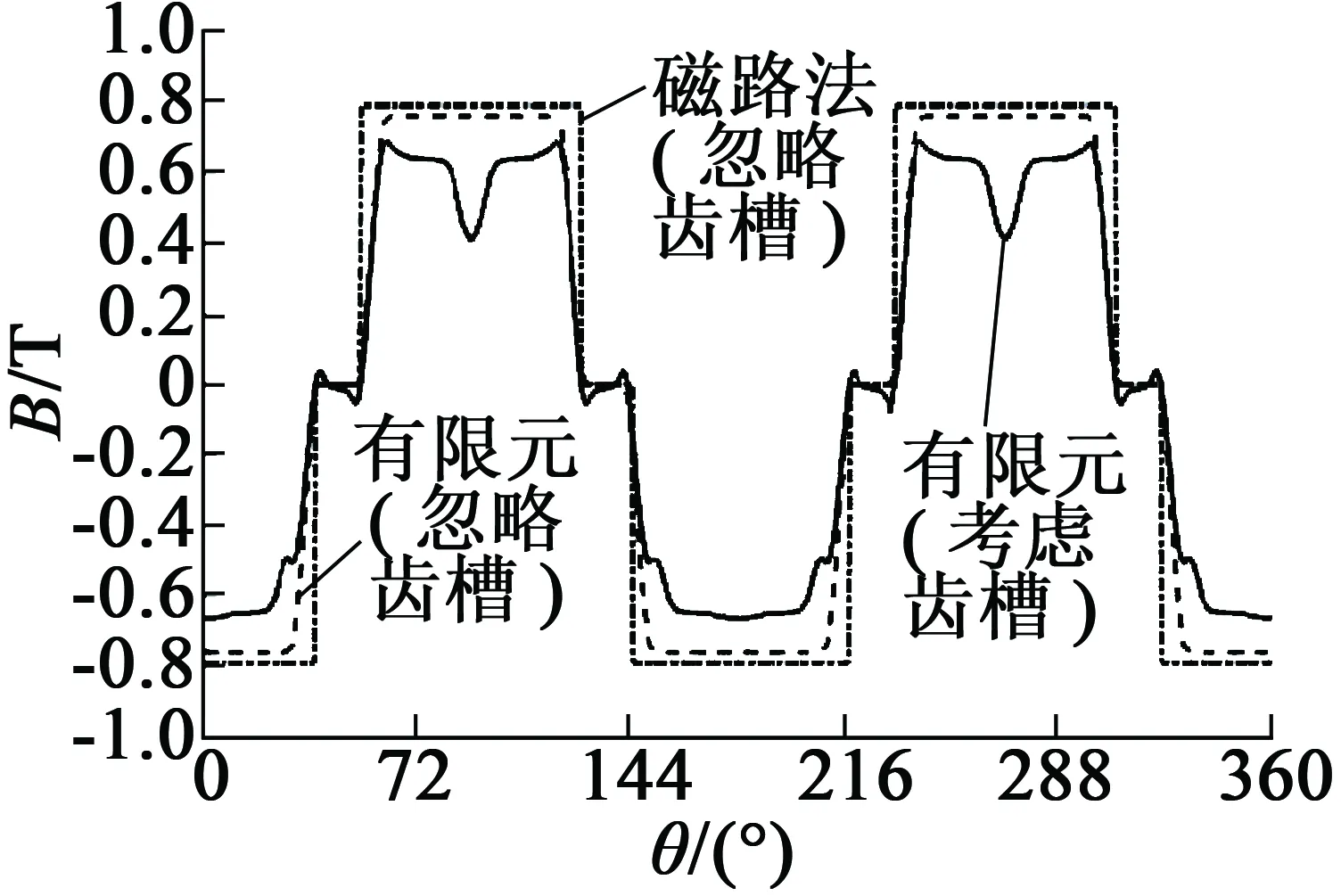
图7 4极6槽内置式永磁电机径向气隙磁密

图8 4极6槽内置式永磁电机径向气隙磁密

图9、图10分别为为4极6槽、4极12槽电机齿槽转矩。

图9 4极6槽永磁电机齿槽转矩

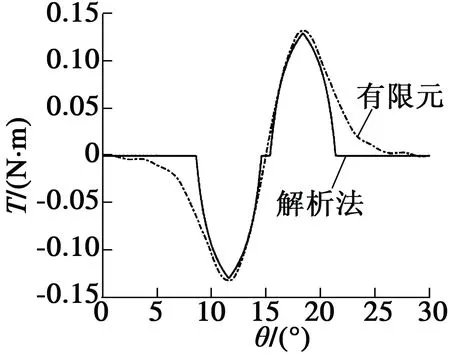
图10 4极12槽永磁电机齿槽转矩

可以看出，图9、图10中解析算法求得的齿槽转矩与有限元法在求解结果基本吻合。存在的误差主要是由在近似计算时假设定子铁心无穷大导致的。同时，在计算齿槽转矩时，对磁力线分布进行了理想化假设，而实际情况中，气隙磁密不完全是沿径向分布的，这也是导致计算误差的原因之一。

图11、图12图分别为6槽、12槽的单槽电机齿槽转矩。得到单槽电机齿槽转矩后，可以根据式(9)、式(10)合成全槽电机齿槽转矩，这与式(3)所得到的解析结果一致，但计算效率提高。

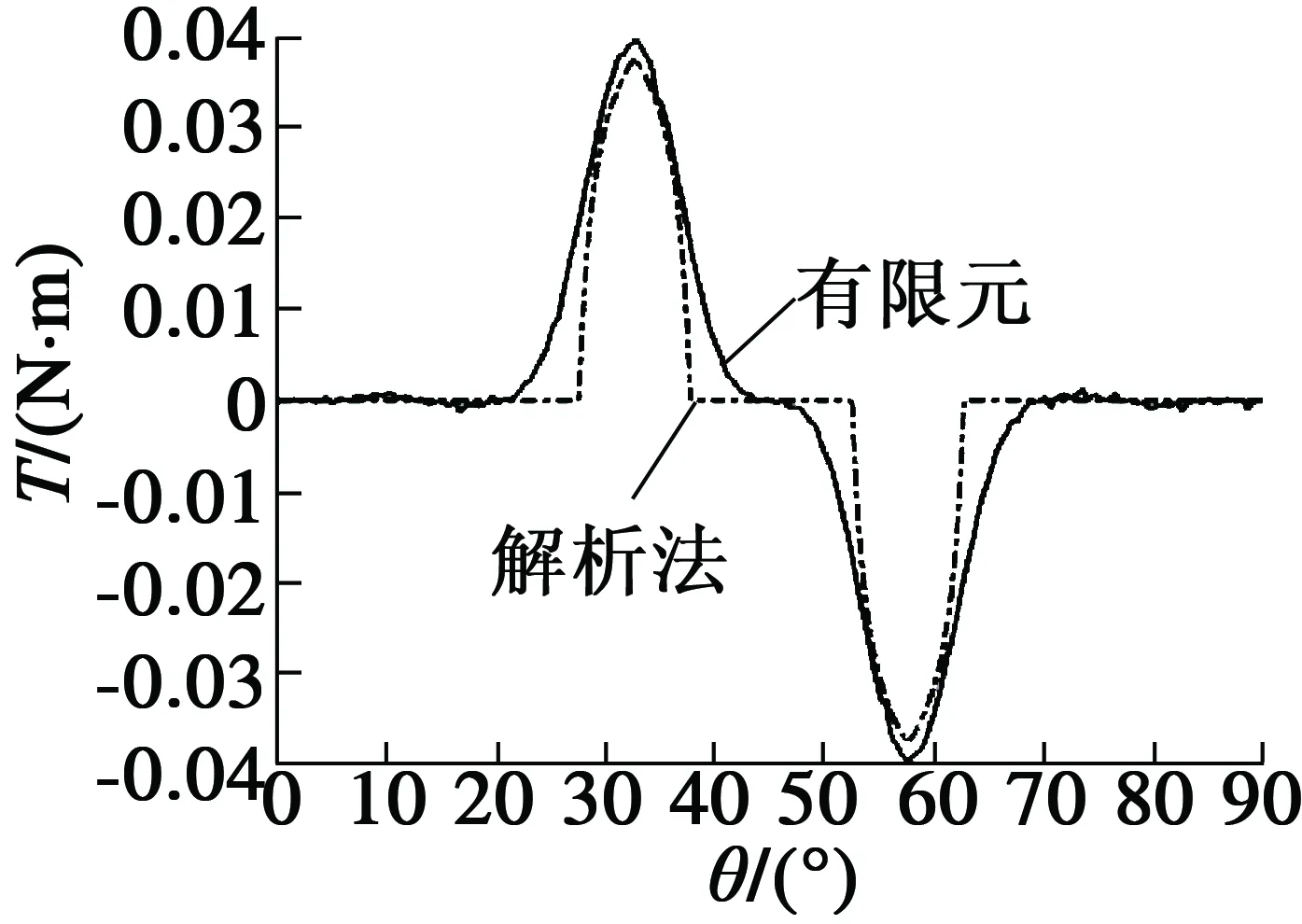
图11 6槽单槽电机齿槽转矩

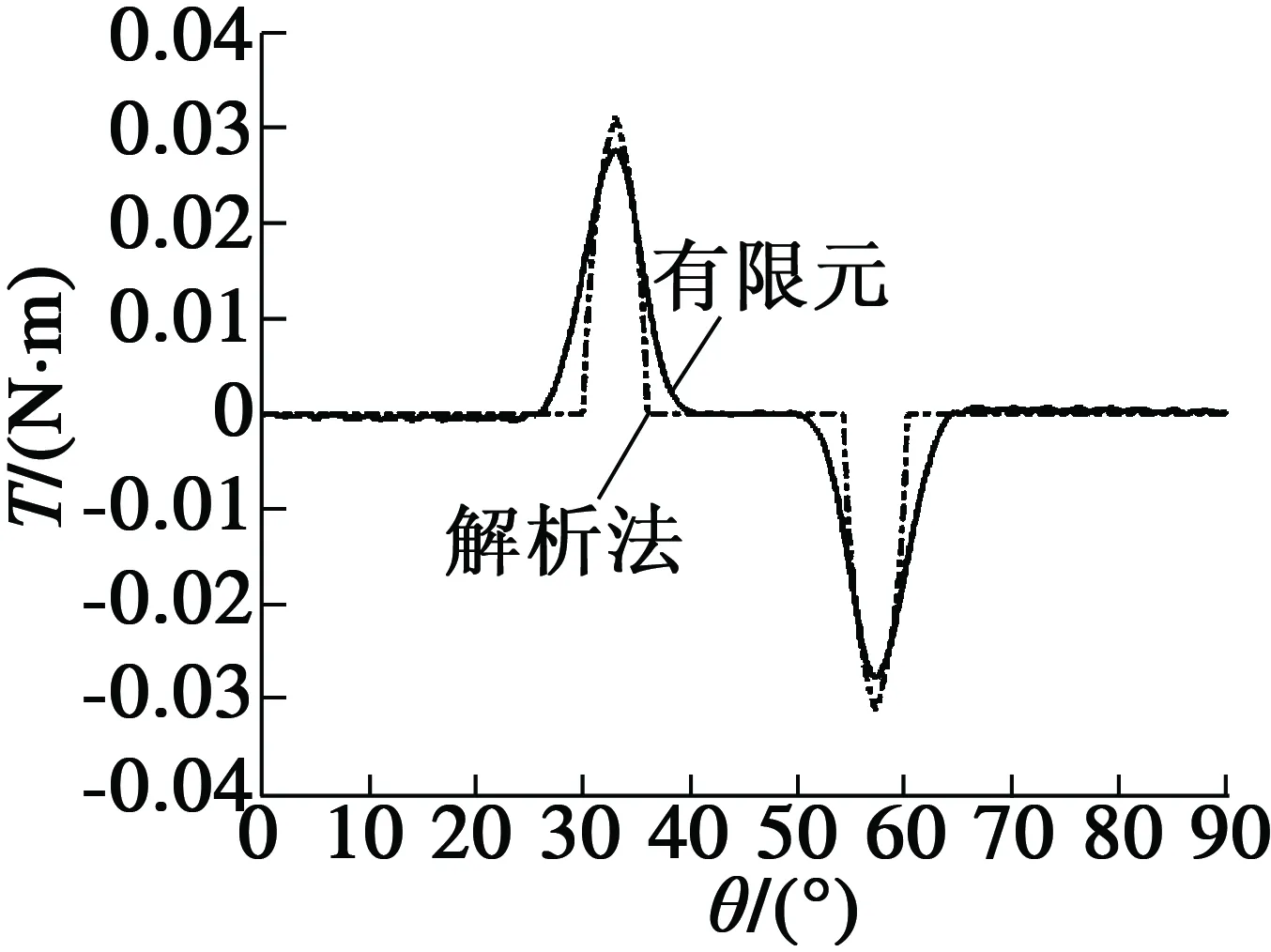
图12 12槽单槽电机齿槽转矩

为了对比单槽与多槽电机齿槽转矩间的联系，分别对6槽电机与12槽电机的单槽与全槽电机齿槽转矩进行了傅里叶分解。对比图13与图14的各次谐波可以得出，当由单槽电机的齿槽转矩解析合成全槽电机的齿槽转矩时，单槽电机齿槽转矩的各次谐波不会全部参与多槽电机的齿槽转矩合成；由于4极6槽与4极12槽电机的槽极数的最小公倍数都为24，所以全槽转矩谐波中只有单槽电机转矩的3^n次谐波。内置式永磁电机的槽极数共同决定了齿槽转矩解析合成算式各项系数，即算式中出现的各次谐波的幅值大小与各次谐波次数。

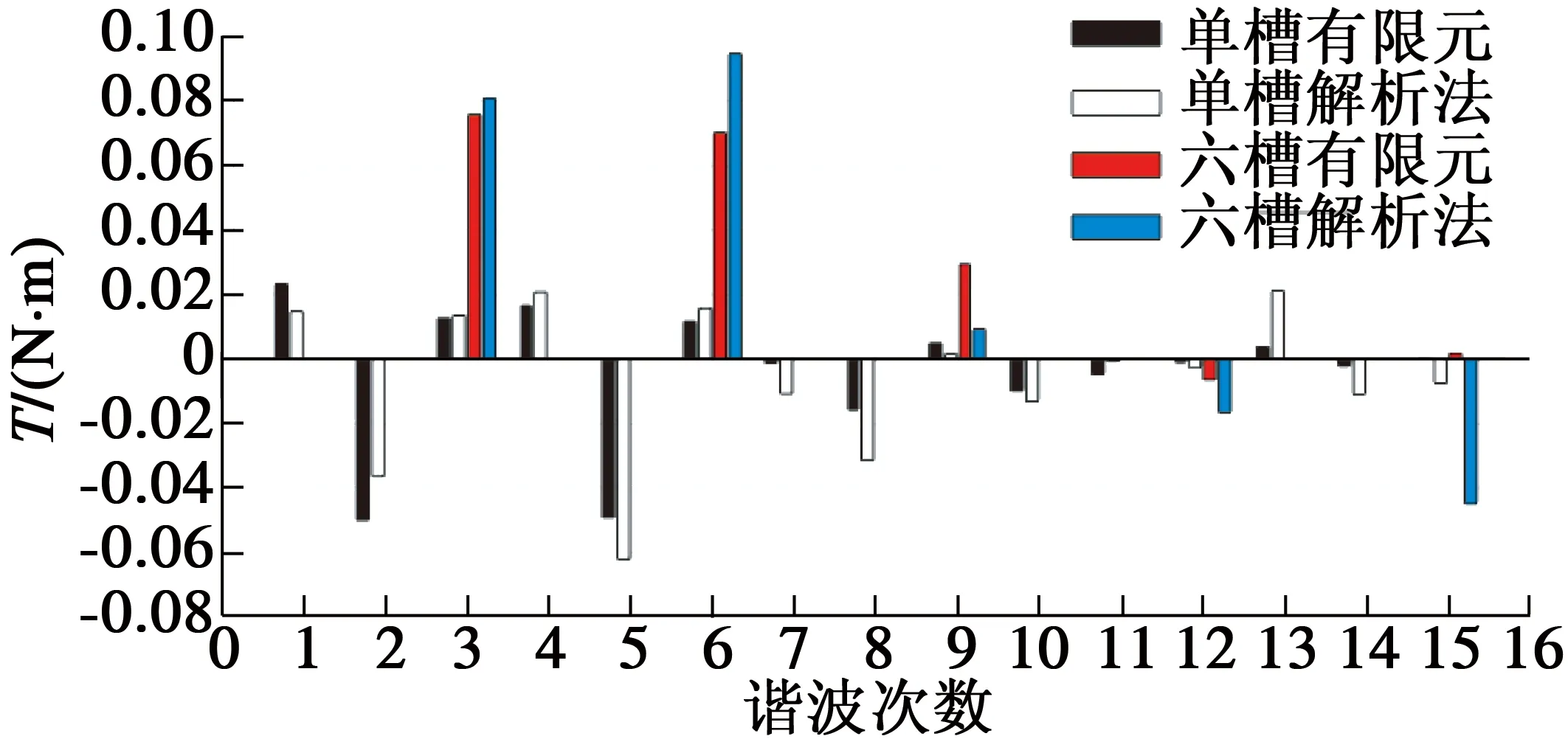
图13 6槽电机单槽与六槽齿槽转矩谐波次数

图14 12槽电机单槽与十二槽齿槽转矩谐波次数

其中，4极6槽内置式永磁电机齿槽转矩的各次谐波幅值为其单槽电机的3n次谐波的6倍；4极12槽内置式永磁电机齿槽转矩的各次谐波幅值为其单槽电机的3n次谐波的12倍；并且由各次谐波变化趋势可以看出，有限元仿真所得结果与解析法所得结果变化趋势一致，验证了解析法的正确性。

图15、图16为选取电机不同槽开口系数时的齿槽转矩峰值。

图15 4极6槽齿槽转矩峰值

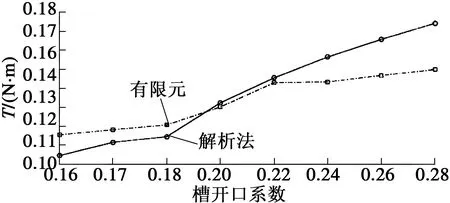
图16 4极12槽齿槽转矩峰值

通过有限元与解析法的对比发现，当槽开口系数大于0.22时，两者的计算误差明显增大；当槽开口系数小于0.22时，解析法计算结果与有限元更接近，这与表贴式电机分析结论一致[4]。目前工业用电机为了避免齿槽效应，多选用半闭口槽，即槽开口系数要小于0.22。所以，该解析算法适用于求解电机的齿槽转矩。

4 结 语

采用了一种以计算定子侧边力为基础的内置式永磁电机齿槽转矩的解析算法，采用等效磁路法与等效变换计算得到的齿槽转矩具有较高的准确性。同时，解析法求得单槽电机齿槽转矩时，可以用合成法合成相应多槽电机的齿槽转矩，提高计算效率；单槽电机齿槽转矩的各次谐波不会全部参与多槽电机的齿槽转矩合成；全槽内置式永磁电机的槽极数共同决定了齿槽转矩解析合成算式各项系数，即算式中出现的各次谐波的幅值大小与各次谐波次数。在此基础上，讨论了槽开口系数对齿槽转矩的影响。通过有限元仿真验证了该解析法的正确性。

[1]ZHUZQ,HOWED.Analyticalpredictionofthecoggingtorqueinradial-fieldpermanentmagnetbrushlessmotors[J].IEEETransactionsonMagnetics,1992,28(2):1371-1374.

[2] PROCA A B,KEYHANI A,EL-ANTABLY A,et al.Analytical model for permanent magnet motors with surface mounted magnets[J].IEEE Transactions on Energy Conversion,2003,18(3): 386-391.

[3] 杨玉波,王秀和,丁婷婷,等.极弧系数组合优化的永磁电机齿槽转矩削弱方法[J].中国电机工程学报,2007,27(6):7-11.

[4] 朱莉,姜淑忠,诸自强,等.表面式永磁电机齿槽转矩解析模型比较[J].微电机,2010,43(1):10-15.

[5] KO H-S,KIM K-J.Characterization of noise and vibration sources in interior permanent-magnet brushless DC motors[J].IEEE Transactions on Magnetics,2004,40(6):3482-3489.

[6] 杨玉波,王秀和.永磁体不对称放置削弱内置式永磁同步电动机齿槽转矩[J]. 电机与控制学报,2010,14(12):58-62.

[7] KIM D H,PARK I H,LEE J H,et al.Optimal shape design of iron core to reduce cogging torque of IPM motor[J].IEEE Transactions on Magnetics,2003,39(3):1456-1459.

[8] 谢芳,黄守道,刘婷.内置式永磁电机齿槽转矩的分析研究[J].微特电机,2009,37(11):11-14.

[9] WANG Daohan,WANG Xiuhe,KIM M-K,et al.Integrated optimization of two design techniques for cogging torque reduction combined with analytical method by a simple gradient descent method[J]. IEEE Transactions on Magnetics,2012.48(8): 2265-2276.

[10] 杨玉波,王秀和,朱常青.电枢槽口宽度对内置式永磁同步电机齿槽转矩的影响[J].电机与控制学报,2011,15(7):21-25.

[11] SEO J H,CHOI H S.Analytical modeling for calculating cogging torque in interior permanent magnet machine with multi flux-barriers[J].IEEE Transactions on Applied Superconductivity,2004,24(3):1-4.

[12] ZHU L,JIANG S Z,ZHU Z Q，et al.Analytical modeling of open-circuit air-gap field distributions in multisegment and multilayer interior permanent-magnet machines[J].IEEE Transactions on Magnetics,2009,45(8):3121-3130.

[13] ZHU Z Q,RUANGSINCHAIWANICH S,HOWE D.Synthesis of cogging-torque waveform from analysis of a single stator slot[J].IEEE Transactions on Industry Applications,2006,42(3): 650-657.

Analytical Calculation of Cogging Torque for Interior Permanent Magnet Machine

LI Gui-dan,WANG Zuo-min,LI Bin

(Tianjin University,Tianjin 300072,China)

The cogging torque of interior permanent magnet machine (IPM) is analyzed using the lateral force method. The magnet flux density of air gap is calculated based on the equivalent magnet circuit (MEC), then the IPM can be transformed into an equivalent surface permanent magnet machine (SPM) model. To improve the computational efficiency, a single slot machine model is built. Based on this, the cogging torque is calculated and the harmonic components are obtained. According to space phase relationship of stator slots, the total cogging torque of the equivalent SPM, i.e. the original IPM, can be synthesized. Finally, the finite element analysis is used to validate the proposed method.

cogging torque; interior permanent magnet machine (IPM); single slot model; lateral force; synthesis

2016-03-28

TM351

A

1004-7018(2016)10-0026-04

李桂丹(1975-)，女，副教授，研究方向为电机设计及控制。