二维DGTD方法中UPML吸收边界的实现

李林茜，魏 兵，杨 谦，葛德彪

(1. 西安电子科技大学 物理与光电工程学院，陕西 西安 710071; 2. 西安电子科技大学 信息感知协同创新中心，陕西 西安 710071)



二维DGTD方法中UPML吸收边界的实现

李林茜1,2，魏 兵1,2，杨 谦1,2，葛德彪1,2

(1. 西安电子科技大学 物理与光电工程学院，陕西 西安 710071; 2. 西安电子科技大学 信息感知协同创新中心，陕西 西安 710071)

针对二维情形单轴各向异性完全匹配层吸收边界条件，研究了横磁波情形时域离散伽略金算法单轴各向异性完全匹配层吸收边界的理论基础和实现方案．借鉴时域有限差分方法——时域离散伽略金算法中吸收边界阻抗匹配、各向异性介质参数设置和匹配矩阵等思想，结合时域离散伽略金算法空间离散网格的非结构特性和离散单元之间场量传递的特点，给出了在单轴各向异性完全匹配层中电磁场量时域迭代公式，进一步离散成为离散时域迭代计算式．由于时域离散伽略金算法网格的非结构特性，一阶SM吸收边界条件一般对入射电磁波的反射率在 -24 dB 左右．仿真算例说明，给出的时域离散伽略金算法单轴各向异性完全匹配层吸收边界对电磁波的双重衰减达 130 dB，表明单轴各向异性完全匹配层具有良好的吸收效果．关键词：时域离散伽略金方法;单轴各向异性完全匹配层;横磁波

截断边界条件是许多电磁场数值方法精度保证的关键．在过去几十年，学着们提出许多种吸收边界条件，并成功应用于时域有限差分(Finite Difference Time Domain， FDTD)等方法中[1-2]．文献[3]中提出了完全匹配层(Perfectly Matched Layer， PML)吸收边界，该边界是在计算域最外面增加一层非物理吸收层，该吸收层与相邻区域阻抗匹配，进入PML层的电磁波因为层内介质参数渐变而迅速衰减．后来有人提出的坐标伸缩完全匹配层(Coordinate stretched Perfectly Matched Layer， CPML)以及各向异性完全匹配层(Uniaxial anisotropy Perfectly Matched Layer， UPML)，均具有良好效果．

时域离散伽略金(Discontinuous Galerkin Time Domain， DGTD)方法[4-5]是基于时域体积元发展起来的一种兼备时域有限元(Finite Element Time Domian，FETD)方法网格剖分的灵活性和FDTD显式迭代特点的算法．文献[6]中将PML技术应用于DGTD，其后，文献[7]将PML技术应用于共形的三维DGTD计算．文献[8]提出一种DGTD提高PML稳定性的方案．文献[9-10]中讨论了高阶结点DGTD方法中的PML问题．上述文献主要讨论三维问题，然而在很多的情形，例如金属搭接缝中的电波传播问题、层状介质中的波传播问题、地面上方长传输线的电磁场分布、地下长线缆的电磁场分布问题和光纤里的光传输问题等都可以简化成二维问题来处理．考虑到二维方案在解决许多问题中方便快捷的特性，系统地研究DGTD算法的二维UPML吸收边界具有重要的意义．

文中从各向异性介质中的Maxwell方程组和UPML基本理论出发，得到UPML介质层中的支配方程和辅助方程．考虑到DGTD空间离散网格的非结构特性，结合离散单元之间场量传递的特点，将方程加权积分得到单元矩阵方程．进一步，考虑相邻单元之间电磁场矢量切向分量突变的通量边界条件，通过基函数展开和矩阵单元计算，得到具有通量形式的时域公式，进而得到横磁(Transverse Magnetic，TM)波情形UPML中的时域迭代计算式．数值结果说明，文中UPML吸收边界对电磁波的衰减达 130 dB，吸收效果良好，满足二维情形电磁场精确仿真的需求．

1 二维UPML基本理论

UPML是指在计算域外部增加一层非物理区域，该区域中为各向异性介质．实际操作中适当选择各向异性介质的本构参数，PML层波阻抗与相邻区域匹配，使入射到分界面上的电磁波无反射地进入该区域．在PML层中，电场和磁场满足的含辅助变量的支配方程为[11]

其中，μ1和ε1为主要计算域中的介电系数和磁导率；a、b和c均为对角张量(具体表示为 a= diag(axx，ayy，azz)，其余类似)；辅助变量Ph和Pe与电场E和磁场H之间满足的微分方程为

其中，d和κ同样为对角阵．UPML实现过程中，需要获得式(1)和式(2)的分量式并离散．

对于TM波，关注的电磁场分量为Ez、Hx和Hy．因此，式(1)可转化为

其中，辅助函数Ph和Pe的分量式为

将式(4)代入式(3)，得TM波情形支配方程式(1)所满足的分量方程，即

方程式(2)的分量式为

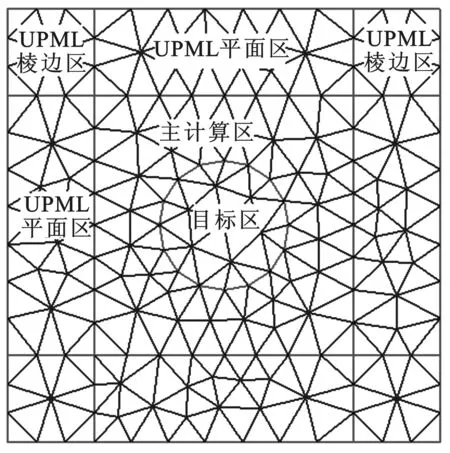
图1 UPML区划分示意图

分量方程式(5)和式(6)在具体实现数值计算时，需要改写为离散的时域递推公式．离散方案依赖于空间离散单元和基函数的选取等．在FDTD方法中常采用六面体离散计算域，并采用点匹配法，而DGTD与FETD类似常采用三维四面体或二维三角形离散单元和伽辽金法．由于采用非结构性网格离散，DGTD的UPML实现更为复杂．

2 二维情形UPML离散DGTD公式

UPML区域划分如图1所示．在包含目标的计算域外部，吸收边界被划分成为4个棱边区和4个平面区．

不同于FETD中单元交界面处采用电磁场连续的强制边界条件，DGTD采用数值通量的方式实现网格之间的场量交互．TM波情形在边界上交互时数值通量定义为[5]

在式(7)通量定义的基础上，通过加权积分[12]和基函数展开，可得分量方程式(5)对应的矩阵方程，即

其中，上标m为单元编号; Mm为单元质量矩阵；Sx和Sy为刚性矩阵；Fe，z、Fh，x和Fh，y分别指电场e和磁场h的通量变化量函数．

将式(8)和式(9)在t=nΔt处离散，式(10)在t=(n+1/2) Δt处离散，可得

其中，αgx、βgx、αgy、βgy、αgz和βgz为常系数．

辅助方程式(6)无需加权积分，直接离散可得

其中，ch、ci、cj和ck为常系数．

式(11)～(16)就是二维TM波情形DGTD算法中UPML区域的递推计算公式．

3 数值算例

设二维计算域为8 m×8 m的矩形，区域离散为 10 902 个结点，共 21 474 个三角形单元，UPML层厚为 1 m．线源在计算域中心处．

UPML层中电导率σ为非均匀分布，其渐变公式为

σ=σmaxd-d0(Δd)mm,

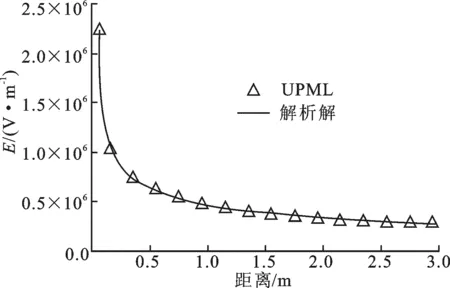
图2 线电流源在自由空间中的辐射电场

其中，d为UPML区中单元的重心坐标位置；d0为UPML内侧界面位置；Δd为UPML层厚度；m为整数，本算例中 m=4．

计算时，时间离散间隔Δt=0.16×10-10s，当辐射电磁波的频率 f=0.3 GHz 时，文中方法的计算结果与利用Hankel函数得到的解析解的比较如图2所示．图2中三角形和实线分别表示文中算法和解析解的结果，由图可见，两种算法的计算结果一致，这说明了文中吸收边界算法的有效性．

为更好地说明电磁波进入UPML层内的衰减情况，下面给出在辐射线源和计算域最外端连线上场值的分布情形．图3(a)是线元辐射的场值快照，线源位于A点处．线段AB上的电场如图3(b)所示，由图可见，电磁波在刚进入UPML层的阶段衰减不大(这是由于界面附近参数接近于内部计算域，便于电磁波无反射地进入吸收层)．随着电磁波深入UPML层，衰减量逐步加大(吸收层参数设置渐变所致)．吸收层界面上场值约为 -25 dB，而到吸收层外侧已下降到 -90 dB 以下．场值衰减为入射场的 1/500，考虑到返回计算域的电场值还需经过相同的路径，这一衰减的效果将加倍．

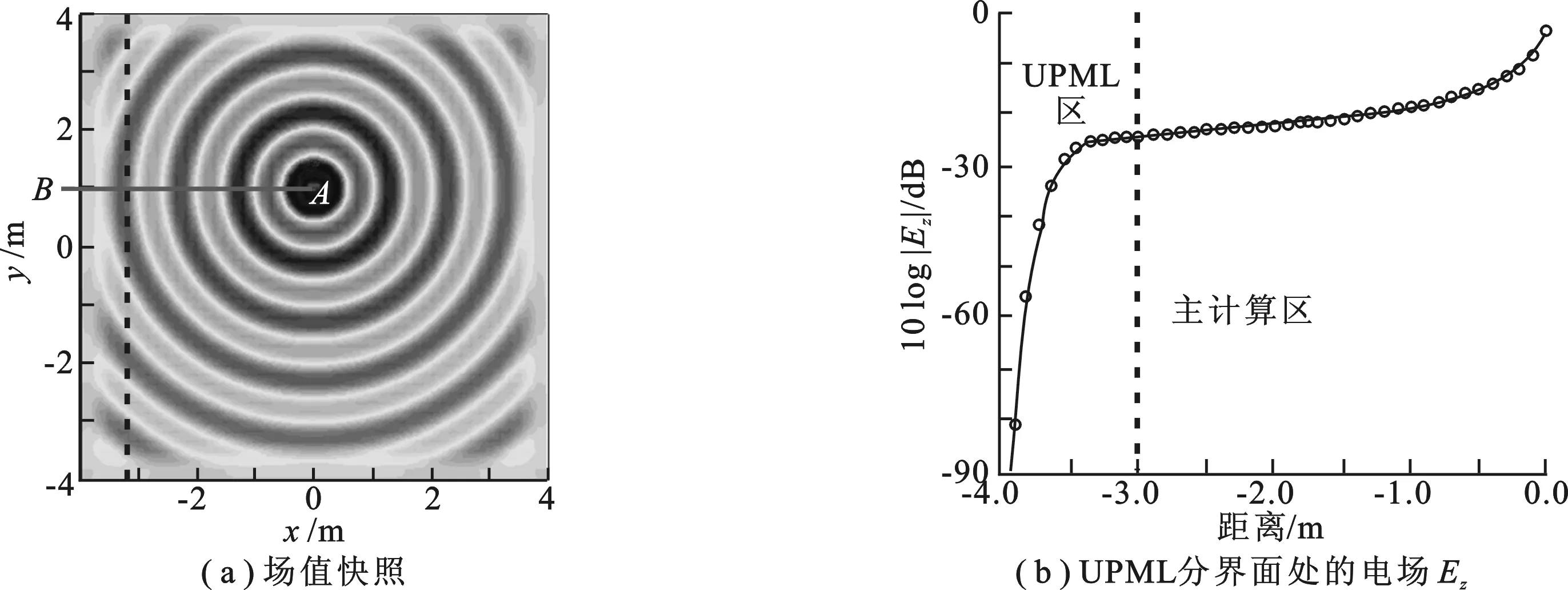
图3 线段AB处的电场Ez

4 结 束 语

文中从二维UPML的基本理论出发，根据空间离散网格的非结构特性，结合DGTD中离散单元之间场量传递的特点，在TM波情形下推导了DGTD各向异性完全匹配层吸收边界中的迭代计算式，实现了波在UPML层中的衰减．仿真算例说明，文中给出的DGTD UPML吸收边界对电磁波的双重衰减达 130 dB，吸收效果良好，满足二维情形电磁场精确仿真的需求．

[1] 王林年, 褚庆昕, 梁昌洪. 交替方向隐式时域有限差分法中的Berenger理想匹配层[J]. 西安电子科技大学学报, 2006, 33(3): 458-461.

WANG Linnian, CHU Qingxin, LIANG Changhong. Berenger’s Perfectly Matched Layer for the Alternating Direction Implicit Finite-difference Time-domain Method[J]. Journal of Xidian University, 2006, 33(3): 458-461.

[2]姜彦南,葛德彪,杨利霞.卫星模型散射FDTD计算的共形边界研究[J]. 西安电子科技大学学报, 2007, 34(4): 587-589.

JIANG Yannan, GE Debiao, YANG Lixia. Conformal Boundary Scheme in FDTD Computation of Satellite Model Scattering[J]. Journal of Xidian University, 2007, 34(4): 587-589.

[3]BERENGER J P. A Perfectly Matched Layer for the Absorption of Electromagnetic Waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200.

[4]CHEN J, LIU Q H. Discontinuous Galerkin Time-domain Methods for Multiscale Electromagnetic Simulations: a Review[J]. Proceedings of the IEEE, 2013, 101(2): 242-254.

[5]ALVAREZ J. A Discontinuous Galerkinfinite Element Method for the Time-domain Solution of Maxwell Equations[D]. Granada: University of Granada, 2013: 31-39.

[6]XIAO T, LIU Q H. Three-dimensional Unstructured-grid Discontinuous Galerkin Method for Maxwell’s Equations with Well-posed Perfectly Matched Layer[J]. Microwave and Optical Technology Letters, 2005, 46(5): 459-463.

[7]STYLIANOS D, LEE J F. Interior Penalty Discontinuous Galerkin Finite ElementMethod for the Time-dependent First Order Maxwell’s Equations[J]. IEEE Transactions on Antennas and Propagation, 2010, 58(12): 4085-4090.

[8]PENG D, CHEN L, YIN W L, et al. An Efficient DGTD Implementation of the Uniaxial Perfectly Matched Layer[C]//Proceedings of the 2013 International Symposium on Antennas & Propagation: 2. Piscataway: IEEE, 2013: 1272-1275.

[9]JI X, CAI W, ZHANG P. Reflection/Transmission Characteristics of a Discontinuous Galerkin Method for Maxwell’s Equations in Dispersive Inhomogeneous Media[J]. Journal of Computational Mathematics-international Edition, 2008, 26(3): 347-364.

[10]NIEGEMANN J, KÖNIG M, STANNIGEL K, et al. Higher-order Time-domain Methods for the Analysis of Nano-photonic Systems [J]. Photonics and Nanostructures-Fundamentals and Applications, 2009, 7(1): 2-11.

[11]GEDNEY S D, KRAMER T, LUO C, et al. The Discontinuous Galerkin Finite Element Time Domain Method (DGFETD)[C]//IEEE International Symposium on Electromagnetic Compatibility. Piscataway: IEEE, 2008: 1-4.

[12]JIN J M. The Finite Element Method in Electromagnetics [M]. 3rd Edition. New York: John Wiley &Sons, 2014: 37.

(编辑：齐淑娟)

Implementation of UPML absorbing boundary conditions in DGTD method

LILinqian1,2，WEIBing1,2，YANGQian1,2，GEDebiao1,2

(1. School of Physics and Optoelectronic Engineering, Xidian Univ., Xi’an 710071, China; 2. Collaborative Innovation Center of Information Sensing and Understanding, Xidian Univ., Xi’an 710071, China)

For the DGTD-UPML absorb boundary condition,the basic theory of UPML in the TM case is studied and implementationis presented. By lessons from the ideas of impedance matching, anisotropic parameters set and matched matrix in the FDTD method, based on the characteristics of the unstructured meshing and features of flux transfer among the elements, the formulas for wave propagation in the UPML are presented, and then the iterative formulas are derived. Compared with the generalreflectivity of -24 dB in the first step SMABC due to the discretization of the unstructured grid in the DGTD, the double attenuation of 130 dB demonstrates the good absorption of the 2D UPML layer for the electromagnetic wave.Key Words: discontinuous Galerkin time domain(DGTD); uniaxial anisotropy perfectly matched layer(UPML); TM wave

2015-10-05

时间：2016-04-01

国家自然科学基金资助项目(61231003，61571348，61401344)

李林茜(1985-)，男，西安电子科技大学博士研究生，E-mail: 395106835@qq.com．

魏 兵(1970-)，男，教授，E-mail: bwei@xidian.edu.cn．

http://www.cnki.net/kcms/detail/61.1076.tn.20160401.1622.030.html

10.3969/j.issn.1001-2400.2016.06.015

O441.4

A

1001-2400(2016)06-0086-05