基于灰色BP神经网络组合模型的深基坑周围地表沉降预测研究

刘 戈，仝国柱

（天津城建大学 土木工程学院，天津 300384）

土木工程

基于灰色BP神经网络组合模型的深基坑周围地表沉降预测研究

刘 戈，仝国柱

（天津城建大学 土木工程学院，天津 300384）

在深基坑工程施工过程中，基坑周围地表的沉降对周围建筑物、地下管线和支护体系的安全都会造成很大的影响，如何利用对影响基坑周围地表沉降的关联因素的研究并结合基坑周围地表沉降的监测数据来分析得到基坑周围地表沉降量的走势，已成为城市建设中的一个重要的安全课题.以天津市某换乘车站为例，分析影响该基坑周围地表沉降的关联因素，建立灰色预测和BP神经网络组合模型，在“小样本、贫信息”的情况下，得到的预测结果与实际监测值吻合度较高.利用该预测模型可对一些在开挖过程中监测天数相对较少的深基坑工程进行可靠而准确的预测.

深基坑；灰色BP神经网络组合模型；地表沉降

深基坑工程施工过程中由于受到周围交通和施工场地影响，使得施工条件受到一定限制，施工风险进一步增加.按照信息化施工的要求，在深基坑开挖过程中要进行基坑监测，并根据监测结果对深基坑的监测控制指标进行分析预测［1］.在这种情况下，如何充分利用有限的监测数据和现场巡视信息对深基坑工程进行全面的安全风险预测，并对潜在的安全风险做好应对措施，已成为深基坑工程信息化施工亟待解决的问题.

天津地处沿海软土地区，深基坑开挖必将引起周围土体的沉降变形，基坑周围地表沉降监测是项目深基坑工程监测重点之一.为了对深基坑周围地表沉降量的预测在监测天数较少的情况下依然能够得出精度较高的结果，选用灰色 BP神经网络组合模型进行预测分析.灰色 BP神经网络组合模型是在传统的灰色GM（1，1）模型和BP神经网络模型的基础上，结合了这两个传统预测模型的优势，减小了 BP神经网络在训练过程中由于监测数据点的误差较大而给结果造成影响，也满足 BP神经网络对样本需求量较大的特点［2-3］.同时利用 BP神经网络的适应学习功能、误差可控的特点，能克服灰色预测模型对预测结果不可控的缺点［4］.

本文灰色 BP神经网络模型基于已有的深基坑监测数据，对未来三天基坑周围地表的各监测位点的走势进行预测，以 DBC-01-3点位为例进行定量分析，并通过实际值和预测值比较，验证了该模型对预测基坑周围地表沉降量是可行的，为今后深基坑开挖地表沉降量的有效预测提供帮助.

1 工程概况

天津地铁鞍山西道站位于红旗路和鞍山西道交叉口，周围交通流量比较大，因此对基坑周围土体的沉降要求较高.车站采用明挖法施工，主体二层结构，局部换乘段为三层.基坑标准段深度约16.76，m，宽度为 22.70，m；盾构井段深度约18.73，m，宽度为 27.30，m；换乘节点段深度约为24.22，m，宽度为 24.70，m.侧墙采用围护结构及内衬墙间夹柔性防水层的复合墙结构.围护结构为0.8，m厚地下连续墙，换乘节点段采用1.0，m厚地下连续墙.车站计算站台中心位置顶板覆土厚度约3.00，m.施工现场北侧监测点位平面布置如图1所示.

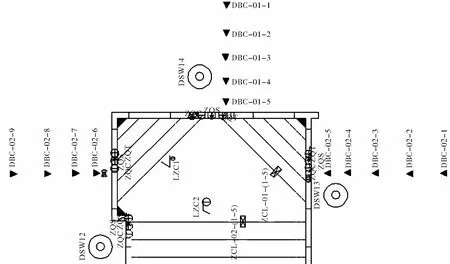
图1 施工现场北侧监测平面

2 深基坑施工过程中周围地表沉降的关联因素分析

影响深基坑施工过程中周边地表沉降的因素有环境因素、设计因素和施工因素.其中环境因素包括土层特征、地下水位及分布、周围建筑和交通状况等；设计因素包括基坑形状、开挖深度、挡土结构的选择、支撑系统应力预加方法、永久结构施工方法等；施工因素包括施工顺序、基坑降水、基坑开挖顺序及方法、挡土结构的密闭性、支撑系统的安装与拆除、预应力的施加时间与大小、土的回填等［5］.

天津市地处沿海地区，沉积层厚度较大，其间发育多层承压含水层，各含水层又以透水性很弱的黏性土层分隔［6］.该工程地下含有两层不同深度的承压含水层，第一承压含水层被地连墙隔断，为防止第一层承压水造成坑底隆起、土体沉降等问题，需对坑内潜水和第一层承压水做疏干处理.第二承压含水层距离基坑底部10，m范围内，需对该承压水进行抗突涌稳定性验算，并严格按照“按需降水、分层降水、动态调整”的原则适当抽取承压水，降低承压含水层的水头，确保项目基坑开挖的安全［7-8］.故本文选取 DSW14监测点的水位变化作为地表沉降的关联因素之一.

深基坑在开挖过程中，支护结构的变形主要表现为侧向和竖向位移.该深基坑工程开挖方法为先撑后挖，第一道混凝土支撑首先架设，在忽略第一道支撑的轴向变化量的情况下，墙顶水平位移变化较小.随着开挖深度的增加和钢支撑的架设，墙顶的水平位移不会再有明显的增加，墙身中部向坑内凸出，最大水平位移发生在基坑开挖面附近，且随开挖深度的增加逐渐向坑底移动［9］.Mana & Clough（1981）通过对工程实测数据分析表明：归一化的墙体横向位移最大值与坑外地表沉降最大值存在一定的比例关系，这也就说明坑外地表的变形同墙体的位移存在着紧密的联系［10］.所以经分析，本文选取 ZQT（16）监测点-5.5，m处的水平位移作为地表沉降的关联因素之一.

综上所述得出，影响地表沉降的关联因素为坑外地下水位相对深度和围护结构的侧移.

3 灰色BP神经网络预测模型

3.1 灰色BP神经网络模型的建立

首先，对深基坑施工过程中周围地表沉降的关联因素的原始数据进行一次累加，得到相应的累加数列来弱化原始数据序列的随机性；然后，通过建立灰色预测模型计算出该序列可能的变化趋势；再用灰色系统对关联因素的预测结果作为 BP神经网络的输入样本值，用地表沉降的实测值作为 BP神经网络的输出样本值，通过对 BP神经网络的训练，得出用于预测深基坑周围地表沉降的 BP神经网络模型［11-12］.建模步骤如下.

（1）对两组原始数据分别进行一次累加，得到一次累加序列，经过最小二乘法估计模型的系数向量a，将系数向量带入下列公式

得到 GM（1，1）模型的时间响应函数（预测模型），即

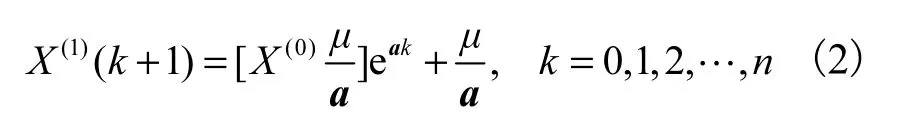
模拟计算后进行残差分析，看是否满足要求，若不满足，修正残差后重新计算，若满足则逐步计算得出之后十五天内各自对应的预测值［13］.

（2）将灰色 GM（1，1）模型所得到的两组预测数据（2014-05-15至 2014-06-14的预测值）作为三层神经网络的输入训练样本，取对应的实际地表沉降数据组成数据序列作为神经网络的输出，通过不断地修改各层的权重及阈值，使得误差函数逐渐减少，最终达到预计的效果.

（3）使用第（1）步中得到的两个关联因素之后几天内各自的预测值作为第（2）步中已训练好的神经网络的输入，所得预测结果即为本次灰色 BP神经网络组合模型的预测结果，并且对该结果与检测样本中实测值进行比对检验［14］.

3.2 利用灰色预测 GM（1，1）对两组关联数据进行预测分析

根据3.1中的灰色预测模型，DSW14监测点水位变化量（初始值为 2.051，m）的监测数据和 ZQT（16）监测点-5.5，m处水平位移的监测数据，利用Matlab软件编写预测代码，对2014-05-15到2014-05-29内相应点位的变化量进行计算得到相应点位的时间影响函数；利用得到的时间响应函数对之后一天的变化量进行预测，并进行残差分析.然后使用因子替换的方法，不断将新得出的预测值替换到模型中去（例如：｛X0（1），X0（2），…，X0（n）｝，当预测得到时，就用替换X0（1）得到，分别得到相应序列的时间响应函数，并对之后一天的变化量进行预测.最终计算得出之后十五天（2014-05-30至2014-06-13）内各自对应的预测值（见表1）.

表1 DSW14、ZQT-16（-5.5，m）监测点位的GM（1，1）预测值

通过上述灰色预测模型的计算分析，得到相关点位的预测值及残差分析值.在利用 GM（1，1）模型对地下水位进行预测时，地下水位的变化量受空气湿度、降雨和各降水井抽水量的影响较大.比如，表1中 DSW14监测点水位的变化量，受降雨的影响，2014-06-03、2014-06-08、2014-06-09、2014-06-10这几天的残差分析值都大于 10%，这时的预测值就会产生较大的误差.所以，在受外界因素影响时，其残差分析的标准要在原始参考标准的基础上相应增大.这里用 GM（1，1）模型对水位进行预测，主要目的是为了消除监测点水位变化量受外界因素的影响，从而得到一组在正常天气环境下该监测点位的变化量，为之后利用 BP神经网络模型对深基坑开挖过程中周围地表沉降量的预测提供一组比较可靠的相关数据.

3.3 BP神经网络模型的建立及训练

该网络模型利用非线性的神经元处理函数，通过前期对大量输入数据的学习训练，将学习内容记忆到网络中去，从而实现从输入到输出的复杂非线性映射.BP神经网络的学习过程由正向计算过程和误差逆传播过程组成，通过不断地调整阈值和连接权值大小，模型对输入数据响应的精确度不断提高，使得误差被控制在允许的误差范围之内，从而实现自动收敛［15-16］.

3.3.1 BP神经网络模型的数学描述

BP神经网络模型的第一步是将输入信号先向前传播至隐含的节点上，经过激活函数之后，再把隐含节点上的输出信息传送到输出节点，最后在输出节点输出结果.第二步是反向传播的过程，若在输出层未能获得期望的输出值，则逐层递归计算出实际输出和期望输出之间的差值，以便根据此差值调节权值.最终针对每一权重值计算得到发送单元的激活值和接收单元的误差值的乘积.隐含节点的激活函数一般选取标准的 Sigmoid型函数.模型结构如图2所示.BP算法的数学表达式如下［17］.

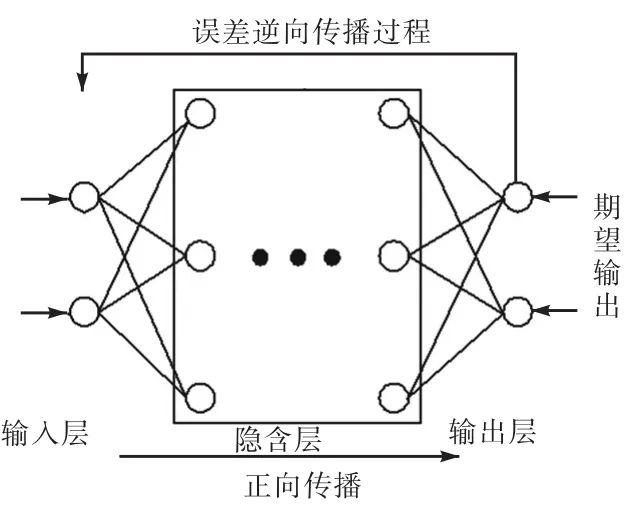
图2 BP神经网络模型结构

正向传播数学表达式：节点j的输入信息为

节点j的输出值为

反向传播时数学表达式：BP神经网络的期望输出dk和实际输出值ojk差值的平方和作为目标函数如下式

式中：m为输出层神经单元的数目.

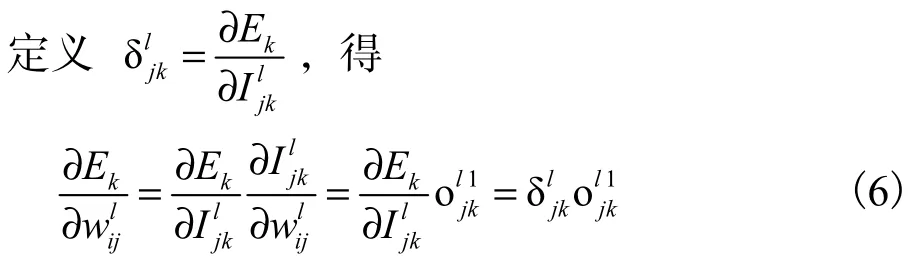
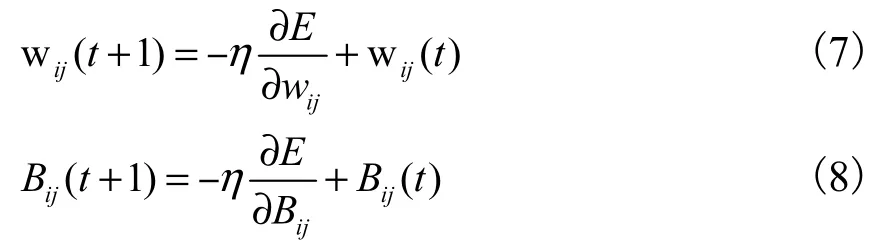
直到N个样本总误差满足精度要求，即

式中：ε 是精度.

3.3.2 利用BP神经网络模型进行预测分析

根据上节给出的 BP神经网络模型的数学表达式，利用3.2中灰色预测模型GM（1，1）对DSW14监测点 2014-05-15到 2014-06-13水位变化量（初始值为 2.051，m）和 ZQT（16）监测点-5.5，m处水平位移两个关联因素的预测数据作为模型的输入，基坑周围地表实际沉降值作为输出（见表2），对BP神经网络模型进行训练.设置 BP神经网络模型在基坑周围地表沉降预测时的各个参数值：输入维度为2维；输入样本数为 30个；训练循环次数为 100次；目标误差为 0.001；权值和阈值设定在（-1，1）区间内随机取值.利用Matlab软件编写预测代码进行预测计算，将利用灰色预测模型 GM（1，1）对DSW14监测点2014-06-14到2014-06-16水位变化量（初始值为2.051，m）和ZQT（16）监测点-5.5，m处水平位移大小作为模型的检测输入数据（见表3），得到预测结果（见表4）.

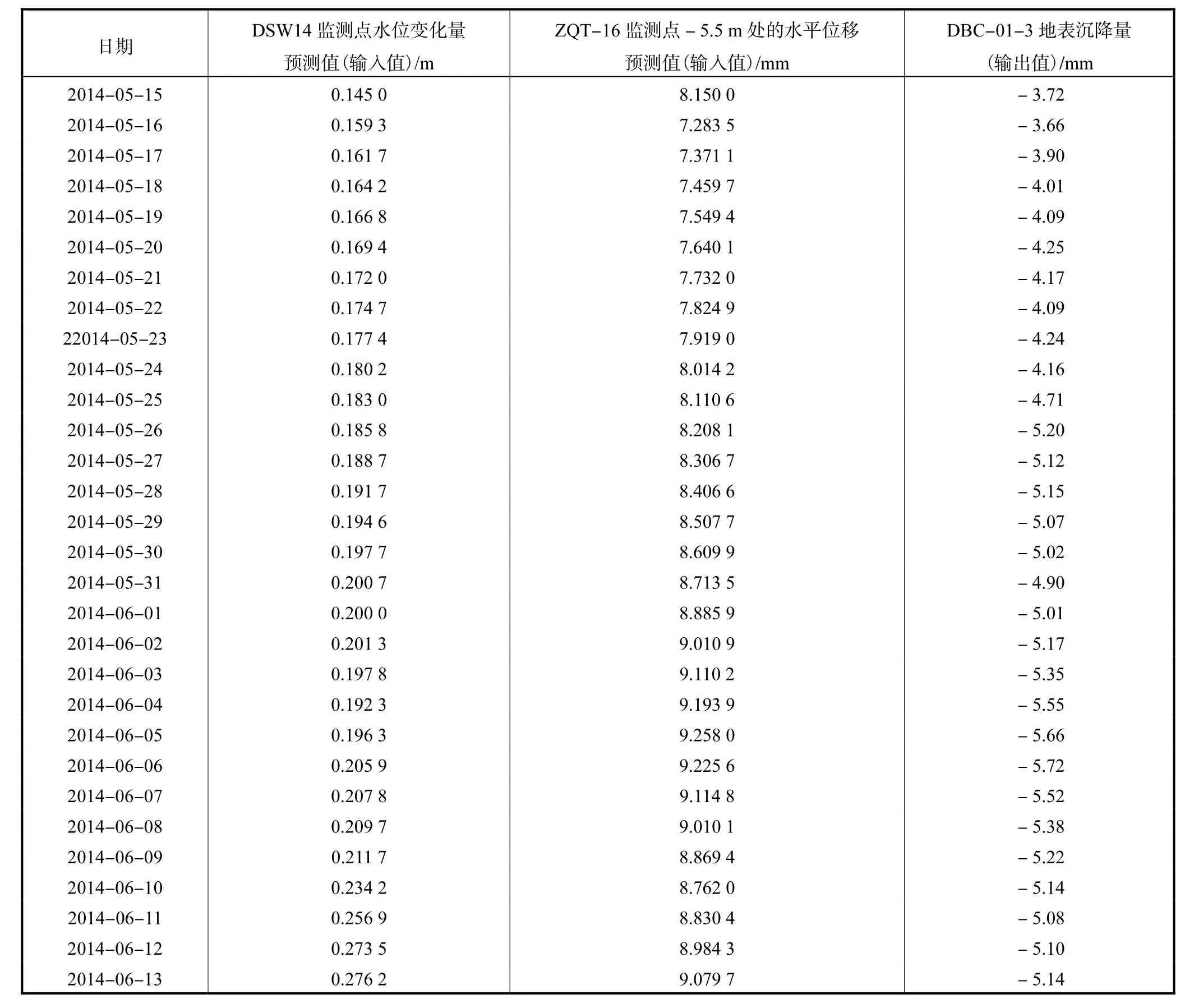
表2 BP神经网络模型的输入、输出数据

表3 预测模型的具体检测输入数据

表4 DBC-01-3地表沉降量在不同方法下的预测结果

由表4可知，在相同的数据条件下，灰色 BP神经网络组合模型预测分析得到的结果与实际值相比吻合度较高，且较灰色预测 GM（1，1）模型误差率更小，表明使用灰色 BP神经网络组合模型在深基坑施工过程中对基坑周围地表沉降值进行预测分析是可行的.

4 结 论

（1）利用灰色 BP神经网络组合模型对少量实测数据进行预测分析比灰色预测模型的预测精度更高，可为工程在施工过程中提前预知安全隐患并做好预防措施提供有效的帮助.

（2）该模型既能够保持灰色预测在短期预测时高精度的优点，又突出了 BP神经系统的学习能力强、误差可控的特性，而且满足了利用 BP神经网络进行预测时对训练数据较多的需求.利用灰色神经系统模型可以实现在“少样本、贫信息”的情况下对深基坑周围地表沉降量的走势进行准确分析.最终为深基坑各监测点位监测值的预测分析提供一种有效的研究方法.

（3）由于在深基坑施工过程中影响基坑周围地表沉降的关联因素有很多，此处只是结合该工程的实际情况选择了水位的变化量和支护结构水平位移这两个最主要因素作为关联因素.本文只是提出了一种施工方法，实际应用时，对于不同的监测点位，应选择相对应的关联因素进行有效的预测分析.

［1］刘勇健，李彰明.基于遗传-神经网络的深基坑变形实时预报方法研究［J］.岩石力学与工程学报，2004，3（6）：1010-1014.

［2］张伟丽.灰色系统理论在基坑变形预测中的应用［J］.莱阳农学院学报，2003（1）：60-61.

［3］张树光，张向东，李永靖.基坑周围地表沉降的人工神经网络预测［J］.辽宁工程技术大学学报（自然科学版），2001，6（5）：767-769.

［4］王旭东，赵建平，余 闯，等.人工神经网络在深基坑变形预测中的应用［J］.南京工业大学学报，2002， 24（5）：73-76.

［5］李守涛，刘宗仁，杨力良.深基坑开挖周边土体沉降形态的模拟研究［J］.低温建筑技术，2007，29（1）：103-105.

［6］徐新光.天津市某深基坑分步开挖对支护结构影响的现场监测及有限元分析［D］.天津：天津大学，2012.

［7］史佩栋.深基坑工程特殊技术问题［M］.北京：人民交通出版社，2004.

［8］陶书煜.基坑降水引起的地表沉降及围护结构位移分析［D］.北京：北京交通大学，2012.

［9］吴立新.基于神经网络的深基坑变形预测研究［D］.天津：天津城建大学，2013.

［10］ADBULAZIZ I M，CLOUGH G W.Prediction of movement for braced cuts in clay ［J］.Journal of Geotechnical Division，1981，107（GT6）：759-777.

［11］刘 戈，吴立新.基于 BP神经网络法对地连墙后土体沉降预测分析：以天津地铁施工为例［J］.沈阳建筑大学学报（自然科学版），2013（5）：834-840.

［12］贾 备，邬 亮.基于灰色 BP 神经网络组合模型的基坑变形预测研究［J］.隧道建设，2009，29（3）：280-284.

［13］张 丽，白雪莲.灰色神经网络耦合模型在河套灌区引黄水量预测中的应用［J］.安徽农业科技，2012，40（1）：597-599.

［14］罗 云.深基坑监测及基于神经网络的变形预测研究［D］.西安：西安建筑科技大学，2007.

［15］齐 干，朱瑞钧.基于 BP 网络的基坑周围地表沉降影响因素分析［J］.地下空间与工程学报，2007，3（5）：863-867.

［16］彭 涛，杨岸英，梁 杏，等.BP 神经网络-灰色系统联合模型预测软基沉降量［J］.岩土力学，2005，26（11）：1810-1814.

［17］李 燕.基于 BP神经网络的深基坑围护变形预测［D］.杭州：浙江工业大学，2013.

参考文献：

［1］罗玲玲.POE研究的国际趋势与引入中国的现实思考［J］.建筑学报.2004（3）：82-83.

［2］王建武.基于 POE研究的校园开放空间改造性规划——以北京大学为例［J］.2007（5）：77-82.

［3］白 骏.建筑使用后评价程序和方法研究［D］.北京：北京建筑工程学院，2003.

［4］王祖纬.城市开放空间使用后评价方法研究［D］.太原：太原理工大学，2008.

［5］马婷慧，哈尔滨金河湾湿地公园 POE调查及优化策略研究［D］.哈尔滨：哈尔滨工业大学，2012.

［6］杨·盖尔.交往与空间［M］.何人可，译.北京，中国建筑工业出版社，2002.

［7］朱小雷.建成环境主观评价方法［M］.南京：东南大学出版社，2005.

［8］克莱尔·库珀·马库斯，卡罗琳·弗朗西斯.人性场所——城市开放空间设计导则［M］.俞孔坚，译.北京：中国建筑工业出版社，2001.

Public Space Survey Research on Residential Community in New Town Based on POE：Taking Tianjin Zhangjiawo Town as an Example

WANG Jing，XIAO Yu，LÜ Yongquan
（Schoot of Architecture，TCU，Tianjin 300384，China）

Post Occupancy Evaluation means empirical investigation of users’ appraisal to building Environment.This paper is a site investigation to public space of Zhangjiawo residential community，using the method of Participatory observation，interviews，questionnaires to collect the data，analyzes the questionnaire results with Excel and SD Curve Analysis，generalizes the users’ basic attributes，behavior characteristics，the way of communion to sum up the problems，and puts forward proposals on the missing of geographical features and the passive of seasonal changes and so on.

new town；public space；post occupancy evaluation；Zhangjiawo community

TU473.2

A

2095-719X（2016）03-0184-06

2015-06-01；

2015-10-30

天津市建委重点项目（2010软-11）

刘 戈（1977—），男，天津人，天津城建大学教授，博士.