基于UFD理论的致密气藏分段压裂优化

时 贤，张凯奥，程远方，李友志，张矿生

(1.中国石油大学，山东 青岛 266555；2.中海油研究总院，北京 100028；3.中国石油长庆油田分公司，陕西 西安 710000)



基于UFD理论的致密气藏分段压裂优化

时 贤1，张凯奥1，程远方1，李友志2，张矿生3

(1.中国石油大学，山东 青岛 266555；2.中海油研究总院，北京 100028；3.中国石油长庆油田分公司，陕西 西安 710000)

考虑油藏物性和投资约束，提出基于UFD理论实现物理和经济产能双重最优的致密气藏水平井分段压裂优化设计思路。应用表明：裂缝内的支撑剂质量影响最佳支撑缝长、缝宽和导流能力等参数；净现值(NPV)和投资回报率(DROI)的高低与压裂横向裂缝数量密切相关，NPV值会随裂缝条数的增加而增加，DROI值则随着裂缝数量的增加而降低；NPV值和DROI值均具有随时间先升高，达到最高值之后再随时间逐渐下降的一般规律；相同泄流面积下，裂缝条数的优势将随生产时间的增长而表现出更明显的压裂经济效益。该套压裂优化方法和理论成果将对确保致密气水平井压裂效果的长效性和经济性提供可靠技术支撑。

致密气；UFD理论；水平井；分段压裂；经济优化；苏里格气田

0 引 言

应用水平井分段压裂技术进行储层增产改造是目前致密气藏高效开发的核心手段[1]。目前北美油藏体积改造理念已从片面追求增大储层改造规模转向寻找储层特征和压裂技术相匹配的经济压裂模式，并更强调投入与产出的经济效益对比，希望通过合理参数的匹配，实现技术、风险和效益间的平衡。水力压裂优化经典思路通常将最大采油指数或经济效益设为目标函数，再通过油藏数值模拟，建立多目标函数实现压裂效果的优化。实际应用表明，该方法更适用于中高渗储层，且计算复杂，由于依靠提升支撑剂用量来增加裂缝长度实现经济最优，因此，结果常脱离储层实际。UFD(Unified Fracture Design)理论则是针对低渗透储层压裂优化的另一思路。该方法认为在支撑剂体积固定的条件下存在最佳无因次裂缝导流能力，可以此来优选匹配储层性质的裂缝长度和宽度，但该方法也忽视了储层和经济条件的实际限制[2-3]。为此，通过UFD理论优化和三区产能模型结合计算水平井分段压裂最大物理产能，再通过经济评价寻找最佳经济效益下的水平井分段压裂施工规模，实现经济最优。该套压裂优化设计方法充分考虑了油藏地质参数、经济参数、压裂施工规模，可实现产量和净现值的最大化，约束条件的引入使结果更具实际意义，对致密气水平井分段压裂生产潜力分析和压裂施工开发方案的制订具有重要价值。

1 UFD方法原理

UFD压裂设计核心是通过支撑剂指数决定给定油藏能达到的最大无因次生产指数，并同时取得最大无因次裂缝导流能力，再计算出相应的最佳长度和宽度组合[4]。受地层条件下的应力载荷作用、压裂后破胶及裂缝内气体的非达西渗流等因素的综合影响，裂缝的渗透率会受到较大伤害，为考虑压裂效果的长效性，通常选取有效闭合压力中间值对应的裂缝渗透率，即有效渗透率作为初始设计参数。由于水平井分段压裂过程中形成的泄气区域存在形状差异，因此，矩形泄气区域条件下的改进支撑剂指数Np定义为[5]：

(1)

式中：Np为支撑剂指数；Kf-eff为有效裂缝渗透率，10-3μm2；K为基质渗透率，10-3μm2；Kf为裂缝渗透率，10-3μm2；Vp为泵入支撑剂体积，m3；Vres为气藏体积，m3；xf为裂缝单翼缝长，m；xe为矩形泄气区域长度，m；ye为矩形泄气区域宽度，m；w为平均裂缝缝宽，m；Ix为穿透比；CfD为无因次裂缝导流能力；h为裂缝高度，m。

其中，支撑裂缝渗透率和无因次最优导流能力表达式可见文献[4-5]，利用不渗透边界下Daal影响函数和Dietz不规则形状压力分布因子之间的关系，通过等效支撑剂指数可计算矩形泄气区域条件下的无因次采油指数[6]。在最优无因次裂缝导流能力值确定后，可通过如下关系计算最佳裂缝长度和宽度组合：

(2)

(3)

式中：xfopt为最佳裂缝长度，m；wopt为最佳裂缝宽度，mm；CfDopt为最优无因次裂缝导流能力。

2 致密气藏多层水平井分段多簇压裂产能预测模型

2.1 物理模型

致密气藏由于埋藏较深，一般层系较多且复杂。以美国Bakken致密气储层为例，Bakken组包括上部页岩、中部粉砂质白云岩和砂岩互层、下部页岩3个部分。通过基于厚度的加权平均法对薄互层的渗透率进行直接表征将存在较大误差，为此采用可动流体体积法对薄互层的平均渗透率进行计算。在纵向上分为i个渗透层的储层整体渗透率可通过下式计算得到：

(4)

式中：KH为油藏整体渗透率，10-3μm2；Ki为油藏垂向分布第i个层的渗透率，10-3μm2；i为不同渗透率的分层个数。

2.2 数学模型

根据水平井分段压裂井生产时的压降规律，在计算致密气产能时，将流动阶段划分为：未压裂改造区域的径向流、裂缝改造区域的线性流以及裂缝内的线性流。其中，最后的一个渗流阶段可细分为裂缝内的线性流和近井筒区域的径向流。在获得上述边界条件后，可通过合适的模型计算任何油藏形状下的致密气产能结果。综合3个区域的水平井分段压裂产量，可得水平井分段压裂的三区产能计算公式[8-9]：

(5)

式中：pave为油藏平均压力，MPa；pwf为井底流压，MPa；JR、JL、Jr分别表示为油藏径向流、裂缝径向流和油藏线性流的采油指数。

需要注意的是，该产能模型中需要代入油藏整体渗透率进行计算。

3 经济评价方法

UFD方法仅能使物理产能最大化，若仅依靠于物理优化的结果，可选择增大裂缝的级数与改造规模来单纯增加产量，而正确做法在于将物理优化与经济评价相结合，从而获得经济最优的设计方案[10-11]。水平井压裂过程中涉及的压裂费用可分为压裂设备费用、附加作业费用、水马力费用、液体和支撑剂等压裂材料费用。净现值和投资回报率是常用的经济评价指标。NPV与DROI公式为：

(6)

式中：NPV为净现值，元；DROI为投资回报率，%；x为生产时间，a；Rx为年度收益(考虑税收、折旧后)，元；Cf为压裂施工的总费用，元；j为折现率，%。

Cf与单条横向裂缝的压裂液体积、单条裂缝的支撑剂质量与水马力费用、横向裂缝总条数相关。通常情况下，净现值越大，压裂施工方案越优。而投资回报率则反映了压裂施工的资金利用效率。

4 整体优化设计步骤

设计步骤：①根据支撑剂类型、压裂液破胶对支撑剂渗透率的损害情况以及邻井致密气非达西流动状况计算支撑剂有效渗透率；②输入储层参数、支撑剂质量和裂缝数量等参数求得最优无因次裂缝有效导流能力，得到最大无因次采气指数，再计算最优裂缝长度和裂缝宽度组合；③结合实际施工条件，如支撑剂粒径等参数对相关的裂缝长度和裂缝宽度进行修正[5]；④根据修正后重新计算出的缝长和缝宽，并根据提出的致密气藏产能模型计算最大物理产量，结合经济模型计算压裂经济参数NPV和DORI，获得最佳经济产量；⑤如果结果不满足要求，则重新输入支撑剂质量和裂缝条数，并重复上述操作，直到压裂施工满足设计要求。对于致密气藏而言，在支撑剂性质和裂缝条数固定的情况下，通过上述方法可计算裂缝最优导流能力、最优几何参数以及最高采气指数，再结合经济参数可获取最优经济产量。

5 实例应用与分析

以鄂尔多斯盆地苏里河气田为例，该区块目的层岩石类型以长石岩屑、砂岩岩屑和砂岩为主，砂体纵向多期叠置， 普遍发育3～5层。经过前期储层评价，认为该储层纵向可分为4层。具体相关数值模拟的输入参数见表1。

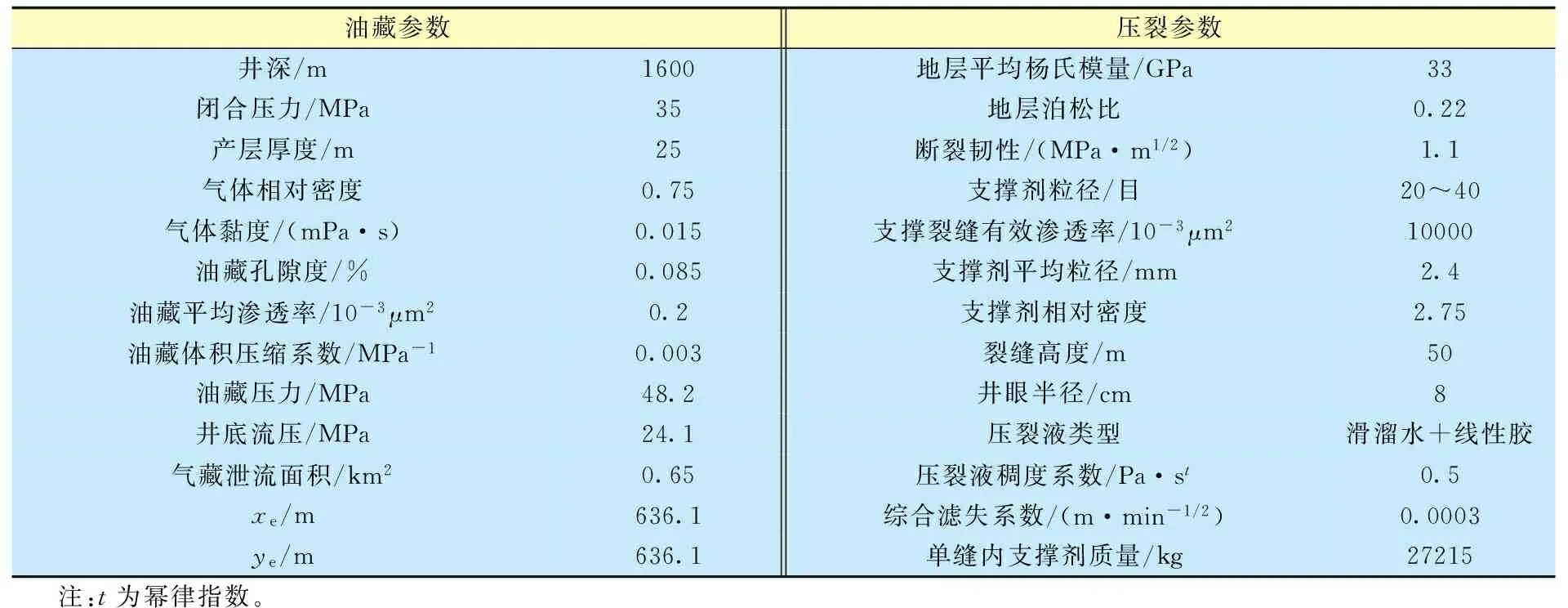
表1 油藏和支撑剂参数

输入表1中的参数，通过式(1)～(5)计算，可得到相关的最佳裂缝无因次导流能力、最佳半缝长、最佳缝宽等产能优化参数。考虑到裂缝宽度会影响支撑剂粒径的选择，一般要求炮眼直径大于 5.5 倍的支撑剂粒径，裂缝宽度大于2倍的支撑剂粒径，结合实际支撑剂粒径(约为2.4 mm)对裂缝的几何形态进行约束，得到更新后的裂缝参数(表2)。

通过计算，在支撑剂质量一定的条件下， 可确定裂缝条数和裂缝最佳几何形态的关系。由表2可知，随着横向裂缝条数的不断增加，最优裂缝长度先降低再增加，而最优裂缝宽度则先增加后降低，表现出相反的变化趋势。

表2 基于UFD优化后的裂缝相关参数

根据UFD优化后的裂缝参数和油藏参数，以20 a为生产时间，运用产能计算公式对水平井分段压裂产量进行计算，结果见图1。由图1可知，在支撑剂质量一定的条件下，裂缝条数越多，则最后的累计产气量越高，但当裂缝数量超过5条时，则增加幅度明显降低。

图1 裂缝日产气量、分段压裂累计产气量与生产时间的关系

天然气价格为4.5 元/m3，支撑剂价格为90 元/kg，钻井成本为2 400 元/m，压裂液价格和添加剂成本分别为11.75、8.00 元/m3，压裂设备损耗费为18 000 元/d，商业税和货币浮动率为5%，折现率为10%。根据式(6)计算NPV值和DROI值。图2、3分别为NPV值和DROI值的计算结果。由图2可知，计算NPV值随着横向裂缝的增大而逐渐增大，但增大趋势却逐渐减小，每条裂缝都存在最佳NPV值。实际NPV值受控于天然气价格、特殊储层性质、总开发成本以及油藏生产寿命等因素。DROI值随着生产时间的增长，表现出先增大后降低的趋势，之后则随着裂缝的增多表现出不同的变化规律，每条裂缝都存在其最佳DROI值。其中，除2条裂缝和3条裂缝的DROI值以外，DROI值皆随着裂缝条数的增加逐渐降低。

图2 NPV值与生产时间的关系

图3 DROI值与生产时间的关系

6 结 论

(1) 进行压裂效果的经济评价需要建立在相应的裂缝扩展模型、压裂井产能数学模型和压裂经济评价模型基础之上，同时借助相应的数学优化方法可得出最优的经济评价结果。研究压裂经济效益问题的本质是研究压裂优化问题，最优经济产能受控于泄流面积、天然气价格、储层油藏性质、总开发成本和油藏生产寿命等因素的综合影响。

(2) 由于考虑了实际油藏和施工经济条件的约束，致密气水平井分段压裂累计产气量结果更符合实际。从产能数值模拟结果来看，随着压裂施工年限的增加，最佳横向裂缝数量值减小，说明随着生产时间的增长，各条裂缝的泄流控制面积将逐渐增大。

(3) 泄流面积越大，在取得同样压裂效益时，所需的裂缝条数越多，但在进行压裂优化设计时需结合矿场实际条件及压裂设备和压裂材料类型综合考虑。该方法也可应用于致密油、页岩油气等其他非常规油气藏。

[1] 杨涛，张国生，梁坤，等.全球致密气勘探开发进展及中国发展趋势预测[J].中国工程科学，2012，14(6)：64-68.

[2] VALKO P P，ECONOMIDES M J. Heavy crude production from shallow formations：long horizontal wells versus horizontal fractures[C].SPE50421，1998：1-10.

[3] ECONOMIDES M，OLIGNEY R，VALKóP.Unified fracture design：bridging the gap between theory and practice[M].Texas：Orsa Press，2002：39-44.

[4] DAAL J A，ECONOMIDES M J.Optmization of hydraulically fractured wells in irregularly shaped drainage areas[C].SPE98047，2006：1-11.

[5] MARONGIU-PORCU M，ECONOMIDES M J，Holditch S A.Economic and physical optimization of hydraulic fracturing[C].SPE111793，2008：1-16.

[6] 郭建春，梁豪，赵志红.基于最优支撑剂指数法优化低渗气藏裂缝参数[J].西南石油大学学报(自然科学版)，2013，35(1)：93-98.

[7] GUO B，SCHCHTER D S.A simple and rigorous mathematical model for estimating inflow performance of wells intersecting long fractures[C].SPE38104，1997：645-659.

[8] RAHMAN M M，SARMA H K，YU H.Transverse fracturing of horizontal well-a unified fracture design to stimulate tight gas sands[C].SPE164013，2013：1-13.

[9] PORCU M M，WANG X，ECONOMIDES M J.Delineation of application and physical and economic optimization of fractured gas wells[C].SPE120114，2009：1-17.

[10] 李庆辉，陈勉，金衍，等.压裂参数对水平页岩气井经济效果的影响[J].特种油气藏， 2013，20(1)：146-150.

编辑 王 昱

10.3969/j.issn.1006-6535.2016.01.019

20150905；改回日期：20151115

国家自然科学重点项目“非常规天然气储层超临界二氧化碳压裂工程基础研究”(U1262202)及教育部长江学者和创新团队发展计划(RT1086)联合资助

时贤(1984-)，男，师资博士后，2007年毕业于中国石油大学(华东)电子信息工程专业，2014年毕业于该校油气井工程专业，获博士学位，现主要从事非常规油气及深水钻完井岩石力学等方面的研究。

TE357.12

A

1006-6535(2016)01-0087-05