一种面向动态发展系数a的新灰色预测模型

黄辉

（重庆工商大学 电子商务及供应链重庆市重点实验室，重庆 400067）

一种面向动态发展系数a的新灰色预测模型

黄辉

（重庆工商大学 电子商务及供应链重庆市重点实验室，重庆 400067）

既有灰色预测模型发展系数a是在满足原始序列模拟误差最小约束下，通过最小二乘法来求解的，当建模系列确定之后，发展系数a即随之确定，而缺乏与外部系统状态的同步变化，这是造成现有灰色模型性能不稳定的重要原因。文章通过离散灰色预测模型对发展系数a的动态性进行了研究，并在此基础上构建了一种发展系数a可动态变化的AGM(1，1)预测模型，最后应用该模型对我国天然气消费量进行了模拟及预测，且取得了较好的效果，从而进一步验证了基于动态发展系数a的新模型AGM(1，1)的有效性与实用性。

灰色预测模型；发展系数a；动态性；AGM(1，1)模型；天然气消费量预测

0 引言

预测是决策的基础。所谓预测，就是基于既有数据资料，分析系统发展规律或演化特征，并假定系统将按该规律或特征向前发展，在此基础上实现系统在未来某个时点发展趋势的预估。科学合理地分析系统发展历史规律是实现准确预测的基础，而假定系统将按既有历史规律发展则是实现有效预测的前提。预测通常只能处理常规性问题，对于非常规性突发事件，预测方法常常“失效”。比如，可以通过最近几年我国GDP发展趋势来推测我国在未来某年的GDP增长情况，但是如果期间发生战争或者大规模自然灾害，则所预测的GDP数据可能误差很大。预测分为定性预测和定量预测两类，前者主要通过经验推测或判断来实现，带有较大的主观性；后者通常数学方法来抽象和描述系统发展规律，并在此基础上实现预测，这类数学方法通常被称为定量预测模型。

以GM(1，1)为代表的灰色预测模型是灰色系统理论的核心，是处理“小样本、贫信息”不确定性预测问题的常用方法[1]，主要利用少量有效数据和灰色不确定性数据，通过序列的累加生成，揭示系统未来发展趋势[2，3]。现有灰色预测模型建模参数都是在满足原始序列模拟误差最小约束下，通过最小二乘法来求解的，换言之，当建模系列确定之后，模型参数随之确定，而且该参数贯穿于模拟与预测的整个过程[4-6]。在灰色理论中，对于相同的灰色预测模型，参数不变则模型不变；因此，现有灰色系统用一个恒定模型去模拟和分析不断变化着的复杂系统，其模拟可靠性与预测科学性难以得到有效保障，这是导致现有灰色模型模拟及预测精度不稳定的重要因素。本文尝试对GM(1，1)模型发展系数a的动态性进行研究，通过DGM(1，1)模型动态描述a的变化过程与发展态势，在此基础上构建一种发展系数a可动态变化的AGM(1，1)预测模型，最后通过应用该模型对我国天然气消费量进行了模拟及预测。

1 GM(1，1)模型基本概念

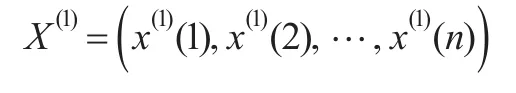
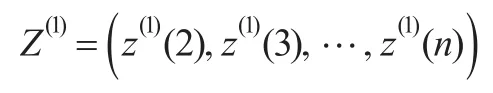
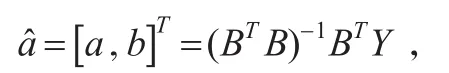
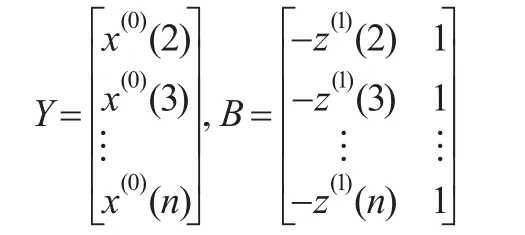
GM(1，1)模型x(0)(k)+az(1)(k)=b的时间响应序列为：

GM(1，1)模型x(0)(k)+az(1)(k)=b的还原值为：

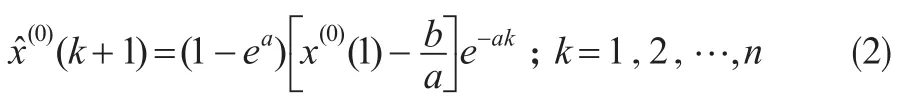
在GM(1，1)模型中，参数-a称为发展系数，其大小反映了(1)及(0)的发展态势；参数b称为灰色作用量，它反映了表征系统行为数据的变化关系，是从背景值挖掘出来的数据，其确切内涵是灰的。GM(1，1)模型的建模流程[1]如图1所示。

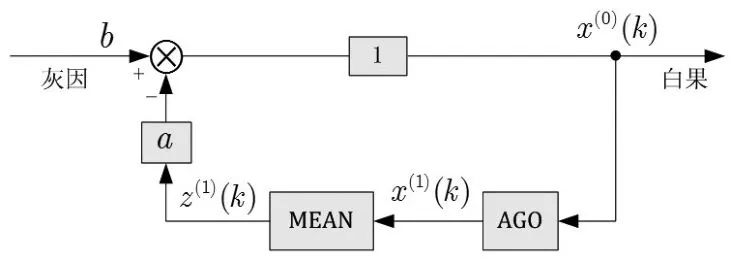
图1 GM(1，1)建模流程图

2 发展系数a的动态性及AGM(1，1)模型的构建

当k=2，3，…，n时，设GM(1，1)模型对应的发展系数为a2，a3…an，则根据GM(1，1)模型的基本形式可得：

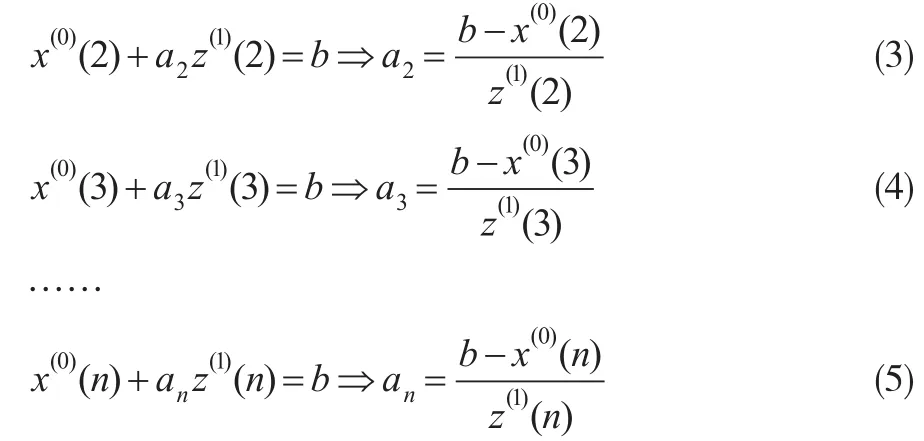
在公式(3)—公式(5)中，参数b为GM(1，1)模型的灰色作用量，x(0)(2)，x(0)(3)…x(0)(n)及z(1)(2)，z(1)(3)…z(1)(n)为建模数据，均为已知参数，因此可以计算得到GM(1，1)模型对应的发展系数a2，a3…an的值。设GM(1，1)模型对应的发展系数构成的序列为A=(a2，a3…an)，构建序列A的离散灰色预测模型（即DGM(1，1)模型），其时间响应序列及还原值分别为：

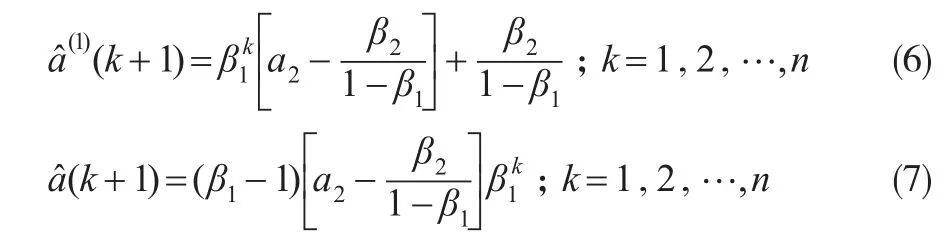
将通过DGM(1，1)模型动态模拟得到的GM(1，1)模型发展系数(k+1)代入公式(2)，从而实现GM(1，1)模型发展系数a的动态生成。则变化后的GM(1，1)模型为：

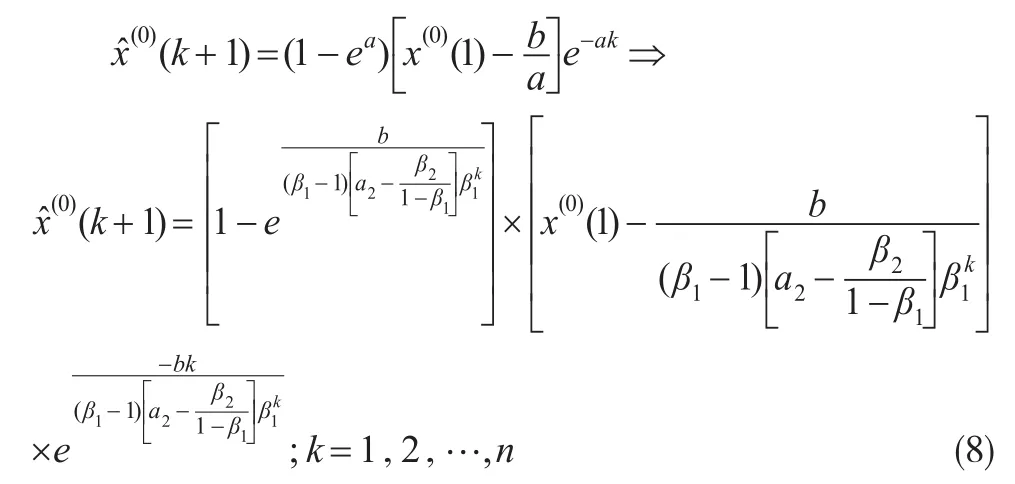
公式(8)称为发展系数a可调的动态GM(1，1)模型，简称AGM(1，1)模型。该模型通过离散灰色模型动态模拟发展系数a的变化趋势，进而实现了与外部系统的同步变化，理论上具有比静态发展系数a更高的模拟及预测性能。

3 模型应用与比较分析

本文采用AGM(1，1)模型模拟2006—2013年我国的天然气需求量，在此基础上对我国天然气需求量进行预测。2006—2013年我国天然气消费量如表1所示。

表1 2006—2013年我国天然气消费量（十亿立方米）

（1）参数b及发展系数A的计算

根据GM(1，1)模型参数的计算方法及公式(3)—公式(4)，可计算得AGM(1，1)模型的参数b及发展系数A，如下：

（2）DGM(1，1)模型参数β1及β2的计算

根据DGM(1，1)模型的建模机理及灰色系统建模软件，可计算DGM(1，1)模型参数β1及β2，如下所示：

β1=-0.0156，β2=-0.0782

（3）我国天然气消费量的模拟值及模拟误差

将计算得到的参数b及β1、β2代入公式(8)，可计算得2007—2014年我国天然气消费量的模拟值及模拟误差，如表2所示。

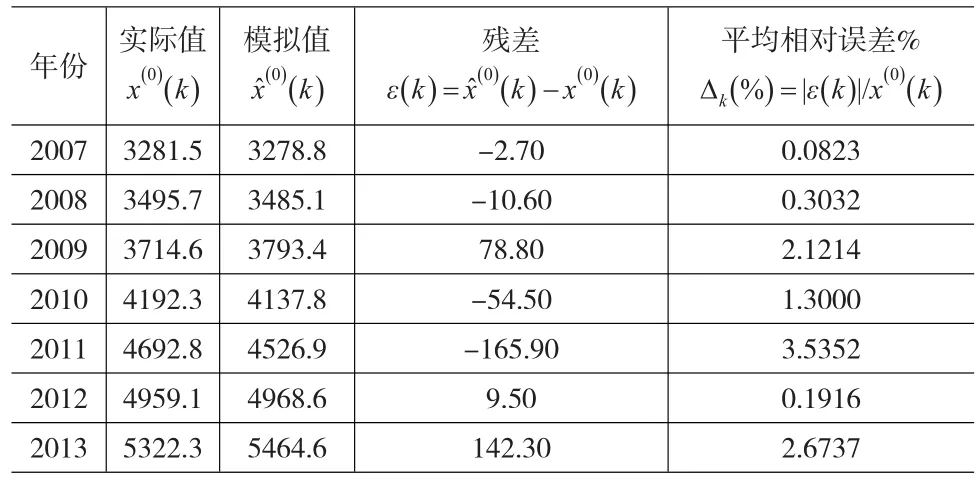
表2 基于AGM(1，1)模型的我国天然气消费量的模拟值、残差及平均模拟相对误差

根据表2可知，应用AGM(1，1)模型模拟2007—2013年我国天然气消费量的平均模拟相对误差为：

将表2中的Dk值代入公式(9)，可得

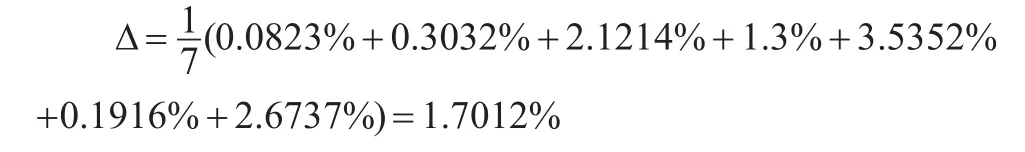
查灰色预测模型精度等级参照表可知，基于AGM(1， 1)模型的我国天然气消费量的平均模拟相对误差接近1级，可以用于预测。

（4）我国天然气消费量的预测

应用AGM(1，1)模型预测2014—2018年我国天然气消费量，如表3所示。

表3 2014—2018年我国天然气消费量预测数据（十亿立方米）

4 结论

现有的灰色预测模型建模参数都是在满足原始序列模拟误差最小约束下，通过最小二乘法来求解的，当建模系列确定之后，模型参数即随之确定，而且该参数贯穿于模拟与预测的整个过程。可见，现有的灰色建模方法用一个恒定模型去模拟和分析不断变化着的复杂系统，其模拟可靠性与预测科学性难以得到有效保障，这是导致现有灰色模型模拟及预测精度不稳定的重要因素。本文通过对GM(1，1)模型发展系数a的动态性进行研究，通过数学模型动态描述a的变化过程，在此基础上构建一种发展系数可动态变化的新灰色预测模型，并通过应用该模型对我国天然气消费量进行了模拟及预测，从而研究了新模型的模拟和预测性能。

[1]Deng J L.Introduction to Grey System Theory[J].The Journal of Grey System(UK)，1989，1(1).

[2]Wu L F，Liu S F，Cui W.Non-Homogenous Discrete Grey Model With Fractional-Order Accumulation[J].Neural Computing&Appli⁃cations，2014，25(5).

[3]Xie N M，Liu S F.Discrete Grey Forecasting Model and Its Optimiza⁃tion[J].Applied Mathematical Modeling，2009，33(2).

[4]仇世伟，刘思峰.GM(1，n)模型的离散化结构[J].系统工程与电子技术，2006，28(11).

[5]谢乃明，刘思峰.离散灰色模型的拓展及其最优化解[J].系统工程理论与实践，2006，(6).

[6]陈继光.区间灰数DGM(1，1)模型在负荷统计数据预测中的应用[J].统计与决策，2014，(7).

（责任编辑/易永生）

N941.5

A

1002-6487（2016）21-0019-03

国家自然科学基金资助项目（71271226）；教育部人文社会科学规划项目（14YJAZH033）；重庆市高等学校教学改革研究项目（1202010）

黄 辉（1965—），男，重庆人，教授，研究方向：管理科学定量方法。