基于植被指数比较的湿地区域LAI遥感估算研究
凌成星,鞠洪波,张怀清,孙 华
(1.中国林业科学研究院 资源信息研究所,北京 100091;2.中南林业科技大学 林业遥感信息工程研究中心,湖南 长沙 410004)
基于植被指数比较的湿地区域LAI遥感估算研究
凌成星1,鞠洪波1,张怀清1,孙 华2
(1.中国林业科学研究院 资源信息研究所,北京 100091;2.中南林业科技大学 林业遥感信息工程研究中心,湖南 长沙 410004)
以Worldview-2遥感影像作为数据源,对东洞庭湖湿地核心区域进行了LAI估算研究。首先对典型的植被指数与叶面积指数(VI-LAI)的相关性进行了分析;然后选择了7个与LAI之间存在显著相关性的植被指数(NDVI、RVI、DVI、SAVI、MSAVI、EVI、RDVI)作为VI-LAI的模型因子,采用多回归模型与LAI实测数据进行拟合分析,筛选出这回归模型的最优因子;然后利用实测数据作为检验样本,最终确立了以NDVI为模型变量的指数模型是用于LAI估测的最优模型,精度达到了74.34%。结果表明:本研究采用的多植被指数比较建立的湿地植被VI-LAI反演模型,是可以比较准确获取湿地区域叶面积指数特征的方法。
湿地;Worldview-2影像;植被指数;LAI估算
湿地是和森林、海洋同等重要的生态系统,兼备了陆生和水生生态系统的特点,非常特殊,所以也具有很多的生态功能。因其特殊的生物和水文条件,天然湿地具有较高的净初级生产力和较低的分解活性,是一个重要碳库。研究与湿地生态系统和碳储量等相关性非常强的湿地植被叶面积指数(Wetland LAI),同样也具有非常重要的意义。在植被叶面积指数估算研究方面,目前主要集中在统计模型和光学模型两个方面,研究对象也多为森林区域。光学模型方面利用LANDSAT-TM数据的植被指数法,研究NDVI等植被指数与不同龄级林分的叶面积指数相关关系[1-4]。在统计模型LAI叶面积指数反演研究中,有利用小型光谱成像仪数据构建LAI回归估测模型方面的研究[5],有采用有效叶面积指数进行遥感反演得到马尾松毛虫寄主特征[6],也有采用指数回归分析和线性回归分析等方法,分析了各种VIS数据与LAI的相关性[7-8],有一些经济林冠层光谱辐射特征也进行了研究[9]。随着高光谱遥感的发展,研究人员发现了将地面实测的高光谱数据和二向反射模型相结合,可提高森林LAI反演的精度[10-12]。在湿地区域开展植被的叶面积指数估算工作还并不是特别广泛,因此本研究拟采用多植被指数比较的方式,建立最优的估算模型,对湿地植被的叶面积指数进行估算,得到研究区叶面积指数分布特征,为研究湿地植被特征、湿地生物量分布等科学问题提供准确、合理的数据支持。
1 研究区概况
湖南东洞庭湖是“国际湿地公约”收录的由中国政府指定的国际重要湿地自然保护区之一,位于长江中下游荆江江段,湖南省东北部岳阳市境内,中心坐标为 28°59′52″N,112°59′52″E。湖区区域面积达2 500 km2,该区域地处亚热带湿润气候区,湿地类型和湿地植被都非常典型,日照充足,雨量充沛,有丰富的沉水、浮水和挺水植物。本研究选取了东洞庭湖湿地核心区域作为本项目的研究区(见图1),面积为455 km2,利用Worldview-2卫星数据进行叶面积指数估算研究。
2 LAI数据采集和多植被指数相关性分析
采取抽样法在研究区进行系统布点,根据不同样地植被类型、植被覆盖度、位置等参考因素进行样地选取,共选取92个测量样点,包括30个苔草样点、26个辣蓼样点、25个芦苇样点、11个泥蒿样点。研究区样点分布如图2所示。
(1)样地叶面积指数的测量
采用LAI-2000植物冠层分析仪来实现样地数据的采集(如图3所示)。首先在样地设置样方,大小为30 m×30 m,然后分别在每个样地的四个方向和中心点进行取值,用LAI-2000植物冠层分析仪分别对n号样地测量5次,获取LAI值Xn1、Xn2、Xn3、Xn4、Xn5,再取平均值为N号样地的LAI值,计算方法见公式(1)。
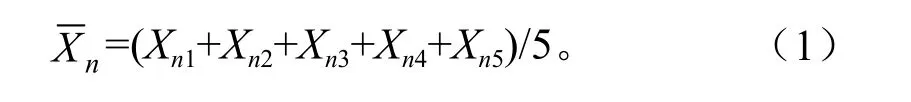

图1 研究区位置示意Fig. 1 Location of research area

图2 样地分布Fig. 2 Sample distribution map

图3 LAI-2000植物冠层分析仪Fig. 3 LAI-2000-Plant canopy analyzer
在每个样地中均匀布设5个叶面积指数测量点,并用GPS定位(见图4所示);连接叶面积指数仪的传感器后首先校准数据,设置分辨率为高分辨率;确认日期和时间的准确;设置叶面积指数仪的操作模式后启动测量程序;连续2次输入标记后开始测量,保持传感器水平;采集每个测量点的工作照片,以便和测量数据进行比对(见图5所示)。
(2)植被指数的计算
根据WORLDVIEW-2八波段多光谱特征,选取了7个特点不同植被指数进行分析,包括归一化植被指数(NDVI,x1)、比值植被指数(RVI,x2)、差值植被指数(DVI,x3)、土壤调节植被指数(SAVI,x4)、修正的土壤调节植被指数(MSAVI,x5)、增强型植被指数(EVI,x6)、重归一化植被指数(RDVI,x7),以此作为VILAI的经验模型因子(见表1)。

图4 外业调查叶面积指数数据表Fig. 4 Leaf area index of investigated data

图5 叶面积指数测量工作Fig .5 The Measuring work of leaf area index
(3)VI建模因子与LAI相关性分析
通过实测的92组样本数据,以不同样地植被类型、植被覆盖度、位置等参考因素,从4种湿地植被类型(苔草、辣蓼、芦苇、泥蒿)样地数据中选取了各类型四分之三的数据用来拟合VI-LAI的回归模型,其中包括了测量过程中的每种湿地植被类型样地数据中LAImax和LAImin数据,共有69组数据作为建模样本用于估测模型拟建,23组数据作为检验样本。把选取的NDVI、RVI、DVI、SAVI、MSAVI、EVI、RDVI这7个植被指数与叶面积指数进行相关性分析,得到结果如表2所示。

表1 7个植被指数计算模型Table 1 Calculation model of vegetation index
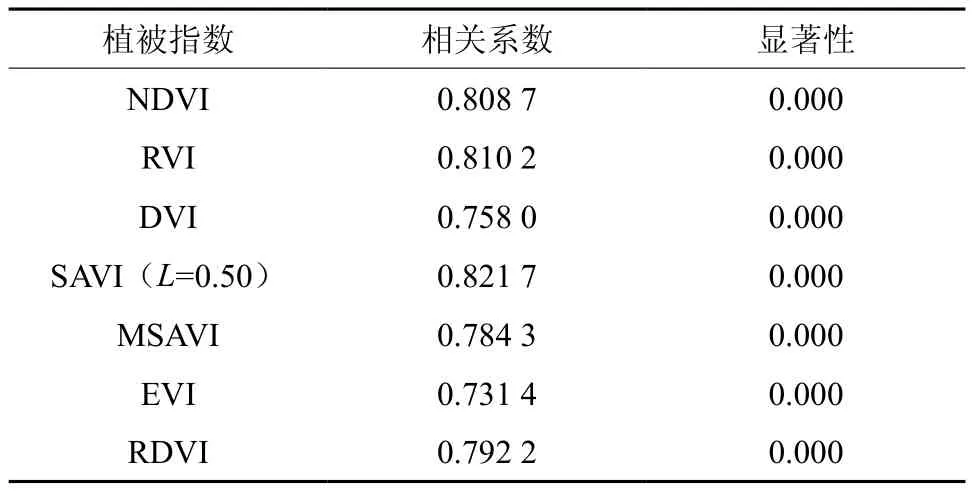
表2 7个植被指数与叶面积指数间相关性Table 2 Correlation between vegetation index and leaf area index
由表2可知:在建模样本数据中以相关性从大往小划分依次为SAVI> RVI>NDVI>RDVI>MSAVI>DVI>EVI,7个因子的显著性都不高,Sig值全部<0.01。
3 植被指数与叶面积指数(VI-LAI)回归模型构建和实现
为了实现对叶面积指数的有效估算,采用6种不同类型的一元统计回归模型(如表3所示)。

表3 回归模型Table 3 Regression models
(1)叶面积指数一元线性回归模型
将 NDVI、RVI、DVI、SAVI、MSAVI、EVI、RDVI 7个植被指数作为模型的自变量,叶面积指数(LAI)为因变量,用SPSS19.0统计软件和实测数据进行一元线性回归模型拟合,拟合结果如表4、图6所示。
由表4可知,所有7个模型的决定系数R2都超过了0.5,其中土壤调节植被指数(SAVI)与叶面积指数的一元线性回归模型拟合程度最优,决定系数R2为0.636 4;比值植被指数(RVI)的模型拟合程度也跟SAVI差距不大,R2为0. 636 2,这2个模型在7个模型中较优,与预期归一化植被指数(NDVI)可能会是最优模型的期望不一样;NDVI与叶面积指数的一元线性回归模型拟合程度属于中上,R2为0. 620 2;模型拟合程度最低的是差值植被指数(DVI),其R2为0.566 2。

表4 叶面积指数一元线性回归模型参数Table 4 The parameters of linear regression model

图6 SAVI与叶面积指数的一元线性回归模型Fig. 6 Linear regression model of SAVI and leaf area index
(2) 叶面积指数二次多项式回归模型
将 NDVI、RVI、DVI、SAVI、MSAVI、EVI、RDVI 7个植被指数作为模型的自变量,叶面积指数(LAI)为因变量,用SPSS19.0和实测数据进行二次多项式回归模型的拟合,拟合结果如表5、图7所示。

表5 叶面积指数二次多项式回归模型参数Table 5 The parameters of quadratic polynomial model

图7 RVI与叶面积指数的二次多项式回归模型Fig. 7 The quadratic polynomial model of RVI and leaf area index
由表5可知,所有7个模型的决定系数R2都超过了0.5,其中比值植被指数(RVI)与叶面积指数的二次多项式回归模型拟合程度最优,决定系数R2为0.657 9;增强型植被指数(EVI)的模型拟合程度排在第二,R2为0. 648 4,这2个模型在7个模型中较优;模型拟合程度最低的是差值植被指数(DVI),其R2为0.594 5。
(3)叶面积指数三次多项式回归模型
将 NDVI、RVI、DVI、SAVI、MSAVI、EVI、RDVI 7个植被指数作为模型的自变量,叶面积指数(LAI)为因变量,用SPSS19.0和实测数据进行二次多项式回归模型拟合,拟合结果如表6、图8所示。
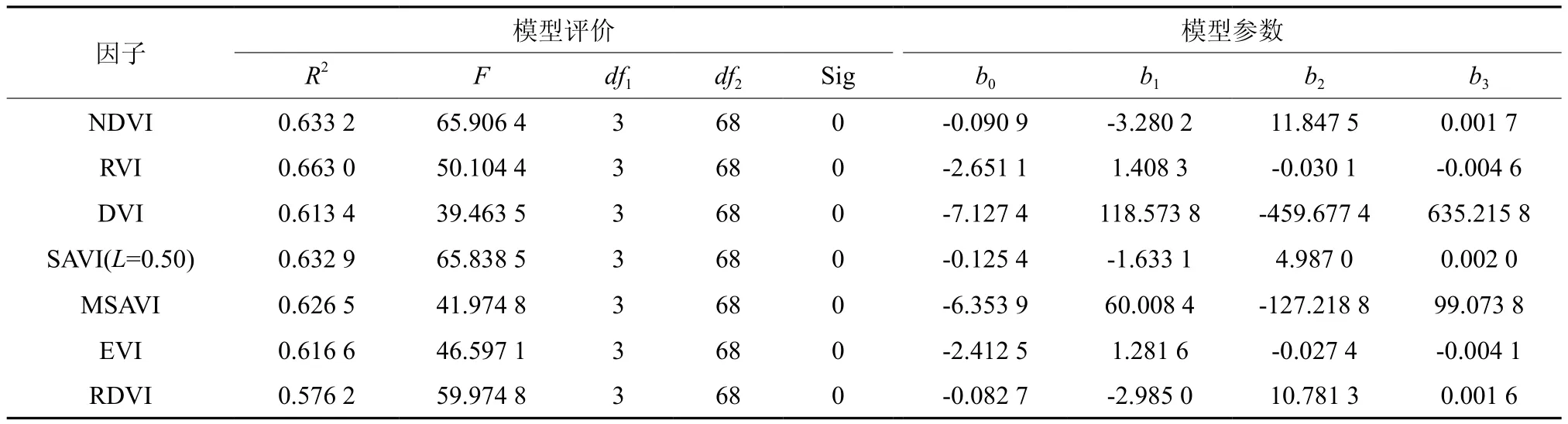
表6 叶面积指数三次多项式回归模型参数Table 6 The parameters of cubic polynomial model
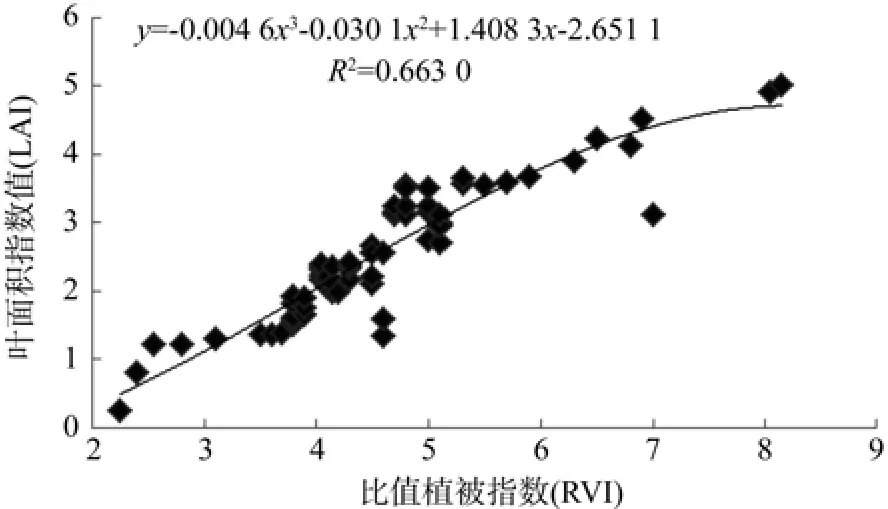
图8 RVI与叶面积指数的三次多项式回归模型Fig. 8 The cubic polynomial model of RVI and leaf area index
由表6可知,在7个模型的决定系数R2中最高的为比值植被指数(RVI),达到0.663 0,(RVI)与叶面积指数的三次多项式回归模型拟合程度最优;归一化植被指数(NDVI)的模型拟合程度排在第二,R2为0. 633 2,这2个模型在7个模型中较优的;模型拟合程度最低的是重归一化植被指数(RDVI),其R2为0.576 2。
(4)叶面积指数的指数回归模型
将 NDVI、RVI、DVI、SAVI、MSAVI、EVI、RDVI 7个植被指数作为模型的自变量,叶面积指数(LAI)为因变量,用SPSS19.0和实测数据进行指数回归模型拟合,拟合结果如表7、图9所示。

表7 叶面积指数指数回归模型参数Table 7 The parameters of exponential regression model
由表7可知,叶面积指数指数回归模型是所有拟合的回归模型中决定系数R2变化最大的一组,变化区间为0.482 9~0.707 6;其中R2最高的是叶面积指数与归一化植被指数(NDVI)拟合的模型,达到0.707 6;其次为土壤调节植被指数(SAVI),R2为0.662 4;模型拟合程度最低的是差值植被指数(DVI),其R2为0.482 9。
(5)叶面积指数对数回归模型
将 NDVI、RVI、DVI、SAVI、MSAVI、EVI、RDVI 7个植被指数作为模型的自变量,叶面积指数(LAI)为因变量,用SPSS19.0和实测数据进行对数回归模型拟合,拟合结果如表8、图10所示。

图9 NDVI与叶面积指数的指数回归模型Fig.9 The exponential regression model of NDVI and leaf area index
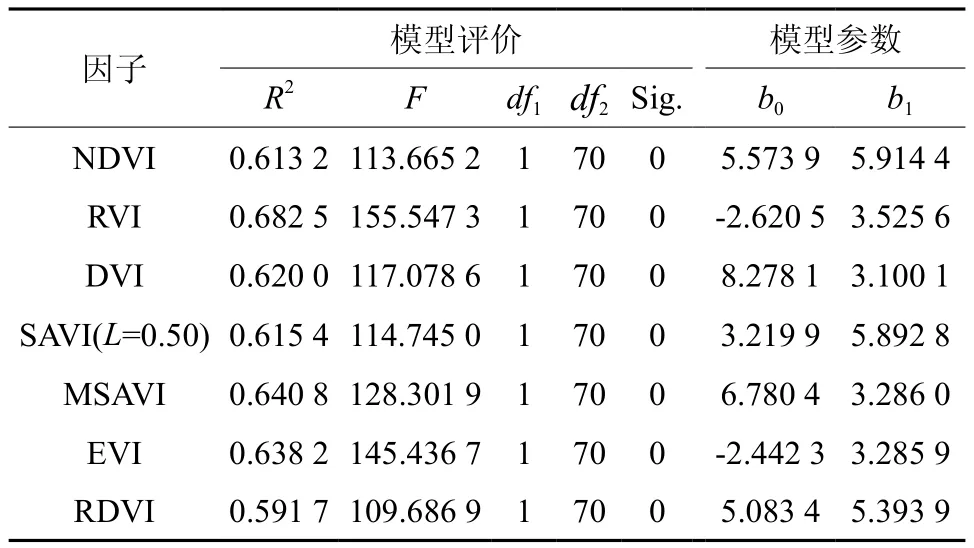
表8 叶面积指数对数回归模型参数Table 8 The parameters of logarithmic regression model

图10 RVI与叶面积指数的对数回归模型Fig. 10 The logarithmic regression model of RVI and leaf area index
由表8可知,在7个模型的决定系数R2中最高的为比值植被指数(RVI),达到0.682 5,RVI与叶面积指数的对数回归模型拟合程度最优;修正的土壤调节植被指数(MSAVI)的模型拟合程度排在第二,R2为0. 640 8,这2个模型在7个模型中较优;模型拟合程度最低的是重归一化植被指数(RDVI),其R2为0.591 7。
(6)叶面积指数幂函数回归模型
将 NDVI、RVI、DVI、SAVI、MSAVI、EVI、RDVI 7个植被指数作为模型的自变量,叶面积指数(LAI)为因变量,用SPSS19.0和实测数据进行幂函数回归模型的拟合,拟合结果如表9、图11所示。

表9 叶面积指数幂函数回归模型参数Table 9 The parameters of power function regression model
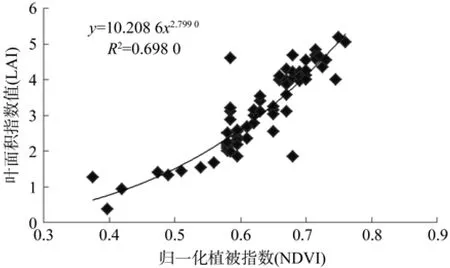
图11 NDVI与叶面积指数的幂函数回归模型Fig. 11 The power function regression model of NDVI and leaf area index
由表9可知,在7个模型的决定系数R2中最高的为归一化植被指数(NDVI),达到0. 698 0,NDVI与叶面积指数的幂函数回归模型拟合程度最优;土壤调节植被指数(SAVI)的模型拟合程度排在第二,R2为0.692 70,这2个模型在7个模型中较优;模型拟合程度最低的是差值植被指数(DVI),其R2为0.550 8。
4 叶面积指数回归模型精度检验
采用参数检验法和23组检验样本分别对6种叶面积指数回归模型拟合程度最高的估测模型进行参数检验,以此确定模型的精度,检验结果如表10所示。
将LAI实测值与各模型的LAI估测值进行一元线性回归模型拟合,分析拟合后的精度验证情况,结果如图12所示。
结合表10和图12可知,以NDVI为模型变量的指数估测模型与实测值的一元线性回归拟合方程可靠性高于其它,其估测模型的R2为0.809 7,均方根误差为0.689 8,平均相对误差为25.66%,即模型的总体估算精度为74.34%,为6个模型中误差最小;以SAVI为模型变量的一元线性回归模型R2为0.763 9,均方根误差为0.704 4,平均相对误差为26.79%,即模型的总体估测精度达到73.21%,误差精度排在第二;以RVI为模型变量的二次多项式估测模型的可靠性为6个模型最低,R2最小,为0.526 2,均方根误差为0.699 2,模型的平均相对误差为27.67%,即模型的总体估测精度为72.33%;以NDVI为模型变量的幂函数估测模型得到的LAI估测值总体精度是最低的,其平均相对误差为28.55%,即模型最终的估测总体精度为71.45%,R2为 0.668 4,均方根误差为0.742 0。分析可得,本研究建立的叶面积指数(LAI)估测模型总体精度都超过了70%,其中以NDVI为模型变量的指数模型的估测精度最高,达到了74.34%,模型为y=0.121 1exp(5.036x),可靠性也最高,可以很好地进行叶面积指数的估测,结果如图13所示。

表10 模型精度检验结果比较Table 10 The results of models test accuracy

图12 6个模型的估测值与LAI实测值与的精度验证Fig.12 The accuracy veri fi cation of LAI models estimated value and measured values
5 结论与讨论
本研究以Worldview-2遥感影像作为数据源,对东洞庭湖湿地核心区域进行了LAI估算研究,首先对典型的植被指数与叶面积指数(VI-LAI)的相关性进行了分析,然后选择了归一化植被指数(NDVI)、比值植被指数(RVI)、差值植被指数(DVI)、土壤调节植被指数(SAVI)、修正的土壤调节植被指数(MSAVI)、增强型植被指数(EVI)、重归一化植被指数(RDVI)7个植被指数作为VI-LAI的模型因子,这7个因子与LAI之间存在显著的相关性,相关系数达到0.73以上,最高为0.821 7,结果表明选取的因子对LAI有很密切的相关性,具有准确表达LAI特征的可行性。然后采用多种回归模型(包括一元线性、二次多项式、三次多项式、指数模型、对数模型、幂函数模型)与LAI实测数据进行拟合分析,选取出这6种回归模型的最优因子,然后利用实测数据作为检验样本,最终确立了以NDVI为模型变量的指数模型是用于LAI估测的最优模型,精度达到了74.34%。因此,本文中采用多植被指数比较建立的湿地植被VI-LAI反演模型可以比较准确获取湿地区域叶面积指数特征。但在研究中,也存在需要进一步完善的内容,本研究采用的是基于多植被指数比较的VI-LAI模型拟合,样本量还是比较有限,且未进行叶面积指数机理方面的研究比较,对基于物理模型的叶面积指数反演技术需要进行进一步研究,比较经验模型和机理模型在方法和尺度上的差异和适用性,得到更为准确的LAI估算结果。

图13 基于NDVI-LAI的指数估测模型的叶面积指数结果Fig.13 The results of leaf area index based on NDVI-LAI estimation model
[1]武红敢,乔彦友,陈林洪,等.马尾松林叶面积指数动态变化的遥感监测研究[J].植物生态学报,1997,21(5):485-488.
[2]席建超,张红旗,张志强.应用遥感数据反演针叶林有效叶面积指数[J].北京林业大学学报,2004,26(6):36-39.
[3]夏学齐,田庆久,杜凤兰.遥感提取叶面积指数的地形影响分析[J].遥感信息,2004,(2):16-19.
[4]骆知萌,田庆久,惠凤鸣.用遥感的方法计算森林LAI[J].南京大学学报,2005,41(3):253-258.
[5]浦瑞良,宫 鹏,John R Miller.美国西部黄松叶面积指数与高光谱分辨率CASE数据的相关分析[J].环境遥感,1993, 8(2):112-125.
[6]许章华,刘 健,龚从宏,等.马尾松毛虫寄主有效叶面积指数遥感反演模型研究[J].中南林业科技大学学报, 2012,32(10): 72-78.
[7]许全芝,张万昌.黑河流域叶面积指数的遥感反演[J].干旱区研究,2003,20(4):281-285.
[8]Ruiliang Pu, Peng Gong, Greg S Biging,et al.Extraction of Red Edge Optical Parameters From Hyperion Data for Estimation of Forest Leaf Area Index[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(4): 916-921.
[9]郭素娟,熊 欢,邹 锋,等,冠层分析仪在板栗冠层光辐射特征研究中的应用[J].中南林业科技大学学报,2013,33(6):12-16.
[10]Martin Schlerf,Clement Atzberger,Michael Vohland. Derivation of forest leaf area index from multispectral and hyperspectral remote sensing data[J].EAR Sele Proeeedings,2004,3(3):405-413.
[11]Martin Schlerf,Clement Atzberger,Joachim Hill. Remote sensing of forest biophysical variables using Hymap Imaging Spectrometer data[J].Remote Sensing of Environment, 2005,95(2): 117-194.
[12]Sandmeier. Sensitivity Analysis and Quality Assessment of Laboratory BRDF Data[J].Remote Sensing Environment, 1998,64(4): 176-191.
Research on remote sensing estimation of wetland vegetation LAI based on vegetation index comparation
LING Cheng-xing1, JU Hong-bo1, ZHANG Huai-qing1, SUN Hua2
(1. Institute of Forest Resource Information Techniques, CAF, Beijing 100091, China; 2. Research Center of Forestry Remote Sensing &Information Engineering, Central South University of Forestry & Technology, Changsha 410004, Hunan, China)
The research selects core area in wetland nature reserve of Dongting Lake in Hunan province as reserch object. In order to estimate the vegetation leaf area index(LAI) of core wetland region of Dongting Lake, high resolution image WORLDVIEW-2 data is utilzied to precisely leaf area index information. Then, Correlation between vegetation index and VI-LAI is analyzed. Seven vegetation indexes such as NDVI, RVI, DVI, SAVI, MSAVI, EVI and RDVI are selected as model factors of VI-LAI. Then multiple regression models (including unitary linear, quadratic polynomical, cubic polynomical, index model, logarithmic model and power function model)are adopted to take fi tting analysis with measrued LAI data to select optimal factors of the six regression models. After that, 23 groups of measured data are used as test samples to fi nally determine that the the index model with NDVI as model variable is the optimal model for LAI estimation, Which makes the pricesion up to 74.34%.The experimental result shows that Vegetation Index Comparation mothod is an effective sway in wetland remote sensing leaf area index(LAI)Estimation.
wetland;worldview-2 image;vegetation index; leaf area index(LAI)estimation
S771.8
A
1673-923X(2016)05-0011-08
10.14067/j.cnki.1673-923x.2016.05.003
2015-05-10
国家重大专项(21-Y30B05-9001-13/15-2);国家高技术研究发展计划(863计划)(2012AA102001)
凌成星,博士研究生 通讯作者:张怀清,研究员;E-mail:zhang@caf.ac.cn
凌成星,鞠洪波,张怀清,等. 基于植被指数比较的湿地区域LAI遥感估算研究[J].中南林业科技大学学报,2016, 36(5):11-18.
[本文编校:谢荣秀]

