抗野值卡尔曼滤波在火箭弹落点估计中的应用*

闫小龙,陈国光,杨 东

(1 中北大学,太原 030051;2 豫西工业集团有限公司,河南南阳 473000)



抗野值卡尔曼滤波在火箭弹落点估计中的应用*

闫小龙1,陈国光1,杨 东2

(1 中北大学,太原 030051;2 豫西工业集团有限公司,河南南阳 473000)

为了实现火箭弹精确打击,根据飞行弹道参数对弹道进行修正。应用文中提出的双气动参数辨识算法,去除出现在信号初始阶段的野值,降低对后续卡尔曼滤波的影响。随后利用基于新息判断野值的卡尔曼滤波器,结合质点弹道模型,建立了卡尔曼滤波弹道模型,对一段飞行参数进行野值的去除与滤波,并对火箭弹落点进行外推。结果表明,该方法可以将量测数据中的野值有效去除。落点估计可知,外推时间的推后可以增加预估的精度。

火箭弹弹道修正;卡尔曼滤波;双气动参数辨识;野值;落点估计

0 引言

随着对火箭弹的射击精度要求的不断提高,修正火箭弹逐步被广泛的应用。其工作原理是根据火箭弹的飞行观测数据(如雷达数据、GPS数据等)对火箭弹飞行状态进行最优估计并预测落点,并将预测落点与拟击中目标进行比较,计算出偏差,根据偏差的大小对火箭弹进行修正。

文中针对使用三坐标雷达对火箭弹飞行轨迹观测,在观测过程中由于雷达探测有较大的误差,就使得在对火箭弹进行落点估计时使用的数据有较大的影响。这就要求对弹道数据进行滤波,滤除雷达信号中的随机噪声。但是在雷达实际探测中不但会有随机噪声,而且还会有较少但是与实际数值偏差较大的噪声,这些偏差较大的噪声称为“野值”,在滤波过程中这些野值会对滤波算法有较大的影响,严重影响处理结果精度。在此前提条件下文中提出一种带有野值剔除的卡尔曼滤波算法,提高了对火箭弹落点估计的准确度[1]。

1 火箭弹外弹道滤波、外推模型

在得到雷达量测数据后,要根据弹道模型对实测弹道进行滤波处理,并外推落点[2],之后及时的反馈偏差数据,随之火箭弹的执行机构进行弹道修正。由于修正火箭弹需要及时的解算进行落点估计,所以在同时要求解算速度与解算精度的前提下,选择计算速度较快的质点弹道模型。

(1)

取x1、x2、x3、x4、x5、x6作为卡尔曼滤波的状态变量,即(x1,x2,x3,x4,x5,x6)T=(vx,vy,vz,x,y,z)T。则有系统状态方程:

(2)

式中W(k)是均值为零的随机噪声。

2 滤波量测方程

三坐标雷达的测量值,即斜距r,方位角β和高低角ε。可得雷达测量值与地面坐标系的关系:

(3)

式中,(x0,y0,z0)为雷达天线中心在地面坐标系中的坐标。

坐标雷达的测量阵列为Z=[r,β,ε]。Vk为雷达测量噪声,假定为零均值的高斯白噪声,则离散形式的量测噪声方差矩阵为:

(4)

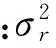
在火箭弹发射过程中,雷达坐标系并不正好处于炮位坐标系,则需要坐标系之间的转换,转换关系为:

式中：εx、εy、εz为三维空间直角坐标变换的3个旋转角,R1(εx)、R2(εy)、R3(εz)分别为与它相对应的旋转矩阵。

则可得量测方程为:

(6)

3 卡尔曼滤波

卡尔曼滤波方程组分为两大部分,第一部分为卡尔曼滤波方程,这一部分负责向前推算轨迹状态;第二部分为卡尔曼滤波器的增益矩阵递推算式,这一部分用于反馈先验估计,并对预测进行修正。离散系统的卡尔曼最优估计基本公式为[3]:

最优预测估计方程:

(7)

最优滤波估计方程:

(8)

最优滤波增益矩阵方程:

K(k)=P(k|k-1)HT(k)·

[H(k)P(k|k-1)HT(k)+Rk]-1

(9)

最优预测估计误差方差阵方程:

P(k|k-1)=Φ[k,k-1]P(k-1|k-1)·

ΦT(k,k-1)+Γ(k|k-1)Qk-1ΓT(k|k-1)

(10)

最优滤波估计误差方差阵方程:

P(k|k)=K(k)RkKT(k)+

[I-K(k)H(k)]P(k|k-1)[I-K(k)H(k)]T

(11)

t0时刻的状态向量X(0)的统计特性E{X(0)}及P(0)都已知道,那么,为了得到无偏估计,应取值:

4 野值的判别与处理

由于在实际情况中,量测信号要经过传输系统、数据采集转换系统等环节,才能把数字形式的目标信号送卡尔曼滤波,这样不但会带有大量的随机噪声,而且有可能受到外界无规律的干扰而产生一些与真实数据相差较大的野值,这些野值的存在使得在进行卡尔曼滤波时对滤波结果有较大的影响[4]。

令:

(12)

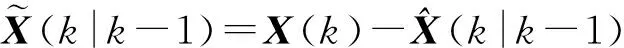
H(k)P(k|k-1)HT(k)+R(k)

(13)

(14)

根据式(14)对此n点进行抛物线拟合,并计算残差δ1～δn。

当δi>C时,认为该点为野值点,并去除;

当δi

5 计算仿真

为了检验该滤波器的实际滤波效果,需要对其进行数值仿真计算。文中以某型火箭弹为例进行仿真,采用5D弹道模型计算生成弹道数据,然后加入均值为零的高斯白噪声引入雷达噪声,加入不定周期的较大误差作为引入的雷达测量野值,形成三坐标雷达量测数据[5]。用带野值处理卡尔曼滤波器对雷达测得的数据进行野值的判别、处理、滤波,并用质点外弹道方程外推弹道,预估落点(x,z),模拟弹丸发射2.5 s后雷达开始跟踪量测目标,采样间隔为0.1 s。在模拟雷达量测数据至40 s左右,开始对弹道数据进行滤波处理,持续监控20 s左右至60 s时停止滤波处理。图1～图3为野值去除以及滤波处理结果。

图4为带去野值功能的卡尔曼滤波后原数据的差,结果表明滤波后的差值收敛很快,经过20 s后趋于稳定。图5为不带去野值功能的卡尔曼滤波后原数据的差,结果表明滤波后的差值在经过40 s后才趋于稳定,且差值较有去野值功能的卡尔曼滤波要大很多。当野值去除以及滤波工作结束后取60 s时的滤波数据结果,并输入质点弹道方程对火箭弹落点(x,z)进行估计。并最终与生成的弹道进行对比,得出落点估计的差值。图6为x方向上预估落点与原弹道差值,图7为z方向上预估落点与原弹道差值。

图1 x方向数据处理

图2 y方向数据处理

图3 z方向上的数据处理

图4 去野值滤波坐标轴方向上的滤波后原数据差

图8为外推弹道落点坐标误差与外推开始距击中目标时长的关系,由图可以看出随着外推时间的不断提前,其外推的精准度逐步降低。但是在提前到一定的时间后,精度降低的速度逐步放缓而趋于稳定。因此合适的选取外推开始时间可以有效的增加落点预测的精度,但是一再的推迟外推时间,降低了落点估计的意义。

图5 不去野值滤波坐标轴方向上的滤波后原数据差

图6 x轴外推落点与原弹道差

图7 z轴外推落点与原弹道差

图8 外推开始时刻距落地时刻的时长与落点估计精度的关系

6 总结

文中针对三坐标雷达量测的火箭弹弹道数据,通过可以去除量测数据中野值的卡尔曼滤波器滤除雷达测量信号中的随机噪声,根据滤波结束时的弹道数据输入外推质点弹道方程,得到估计落点,为火箭弹的修正提供了有效数据。用生成弹道数据进行数据仿真结果表明,在有野值存在且雷达的随机噪声幅值很大的情况下,经过该滤波器滤波后可以获得较为接近真实值的弹道数据。在外推过程中,随着外推时间的不断推后,外推的精度会不断的提高。

[1] 俞济祥. 卡尔曼滤波及其在惯性导航中的应用 [M]. 北京: 航空专业教材编审组, 1984: 101-102.

[2] 王志贤. 最优状态估计与系统辨识 [M]. 西安: 西北工业大学出版社, 2004: 76.

[3] 高宁, 周跃庆, 杨晔, 等. 抗野值自适应卡尔曼滤波方法的研究 [J]. 中国惯性技术学报, 2003, 11(3): 25-28.

[4] 张远, 陈勇, 吴昊. 弹道导弹落点预报方法研究 [J]. 导弹与航天运载技术, 2014(3): 5-10.

[5] 李广军, 李忠, 崔继仁. 新型抗野值的Kalman滤波器研究 [J]. 计算机应用与软件, 2013, 30(1): 136-138.

Application of Kalman Filter Restraining Outliers in Estimation of Rockets Impact Point

YAN Xiaolong1,CHEN Guoguang1,YANG Dong2

(1 North University of China, Taiyuan 030051, China; 2 Yuxi Industries Group Co. Ltd, Henan Nanyang 473000, China)

Precise rocket strike, requires trajectory correction according to trajectory parameters. In this paper, double aerodynamic parameter identification algorithm was used to remove appears in initial phase of signal outliers, reduce impact on subsequent Kalman filter. Intermediate outlier measurement information was used to judge based on prediction error of the Kalman filter combined with particle trajectory model for construction of the Kalman filter trajectory model. The Kalman filter trajectory model was used to remove and filter outliers of a section of flight parameters, and extrapolate the rockets impact point. The simulation results show that, the filter can remove and filter the outliers in radar measurement data effectively. We can know that prediction accuracy can increase by postponing extrapolation.

rocket trajectory correction; Kalman filter; double aerodynamic parameter identification; outliers; impact point estimation

2015-05-13

闫小龙(1988-),男,山西太原人,硕士研究生,研究方向:智能弹药。

TJ765

A