“平面图形的认识(二)”重难点突破
徐仙
“平面图形的认识(二)”重难点突破
徐仙
本章是“平面图形的认识(一)”的延续和提高.下面为同学们解读本章学习中的几个难点.
难点一:“三线八角”中的识角
两条直线被第三条直线所截,图形中共有八个小于180°的角,我们把这个图形称为“三线八角”图,其中没有公共顶点的两个角可以分为三类:同位角、内错角、同旁内角,它们是进一步学习平行线的判定和性质的基础.同位角:分别在两条直线的同一侧,并且都在第三条直线的同一旁;内错角:在两条直线之间,并且分别在第三条直线的两旁;同旁内角:在两条直线之间,并且都在第三条直线的同一旁.
识别的关键:是在各种图形中准确地辨别出没有公共顶点的两角是由哪两条直线被哪一条直线所截构成的,即通过两角如何找准“三线”,找“三线”的难点是找准“截线”.
例1如图1,按图中角的位置,判断正确的是().
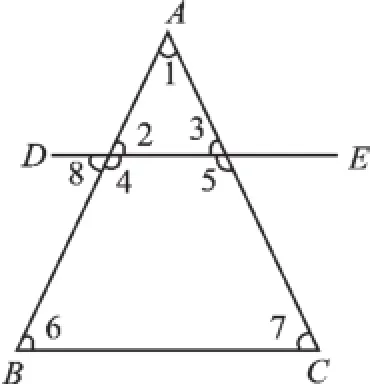
图1
A.∠1与∠2是同位角
B.∠1与∠4是内错角
C.∠5与∠7是同旁内角
D.∠4与∠8是同位角
【分析】首先要辨别出没有公共顶点的两角是由哪两条直线被哪一条直线所截构成的,再对照定义进行判别.
【答案】C.
【点评】在“三线八角”识角中,关键要找到截线与被截直线,再对照同位角、内错角、同旁内角定义进行判别.技巧:将已知的没有公共顶点的两角的两边用铅笔重描一下,显现出形成两角的直线,既可以看出这两角是否属于“三线八角”中的同位角、内错角、同旁内角,也可以看出是由哪两条直线被哪一条直线所截.
难点二:平行线判定与性质的运用
平行线的判定:同位角相等两直线平行;内错角相等两直线平行;同旁内角互补两直线平行.平行线的性质:两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.平行线的“判定”和“性质”既紧密联系又有根本区别,往往容易混淆,学习时应注意以下几点.1.分清因果关系.平行线的“判定”是由角的相等或互补推出两直线平行,角相等或互补是前提,是因,两直线平行是结论,是果;平行线的“性质”是由两直线的平行推出角相等或互补,两直线平行是前提,是因,角相等或互补是结论,是果.
例2已知如图2,∠1+∠2=180°,∠A=∠C,AD平分∠BDF,求证:BC平分∠DBE.
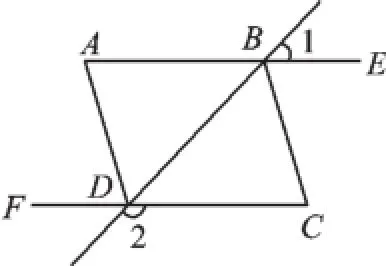
图2
【分析】只要求得∠EBC=∠CBD,由∠1+∠2=180°推出∠1=∠BDC,从而推出AE∥FC,从而推出∠C=∠EBC,而∠A=∠C,从而可得AD∥BC,最后再运用平行线的性质和已知条件便可推出∠EBC=∠DBC.
证明:∵∠BDC+∠2=180°(平角定义)
又∵∠1+∠2=180°(已知)
∴∠1=∠BDC(同角的补角相等)
∴AE∥FC(同位角相等,两直线平行)
∴∠C=∠EBC(两直线平行,内错角相等)
又∵∠A=∠C(已知)
∴∠A=∠EBC(等量代换)
∴AD∥BC(同位角相等,两直线平行)
∴∠ADB=∠CBD(两直线平行,内错角相等)
∠ADF=∠C(两直线平行,同位角相等)
又∵AD平分∠BDF(已知)
∴∠ADB=∠ADF(角平分线的定义)
∴∠EBC=∠DBC(等量代换)
∴BC平分∠DBE(角平分线的定义)
【点评】本题反复应用平行线的判定与性质,见到“平行”应想到有关的角相等,见到有关的角相等,就应想到能否判断直线间的平行关系.把平行线的判定与性质紧密结合在一起也就是将直线平行与角相等联系在一起.这样解题得心应手,灵活自如.
难点三:钝角三角形高的作法
三角形的高:从三角形的一个顶点向它的对边所在直线作垂线,顶点与垂足之间的线段叫作三角形的高.
例3△ABC中,∠A>90°,图3为某同学作的AC边上的高AD,是否正确?为什么?若不正确,请你作出符合条件的高.
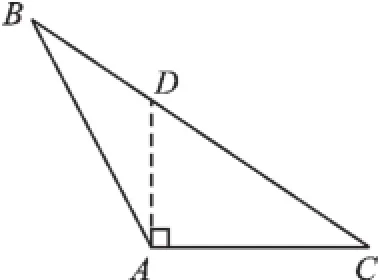
图3
【分析】AC边上的高应由AC所对的顶点B向AC边所在的直线作垂线,而不是只保证垂直AC就可以.
解:此作图不正确,因为AC边上的高应由AC所对的顶点B向AC边所在的直线作垂线,而不是过点A作,符合条件的高应为下图中线段BE.
【点评】正确理解三角形高的定义是作三角形高的关键.
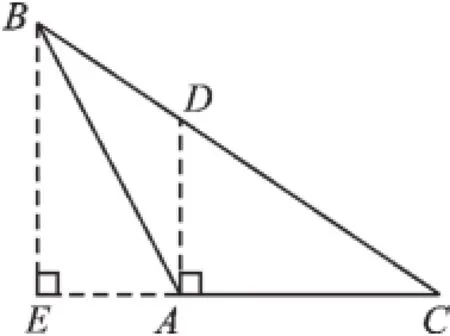
图4
难点四:三角形确定第三边的取值范围
“三角形两边的和大于第三边”是这章中的重要定理,从这个定理出发还可以得出一些有用的结论,这些结论在实际生活中可以起到很大的作用.
例4已知△ABC的两边AC=5,BC=8,求第三边AB的取值范围.
【分析】我们可以从动态的角度来看待这个问题,让BC不动,而AC绕C点旋转.我们发现当AC与BC在同一条直线上时AB有最大值,但由于AB是△ABC的一边,故AB<AC+BC;当AC与BC重合时,AB有最小值,故AB>BC-AC.
解:∵BC+AC=13,BC-AC=3,
∴3<AB<13.
【点评】“三角形两边的和大于第三边”和由此得出的“三角形两边的差小于第三边”,都是由“两点之间线段最短”这个定理得出的.在已知三角形两边长求第三边范围时,不仅要考虑“两边的和大于第三边”,同时也要确保“两边的差小于第三边”.
(作者单位:江苏省丹阳市华南实验学校)

