带裂缝钢筋混凝土梁有限元分析

淦 家 超

(武汉理工大学土木与建筑学院，湖北 武汉 430070)



带裂缝钢筋混凝土梁有限元分析

淦 家 超

(武汉理工大学土木与建筑学院，湖北 武汉 430070)

通过有限元软件ANSYS，模拟了钢筋混凝土梁从开裂到破坏的全过程，并从裂缝位置、宽度及深度等方面，分析了裂缝对钢筋混凝土梁的影响，得到一些有价值的结论，为钢筋混凝土裂缝的治理奠定了基础。

钢筋混凝土，有限元模型，裂缝，挠度

1 概述

近几十年来随着计算机得到高速发展，非线性有限元理论和有限元软件也变得成熟完善。有限元软件作为非常厉害的数值分析软件已经在土木工程领域得到了广泛的运用。与钢筋混凝土试验比较起来，有限元软件建立模型模拟要更加简便、实用与节省经费。利用ANSYS有限元软件来模拟钢筋混凝土从开裂到破坏的全过程，来分析钢筋混凝土裂缝产生的过程与机理。

2 钢筋混凝土有限元模型

2.1 混凝土和钢筋单元的选择

在ANSYS一般都有Soild65单元用来模拟混凝土单元[1]。Soild65单元又被称作为3D加筋混凝土实体单元，它具有受拉开裂和受压破碎的力学性能。Soild65单元有8个节点，每个节点都有3个自由度(X，Y，Z三个方向的平动位移)，该单元可以定义3个方向的独立配筋。Soild65单元最为重要的是对材料的非线性的处理，它可用来模拟混凝土开裂、压碎、塑性变及徐变，还可以模拟钢筋的拉伸、压缩、塑性形变及蠕变，但不能模拟钢筋的剪切。

钢筋采用Link180单元来模拟，Link180又被称为3D有限元变杆单元，它在工程上具有广泛的应用，可以用来模拟桁架、缆索、连杆和弹簧等。该单元可以承受拉压但是不能够承受弯矩，该单元是由两个节点所组成，每个节点都有3个自由度(X，Y，Z三个方向的平动位移)，该单元具有塑性、蠕变、旋转、大变形等功能。

2.2 材料的本构关系

在有限元分析中钢筋可以采用双直线型模型，该模型的钢筋应力应变如图1所示，这种模型是不计屈服强度的上限和由于钢筋硬化导致钢筋应力的增加。OB段是弹性阶段，弹性段是一条以钢筋的弹性模量为斜率的直线。B点是钢筋屈服的下限，C点是钢筋应力强化的开始点。该模型的数学表达式如下[2]：

(1)

对于受弯的钢筋混凝土构件，混凝土的应力—应变关系曲线是最基本的本构关系。它是钢筋混凝土构件的截面刚度、承载力和延性、有限元分析的重要理论基础，是不可或缺的物理方程。混凝土单轴受压下的应力—应变关系(如图2所示)采用Hognestad在1951年提出的应力—应变全曲线方程。其数学表达式如下：

(2)

3 钢筋混凝土有限元实例分析

3.1 建立钢筋混凝土梁有限元模型

运用ANSYS软件对一根截面为矩形的钢筋混凝土梁进行有限元分析。建立两端简支的钢筋混凝土梁有限元模型，该钢筋混凝土梁的各参量：梁长4 m，跨度3.6 m；钢筋混凝土截面梁高为300 mm，宽度为150 mm；钢筋采用HRB335，受压钢筋直径为10 mm，受拉钢筋直径为20 mm，钢筋保护层厚度为30 mm。梁受到均布荷载q的作用，均布荷载q=25 kN/m。钢筋混凝土梁尺寸以及配筋如图3所示。

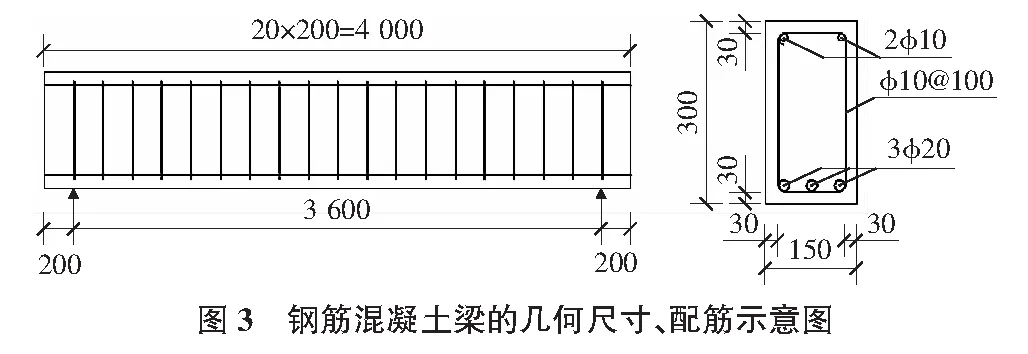
3.2 建立钢筋混凝土有限元模型

钢筋混凝土的三种有限元模型，通过对分离式、整体式、组合式这三种模型的比较发现，还是分离式建模方式与我们实际情况比较接近。所以本文采用分离式建模方式，混凝土单元采用Soild65单元，钢筋采用Link180单元，不考虑钢筋与混凝土的粘结[5]。钢筋和混凝土单元如图4所示。

3.3 裂缝对钢筋混凝土梁极限承载力的影响

1)设置裂缝位置及宽度。该钢筋混凝土梁的截面尺寸为300 mm×150 mm，其梁长4 m，跨度3.6 m。由于该钢筋混凝土简支梁具有对称性，只要在梁的左半端设置裂缝就行。裂缝的位置在距离钢筋混凝土梁左端0.5 m，1 m，2 m处。裂缝宽度要根据GB 50010—2010混凝土结构设计规范中裂缝等级控制以及最大裂缝要求。设置3种裂缝宽度分别为0.2 mm，0.25 mm，0.3 mm，而裂缝深度设置为6 mm，9 mm，15 mm，21 mm四种情况。这样总共会有36种裂缝状态下钢筋混凝土梁的变形情况[6,7]。具体操作如下所示：

首先将裂缝设置在距离钢筋混凝土梁左端0.5 m处，接着将裂缝的宽度设定为0.2 mm，再将裂缝的深度从6 mm到21 mm依次改变。运用ANSYS有限元软件对钢筋混凝土结构进行有限元分析，接着将钢筋混凝土梁跨中最大挠度依次记录下来。收集完后再将裂缝的宽度变成0.25 mm和0.3 mm，再将裂缝的深度从小到大依次改变。这样就收集到裂缝在0.5 m处钢筋混凝土跨中的最大挠度。

2)ANSYS计算结果分析。运用ANSYS软件运行钢筋混凝土梁的各种工况，将各种工况跨中节点位移和最大挠度的数据整理成表1。对于钢筋混凝土梁的结果可以从3个方面来研究：a.裂缝处于梁不同位置对钢筋混凝土梁变形的影响；b.不同的裂缝宽度对钢筋混凝土梁变形的影响；c.不同的裂缝深度对钢筋混凝土梁变形的影响。

表1 裂缝在0.5 m，1 m，2 m处跨中位移及最大挠度 cm

研究不同裂缝长度对钢筋混凝土梁变形的影响，用钢筋混凝土梁的最大挠度为纵坐标，不同的裂缝长度为横坐标。将表1各种工况的数据整理成图5，从图5中可以看出当裂缝在梁端位置和裂缝宽度确定后，这里以裂缝位置在距离梁端1 m处为例，当裂缝深度增加时，钢筋混凝土梁的跨中最大挠度值也在增加。早期挠度增加的比较缓慢，当裂缝达到15 mm时，挠度增加速度变快，呈现抛物线形状。当裂缝位置距离梁端0.5 m和2 m时情况是一样的，从这里可以看出，裂缝长度对钢筋混凝土梁的挠度变化影响是很大的。

研究不同位置的裂缝钢筋混凝土梁变形的影响，首先确定裂缝宽度为定值，接着用钢筋混凝土梁的最大挠度为纵坐标，不同裂缝位置作为横坐标。将表1各种裂缝宽度的工况的数据整理成图6。从图6可以看出，当裂缝宽度为0.2 mm时，裂缝的位置从梁的左端向跨中靠近过程中，钢筋混凝土的最大挠度逐渐增加；而且还可以看出当裂缝长度增加时，钢筋混凝土梁的最大挠度可增加的越多。当裂缝宽度增加到0.25 mm和0.3 mm时，同一裂缝长度的拟合曲线基本吻合，可以看出当裂缝宽度增加时，基本不影响钢筋混凝土梁的最大挠度。

研究不同裂缝宽度对钢筋混凝土梁变形的影响时，首先确定裂缝位置或者裂缝长度两个当中的一个。这里我们先确定裂缝位置在跨中时，裂缝宽度与钢筋混凝土梁最大挠度的关系。以钢筋混凝土梁的最大挠度为纵坐标，不同裂缝宽度作为横坐标。将表1各种工况的数据整理成图7。从图7可以看出，当裂缝位置距离梁端2 m时，裂缝宽度从0.2 mm增加到0.25 mm的过程中，钢筋混凝土的最大挠度变化基本不大；从图中还可以看出当裂缝长度增加时，钢筋混凝土梁的最大挠度增加了。当裂缝位置在0.5 m以及1 m处时情况跟上面情况一样，就不一一赘述。可以看出当裂缝宽度增加时，基本不影响钢筋混凝土梁的最大挠度。

4 结语

为了得到裂缝对钢筋混凝土梁的影响，利用ANSYS有限元软件对带裂缝的钢筋混凝土梁进行模拟分析。通过ANSYS对钢筋混凝土梁设置不同裂缝长度、裂缝宽度以及裂缝的位置，对钢筋混凝土梁的变形进行观察，从分析结果得到以下结论：

1)钢筋混凝土开裂后，通过改变钢筋混凝土梁裂缝宽度，发现其对钢筋混凝土梁最大挠度影响非常小，三种裂缝宽度最大挠度基本一致。

2)对于钢筋混凝土梁，当裂缝位置从梁端向跨中靠拢时，钢筋混凝土梁的最大挠度是逐渐增加的。裂缝位置会对钢筋混凝土梁产生影响。

3)裂缝长度的改变对钢筋混凝土梁最大挠度影响显著，而且钢筋混凝土梁最大挠度随着裂缝长度增加呈现抛物线关系。

[1] 郝文化.ANSYS土木工程应用实例[M].北京:中国水利水电出版社,2004.

[2] 余学芳.混凝土结构裂缝的有限元模拟[D].杭州:浙江大学博士学位论文，2012.

[3] 钟明全.部分预应力混凝土梁正截面钢筋应力及裂缝的试验研究[D].成都:西南交通大学土木工程学院,1985.

[4] Tepfers R.Fatigue of plain concrete subjected to stress reversals[J].ACI J,Special Publication,1982(25)：136-137.

[5] 林延杰,魏显峰,齐永顺.少筋混凝土结构断裂数值模拟[J].建筑施工,2007(16)：29-31.

[6] 刘茂军,赵艳林,吕海波.钢筋混凝土结构裂缝产生的机理分析及应对策略[J].混凝土,2009(29)：10-11.

[7] 顾祥林,许 勇,张伟平.钢筋混凝土梁开裂后刚度退化研究[J].结构工程师,2005(12)：38-39.

Finite element analysis of steel reinforced concrete beam with cracks

Gan Jiachao

(CollegeofCivil&Building,WuhanUniversityofTechnology,Wuhan430070,China)

Based on finite element software ANSYS, the paper simulates the whole process of steel reinforced concrete beam from cracking to damage, analyzes impacts of cracks upon steel reinforced concrete beam from aspects of cracks location, width and depth, and finally draws some valuable conclusions, which has laid a foundation for steel reinforced concrete cracks treatment.

steel reinforced concrete, finite element model, cracks, deflection

1009-6825(2016)32-0056-03

2016-09-06

淦家超(1991- )，男，在读硕士

TU375.1

A