含结构面岩体试样单轴强度与变形特征*

郭松峰 祁生文 李星星 邹 宇 张世殊

GUO Songfeng① QI Shengwen① LI Xingxing① ZOU Yu① ZHANG Shishu②



含结构面岩体试样单轴强度与变形特征*

郭松峰①祁生文①李星星①邹 宇①张世殊②

结构面是岩体区别于岩石材料的一大特征，其产状、迹长、密度等参数对岩体的力学性质有着重要影响。本文利用FLAC3D对含结构面岩体试样的单轴压缩特性进行了较为系统的数值模拟研究。文中建立了含不同组贯通性结构面的岩体试样模型和含不同倾角及迹长的非贯通结构面岩体试样模型，对每个试样进行单轴压缩试验的数值模拟，结构体和结构面均采用Mohr-Coulomb剪切和拉伸破坏准则。模拟中用编制的伺服控制程序通过调节加载速度，控制试样内最大不平衡力，研究含结构面试样单轴压缩情况下的变形、强度及破坏方式等特征。模拟结果显示，含1-3组贯通性结构面试样呈现各向异性特征，而含4组贯通性结构面试件呈现各向同性特征。随着贯通性结构面数量的增多，同尺寸试件的变形强度参数劣化。含单组非贯通性结构面试件，其单轴压缩模拟试验的应力-应变曲线峰值后出现应力降。基于Mohr-Coulomb抗剪强度准则和损伤理论所得的解析解与数值模拟结果所得的非贯通性结构面试件的单轴压缩强度不符，说明用抗剪强度准则与损伤理论刻画非贯通结构面试样的强度并不合理。随着非贯通性结构面贯通率的增大，试件的变形、强度参数劣化。含单组结构面试件的破坏方式可分为结构面控制破坏，结构面部分控制破坏和结构面不控制破坏3种类型，而随着结构面组数的增多，结构面控制试样破坏的概率增加。

岩体 强度 变形 单轴 结构面

GUO Songfeng①QI Shengwen①LI Xingxing①ZOU Yu①ZHANG Shishu②

0 引 言

对含结构面岩体的强度、变形特性的研究，从上个世纪初以来已有不少国内外学者进行了不懈的努力，并取得了诸多成果。早在1960年，Jaeger(1960)就基于Mohr-Coulomb准则提出了含单条(组)贯通性结构面试样的强度解析解(图1)，岩体最小抗压强度σ1min为结构面抗剪强度，岩体破坏形式为沿结构面滑动破坏，此时结构面方向与最大主应力方向夹角β为45°-1/2φw； 岩体最大抗压强度σ1max为岩块抗剪断强度，岩体破坏形式为岩块剪断破坏，破裂面方向与最大主应力夹角β为45°-1/2φ； 当β1≤β≤β2时，介于沿结构面破坏的最低强度与岩块剪断破坏之间的破坏压应力见式(1)～式(3)。

(1)

(2)

(3)

式中，φw、cw分别为结构面内摩擦角、黏聚力； φ、c分别为岩块的内摩擦角、黏聚力； β1、 β2为两临界值，见图1b所示。

如果岩体含多组贯通结构面，岩体强度的确定方法是分步运用单结构面理论即， 式(1)～式(3)，分别绘出每一组结构面单独存在时的强度包络线和应力莫尔圆，岩体总沿着强度最小的那组结构面破坏，岩体强度为此组结构面强度(Sun， 1988； Hudson et al.，2000； Cai et al.，2009)，图1d。Halakatevakis et al.(2010)将Barton-Bandis结构面破坏判据代替Mohr-Coulomb准则对结构面岩体强度理论进行理论探索。但是，以上解析解均未考虑多结构面情况下结构面之间的相互作用，而这种作用在现实中是不可忽视的。Hoek与Brown等人通过大量岩石试验和现场监测提出了著名的Hoek-Brown经验强度准则，但是该准则未考虑岩体的各向异性(Hoek et al.，1980； Hoek， 1986)。

室内岩石力学试验方面，国内外很多学者都进行了大量的研究。对含一组结构面岩体试样，Müller et al.(1965)，Pomeroy et al.(1971)，Nasseri et al.(2003)进行了常规三轴试验研究，得出了含一组贯通性结构面试件的各向异性特征，随着围压的升高其各向异性逐渐向各向同性转化，并拟合出了Mohr-Coulomb准则的指数形式； 向天兵等(2009)则进行了真三轴试验研究，对单条贯通性结构面试件破坏机制进行了探索； Bobet et al.(1998)，Wong et al.(2009)对含埋藏型结构面试样进行了单轴试验研究，观察了裂纹的扩展和拼接现象。对两条以上结构面的试样，John(1969)，Ladanyi et al.(1972)，Einstein et al.(1970)进行了一些试验研究，但是总体来说，含结构面试样复杂的制作技术限制了室内大量系统的试验研究。

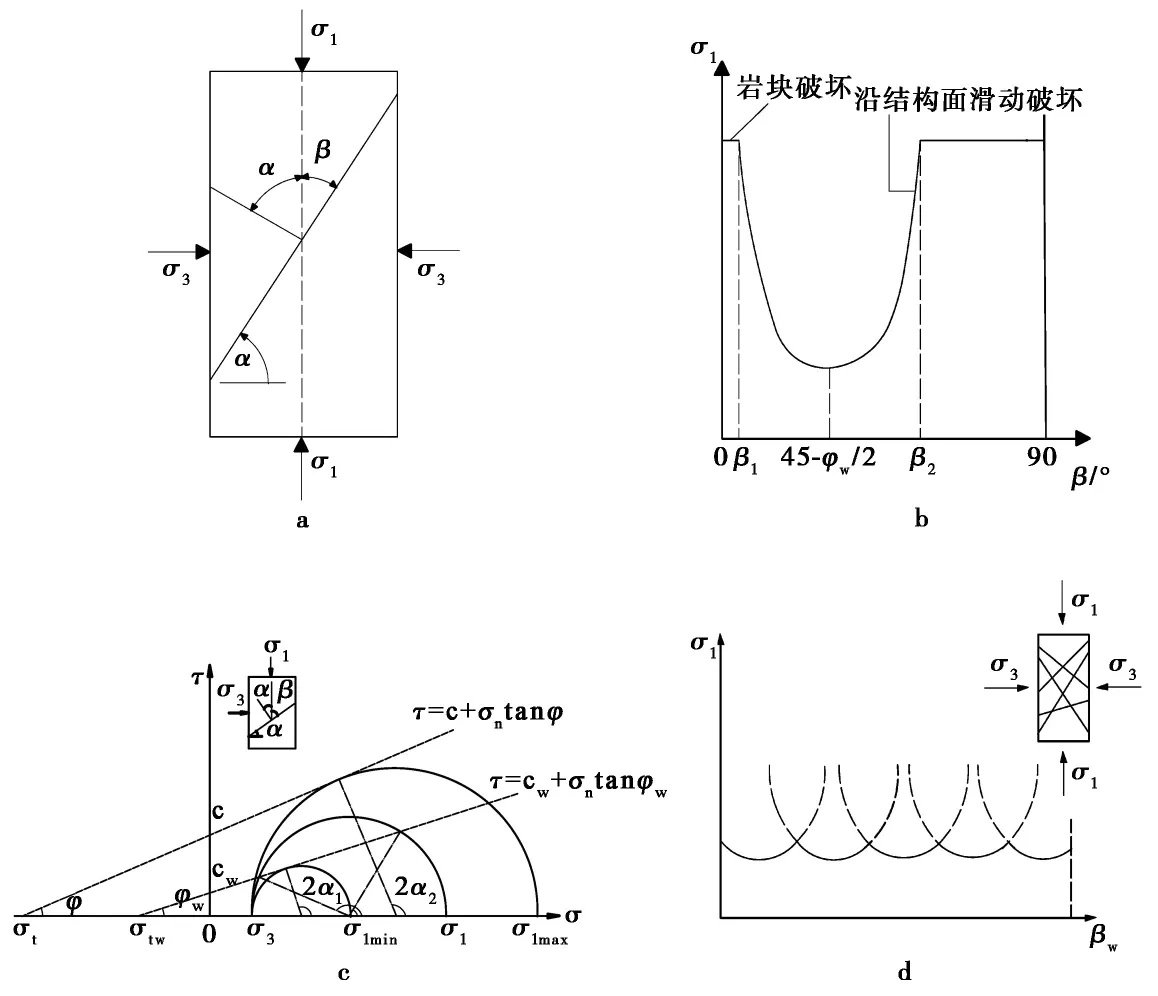
图1 含贯通结构面试件抗压强度解析解示意图(Jaeger, 1960)

随着计算机模拟技术在岩体力学中的应用，国内外学者对含结构面试样的强度、结构也进行了大量的模拟试验研究。Vasarhelyi et al.(2000)基于DDM模拟了单轴压缩情况下试样中埋藏型节理的扩展和连通，Halakatevakis et al.(2010)利用UDEC模拟了1组到3组结构面的抗压强度，晏长根等(2009)利用FLAC3D对节理岩体的变形强度参数的尺寸效应进行了研究。

表1 岩块和结构面模拟参数

Table1 The parameters of rock and discontinuities in the models

岩体内摩擦角φ/(°)黏聚力c/kPa变形模量E/MPa泊松比υKs/GPaKn/GPa抗拉强度σt/kPa岩块40.02.0170.00.22——2.4结构面30.01.0——1.01.0—

本文利用数值模拟软件FLAC3D，建立节理岩体试样模型，对单轴压缩下含不同结构面组数、不同结构面倾角试样的强度、变形、破坏方式等特征进行了系统研究。

1 数值模拟方法

本模拟试验岩块剪断和结构面滑动破坏准则均采用Mohr-Coulomb线性抗剪和抗拉强度准则。FLAC3D中利用Interface作为接触面模拟岩体中的结构面，在数值计算中，Interface的参数包括黏聚力、摩擦角、剪胀角、法向刚度、切向刚度、抗拉强度(Itasca Consulting Group Inc.，2002)。本次数值模拟试验所用计算参数(表1)。

数值模拟试验试样x、y和z方向尺寸分别为3m×1m×6m，试验中，控制xz面y方向的位移为0m·s-1，在xy端面z方向相向加载，初始加载速率为1×10-8m·s-1。加载过程中，利用FLAC模拟软件内置Fish语言编写伺服控制程序，通过调节加载速率控制试样内部最大不平衡力为1～4N。运行过程中，采集试样加载面不平衡力数据，除以试样断面面积，可以得到试样承受的应力； 同时，监测试样加载面之间的位移量，除以试样加载面之间距离，可以得到试样的应变。当试样的应力-应变曲线达到峰值强度时，试样开始屈服。

图2 含贯通性结构面试样模型

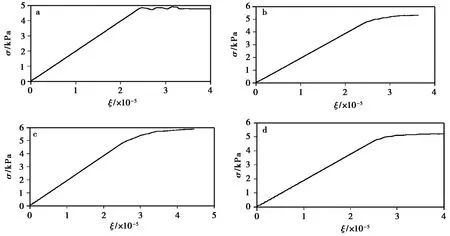
图3 含贯通结构面试件应力-应变曲线

2 含贯通性结构面试样

Halakatevakis et al.(2010)利用UDEC对含结构面试件进行了数值模拟，结论显示数值模拟试验中同组结构面数量对试样强度没有影响。本文对含单组不同数量结构面试样进行模拟发现随着结构面数量的增加，变形模量逐渐减小，但强度基本不变。为简便，在本研究中，分别建立如图2 所示模型，模型中结构面组数分别为1～4组，除了对结构面密度效应的研究外，模型中每组所含结构面条数均为1。试验中，对于不同组模型，保持结构面之间的夹角不变，变化其中一条结构面与最大主应力方向的夹角β(每隔5°建立一个模型)，形成不同的结构面试样模型，研究不同组数、不同倾角结构面试件的变形强度特征。

2.1 应力-应变曲线特征

从全应力-应变曲线可以看出，含单组贯通性结构面试样应力达到峰值强度后，稍微波动并稳定，图3a； 含多组贯通性结构面试件有应变硬化现象，图3b～图3d。

2.2 破坏方式

对于岩体的破坏方式，孙广忠(1988)总结为3类：结构面控制，部分由结构面控制，不由结构面控制。图4 为含单条贯通性结构面试样的3种不同破坏形式。经统计，随着试样内结构面组数的增加，岩体破坏受结构面控制的概率增加(图5)。

图4 3类含单组贯通结构面试样破坏方式

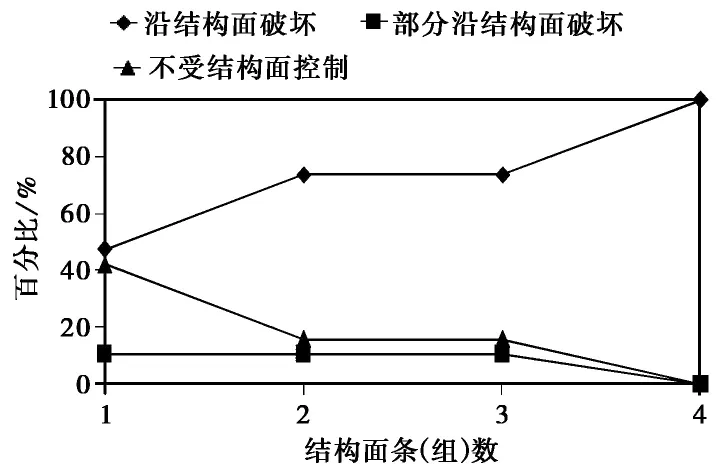
图5 试样破坏方式与结构面组数之间的关系

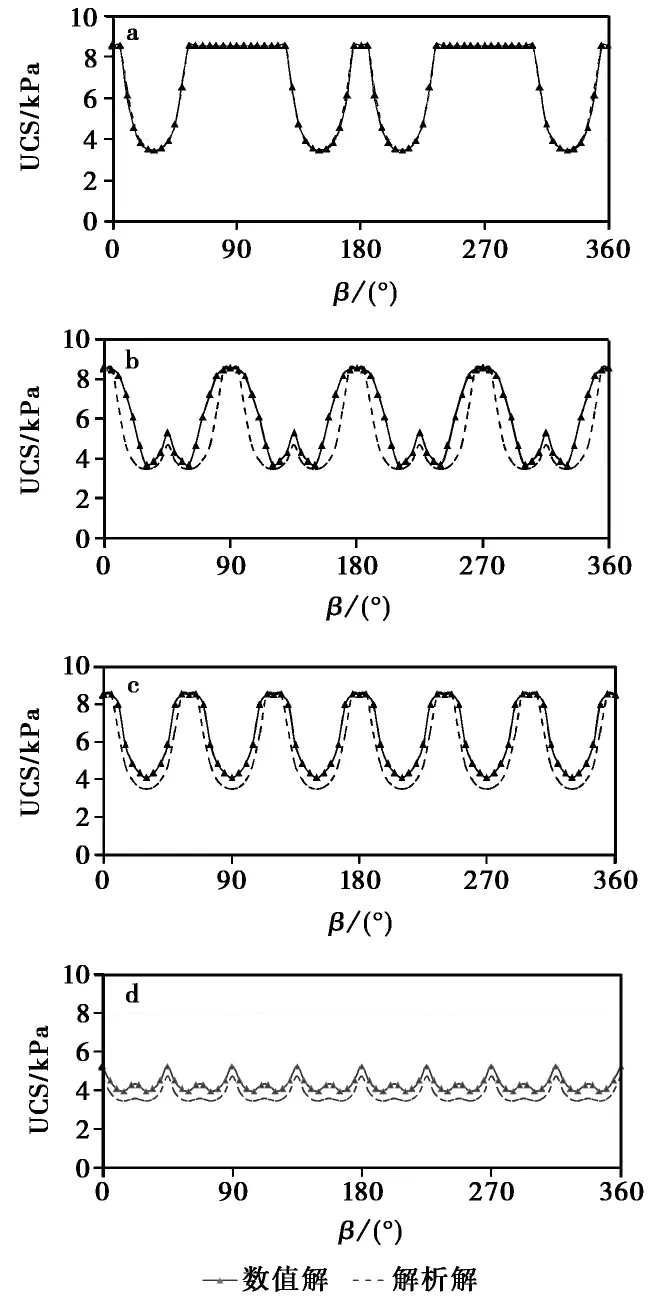
图6 含不同组贯通结构面试样抗压强度随β变化规律

2.3 强度特征

数值模拟解与解析解对比可以发现，含单条结构面试样的数值解与Jaeger解析解一致，而含多条结构面试样的数值解在结构面控制破坏时，均大于Jaeger解析解，这是因为多条结构面相互之间的耦合作用，增大了试样沿结构面破坏的阻力。由图6 也可以看出，岩体中含有3组及以下结构面时，各向异性较明显，含4组结构面时，岩体呈现出各向同性特征，这与Hoek-Brown提出的含4组以上性质相近结构面的岩体，在地下开挖工程设计中可以按各向同性岩体来处理的观点是一致的。

2.4 结构面密度效应

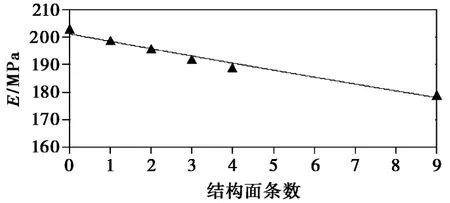
图7 同一尺寸试样结构面条数与变形模量关系

结构面密度效应，即对同一尺寸岩体来说，岩体力学参数随着岩体结构面密度增大而减小。本文模拟试验结构表明，对于不同组结构面，随着组数的增加，岩体强度减小，变形模量减小； 对于含一组结构面的岩体试件，本文分别建立了含1条、3条、9条β=45°时的结构面试样模型，随着结构面条数的增加，岩体强度变化不大，变形模量减小； 含单组3条结构面试样与含3组单条结构面试样的变形模量基本相等，说明在岩块和结构面参数一定的情况下，岩体结构面密度是控制岩体变形的主要因素(图7)。以上结论与晏长根等(2009)所得结果一致。

3 含非贯通性结构面试验

为研究非贯通性结构面试样单轴压缩情况下的强度变形特征，本文根据结构面倾角，每隔5°建立一个如图8 所示试样模型，试样中均含单条结构面，中点为试样中心点，除研究结构面连续性对试样强度变形特征影响外，结构面迹长均为2m。

图8 含单组非贯通性结构面试样模型

3.1 应力-应变曲线特征

含非贯通性结构面试样应力-应变曲线出现的最大特征为在β为0°～15°和60°～90°时，应力达到峰值后出现应力降，表现出应变软化现象(图9a)； 而当β在25°～50°之间时，则出现应变硬化现象或达到峰值强度后保持不变(图9b)；β在15°～25°和50°～60°时，应力-应变曲线为过渡形式(图9c)。经观察试样的破坏情况，这一结果可能是当β较大或较小时，非贯通结构面尖端在荷载作用下出现拉裂，最后裂纹扩展贯通，试样突然破坏，出现应力降； 而当β处于25°～55°之间时，试样则发生沿非贯通结构面剪切破坏，试样不会出现突然破裂； 图9c的情况则是结构面拉剪结合破坏模式的结果。

图9 非贯通结构面试样应力-应变曲线

3.2 破坏模式

同贯通性结构面试件类似，本文将非贯通性结构面试件的破坏模式分为3类：结构面控制型破坏，结构面部分控制型破坏，及结构面不控制型破坏(图10)。

图10 含非贯通结构面破坏方式

3.3 强度特征

对于非贯通结构面试样的抗压强度，断裂力学中，利用Griffith准则可以判断裂纹的起裂强度，但是裂纹起裂并不能代表试样破坏，因此岩体强度用Griffith破坏准则刻画是不合适的。现阶段，大多采用损伤理论来处理这一问题(孙广忠，1988)：

(4)

式中，A为岩体受σ1作用的总面积；σ1b为完整岩块的强度；a为完整岩块发挥抵抗力作用部分的面积；σ1j为结构面发挥作用部分的强度；b为结构面发挥抵抗作用部分的面积(图11)。

图12为本次数值模拟与按以上解析方法计算的随着β变化的强度图，从图中可以看出，当β=0°～5°及55°～90°时，解析解与数值解相等，结构面对试样强度基本无影响；当β=5°～30°时，解析解比数值解略大，经查看试样的破坏形式及应力状态发现，此时结构面尖端产生较大的拉应力，产生拉裂破坏，而解析解未考虑拉应力，造成对结果偏大；当β=30°～55°时，数值解大于解析解。

图11 含非贯通结构面试样力学模型

图12 含非贯通结构面试样强度

3.4 连续性

为研究试样中结构面贯通性对试样变形强度参数的影响，建立含不同迹长非贯通结构面模型(图8)β=45°。数值模拟结果发现，随着结构面迹长(连通率)的增加，试样的单轴抗压强度和变形模量均降低(图13)。

图13 试样单轴抗压强度和变形模量与结构面连通率的关系(β=45°)

4 结论与讨论

基于FLAC3D数值模拟软件建立了含贯通性结构面和非贯通性结构面的试件模型，并分别进行了单轴压缩模拟试验，得到了如下结论：

(1)对于含贯通结构面试件，含两组及以上结构面的岩体其应力-应变曲线有应变硬化现象； 含3组及以下结构面试样各向异性特征显著，而4组及以上结构面试样呈现各向同性特征； 含两条及以上结构面试样的强度，数值解比Jaeger解析解大； 含结构面试件单轴压缩下破坏方式主要有3种，分别为结构面控制破坏，结构面不控制破坏和部分由结构面控制的破坏； 对同尺寸岩体，其变形强度参数随结构面数量的增多而劣化。

(2)对于含非贯通结构面试验，β较大或较小时，应力-应变曲线出现应力降； 试样单轴抗压强度随着结构面角度变化呈现各向异性特征，数值模拟解与基于剪切准则和损伤理论的解析解相比，在β=5°～30°时，解析解比数值解略大，当β=30°～55°时，数值解大于解析解； 随着结构面迹长的增大，试样变形强度参数下降。

Bobet A，Einstein H H. 1998. Fracture coalescence in rock-type materials under uniaxial and biaxial compression[J]. International Journal of Rock Mechanics and Mining Sciences， 35(7)： 863～888．

Cai M，He M，Liu D. 2009. Rock mechanics and engineering[M]. Beijing： Science Press.

Einstein H H，Nelson R A，Bruhn R W，et al. 1970. Model studies of jointed rock behavior[C]∥Proceedings of the 11th US rock mechanics symposium. Berkeley， California：[s.n.]： 83～103．

Halakatevakis N，Sofianos A I. 2010. Strength of a blocky rock mass based on an extended plane of weakness theory[J]. International Journal of Rock Mechanics & Mining Sciences， 47(4)： 568～582.

Hoek E，Brown E. 1980. Empirical strength criterion for rock mass[J]. Journal of Geotechnical Engineering ASCE.，106： 1013～1035．

Hoek E. 1986. Strength of rock and rock masses[J]. ISRM News Journal，16： 1～73.

Hudson J A，Hurrison J P. 2000. Engineering rock mechanics-an introduction to the principles[M]. Oxford： Pergamon Press．

Itasca Consulting Group Inc. 2002. FLAC3D(Fast LagrangianAnalysis of Continua in 3 Dimensions) User Manuals， Version 2.1[M]. Minneapolis， Minnesota．

Jaeger J C. 1960. Shear fracture of anisotropic rocks[J]. Geological Magazine，97： 65～72.

John K W. 1969. Festigkeit und Verformbarkeit von druckfesten， regelmassig gefugten Diskontinuen[J]. International Soil Mechanics & Rock Mechanics， University of Karlsruhe， Karlsruhe， Heft 37．

Ladanyi B，Archambault G. 1972. Evaluation de la resistance au cisaillement d’un massif rocheux fragmente[C]∥Proceedings of the 24th International Geological Congress. Montreal：[s.n.]: 249～260．

Müller L，Pacher F. 1965. Modellversuche zur klarung der bruchgefahr geklüfteter medien[J]. Rock Mechanics and Engineering Geology， (S2)： 7～24.

Nasseri M H B，Rao K S，Ramamurthy T. 2003. Anisotropic strength and deformational behavior of Himalayan schists[J]. International Journal of Rock Mechanics & Mining Sciences， 40(1)： 3～23．

Pomeroy C D，Hobbs D W，Mahmoud A. 1971. The effect of weakness-plane orientation on the fracture of Barnsley Hards by triaxial compression[J]. International Journal of Rock Mechanics & Mining Sciences，8(3)： 227～238．

Sun G. 1988. Rock mass structural mechanics[M]. Beijing： Science Press．

Vasarhelyi B，Bobet A. 2000. Modeling of crack initiation， propagation and coalescence in uniaxial compression[J]. Rock Mechanics and Rock Engineering，33(2)： 119～139．

Wong L N Y，Einstein H H. 2009. Crack coalescence in molded gypsum and carrara marble： part 1.macroscopic observations and interpretation[J]. Rock Mechanics and Rock Engineering，42： 475～511．

Xiang T B， Feng X T， Chen B R， et al. 2009. Rock failure mechanism and true triaxial experimental study of specimens with single structural plane under three-dimensional stress[J]. Rock and Soil Mechanics，30(10)： 2908～2916．

Yan C G，Wu F Q，Qi S W，et al. 2009. Deformation and strength parameters and size effect of random jointed rock mass by numerical simulation[J]. Chinese Journal of Geotechnical Engineering，31(6)： 879～885．

蔡美峰，何满潮，刘东燕. 2009. 岩石力学与工程[M]. 北京：科学出版社．

孙广忠. 1988. 岩体结构力学[M]. 北京：科学出版社．

向天兵，冯夏庭，陈炳瑞，等. 2009. 三向应力水平状态下单结构面岩石试样破坏机制与真三轴试验研究[J]. 岩土力学，30(10)： 2908～2916．

晏长根，伍法权，祁生文，等. 2009. 随机节理岩体变形与强度参数及其尺寸效应的数值模拟研究[J]. 岩土工程学报，31(6)： 879～885．

JournalofEngineeringGeology工程地质学报 1004-9665/2016/24(5)- 0899- 08

STRENGTH AND DEFORMATION CHARACTERISTICS OF ROCK SAMPLE WITH DISCONTINUITIES UNDER NUMERICAL UNIAXIAL COMPRESSION SIMULATION TESTS

The discontinuities are the key factors that differentiate the rock mass and intact rock. The mechanical behaviours of rock mass are strongly affected by length， occurrence and consistency of the discontinuities. Characteristics-deformation， strength， failure modes of rock samples with various discontinuities under uniaxial compression have been studied based on the numerical modelling FLAC3D.Rock samples with different groups of penetrated discontinuities and different unpenetrated discontinuities have been set up. On the basis of these models， a number of numerical uniaxial compression tests have been carried out， in which the shear and tensile strength criterion(Mohr-Coulomb criterion) has been used. During the uniaxial compression simulation tests， a servo-control program is used to restrict the maximum unbalanced force through adjusting the applied velocity. The results of simulation tests are shown as follow： rock samples with fewer than 4 groups of penetrated discontinuities are anisotropic while those with 4 groups of penetrated discontinuities are nearly isotropic. The deformation and strength parameters get lower as the number of penetrated discontinuities get higher in rock sample with same size. Stress drop is observed after peak stress in the stress-strain curve of rock sample with unpenetrated continuity. Uniaxial compressive strength derived from simulation is different from that calculated by analytic method based on shear strength and damage theory， which indicates that shear strength criterion may be not suitable for rock mass with unpenetrated discontinuities. The deformation and strength parameters get lower as the continuity trace length bigger. The failure modes of rock samples with discontinuities can be divided into three types： discontinuity-controlled， discontinuity-half controlled and discontinuity-uncontrolled. As the number of groups increases the failure are more likely to be discontinuity-controlled.

Rock mass， Strength， Deformation， Uniaxial compression， Discontinuities

10.13544/j.cnki.jeg.2016.05.019

2016-05-27;

2016-07-23.

国家自然科学基金(41322020， 41172272， 41302234)，中国博士后科学基金(2015M581167)资助.

郭松峰(1986-)，男，博士，博士后，主要从事岩体力学及工程地质方面的工作. Email: guosongfeng@mail.iggcas.ac.cn

P642.3

A