一种基于压缩感知的迭代重建算法

李 影，徐伯庆

(上海理工大学 光电信息与计算机工程学院，上海 200093)



一种基于压缩感知的迭代重建算法

李 影，徐伯庆

(上海理工大学 光电信息与计算机工程学院，上海 200093)

迭代重建算法是一种经典的CT图像重建算法，适合于不完全投影数据的图像重建，其缺点是重建速度慢。为提高图像重建的质量和速度，文中利用压缩感知理论提出了一种改进的基于图像全变差最小的迭代重建算法。该算法在迭代的不同阶段对迭代初始值做不同处理，并在每次迭代结束后采用梯度下降法调整全变差。实验结果表明，该算法不但提高了图像重建质量，同时也加快了迭代图像的收敛速度。

迭代重建算法；压缩传感；图像全变差

迭代图像重建算法是一种经典的CT图像重建算法，其优势主要体现在投影数据不完全或投影角度缺失的情况下，该算法仍能获得高质量的重建图像，其缺点是重建速度慢[1]。随着并行计算理论及计算机技术的快速发展，迭代重建算法低速率的缺点已经变成次要矛盾[2]。如何重建出更高质量的图像获得更优的算法性能，才是目前图像重建领域内学者们致力研究的问题。

近年发展起来的压缩感知(Compressed Sensing，CS)理论表明，若图像能在某个变换域稀疏表示，则可由远少于奈奎斯特采样数的投影观测值足够清晰地重建出原始图像[3]。对于医学CT图像，由于同一器官内部组织差异性较小，图像具有局部平滑性，对其进行有限差分(Finite Difference)变换后，图像符合稀疏条件[4]。

本文在经典的迭代重建算法ART的基础上，利用压缩感知理论提出了一种改进的基于图像全变差最小的迭代重建算法，并通过Shepp-logan头模型仿真结果验证了该算法的有效性。

1 传统ART算法基本原理

ART算法先离散化重建模型，将待重建图像f(x,y)看成是由N=n×n个正方形的非重叠的像素格组成的[5]，每个正方形的像素格的边长为1，在每个像素格里的像素值是一个常数，用fj(1≤j≤M)表示第j个像素格的像素值。若用pi表示第i条射线的投影值，用wij表示第j个像素对第i条射线投影值的贡献，即权重因子。根据成像的物理过程和相应的数学模型，则图像向量f和投影向量p的关系可表示为

(1)

式(1)可用矩阵表示为

wr=p

(2)

代数方程组(1)一般采用迭代的方法来进行求解[6]。迭代公式为

(3)

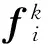
2 基于压缩感知的迭代重建算法

由压缩感知理论与图像重建的基本原理可知，二维CT图像可通过求解如下有约束的最小化问题进行重建[7-8]

min‖ΨX‖l1s.tΦX=Y

(4)

其中，X为待重建图像，X∈RN；Y为观测向量，Y∈RM；Ψ为稀疏变换矩阵；Φ。由于CT梯度图像具有稀疏性的先验知识，常将其有限差分变换的 范数，即全变差(Total Variation，TV)作为优化问题的目标函数[9]。若用f表示二维CT图像，则其全变差为

‖f‖TV=∑i,j((fi,j-fi-1,j)2+(fi,j-fi,j-1)2)1/2

(5)

用N维向量F表示图像，此时重构问题转化为

min‖F‖TVs .tWF=P

(6)

其中，W为系统矩阵；P为投影数据。

文献[10]先用传统代数迭代重建算法得到满足约束条件的原始图像，然后在每次迭代结束后采用梯度下降法调整全变差，循环迭代得到最终图像，可称为ART-TVM算法。

本文在ART-TVM算法的基础上，将此算法分成两个阶段，并根据投影角度数来设定迭代次数的临界值，令k为整个算法的迭代次数，c为迭代次数的临界值。当迭代次数k小于临界值c时为第一阶段，将前一次完整迭代过程中所有子迭代值的平均值作为下一次迭代的初始值，使TVM所依赖的初始估计图像达到一定质量，在此基础上，TVM修正更为有效；当迭代次数k≥临界值c时为第二个阶段，为了保持图像的边缘，后几次迭代不再进行平滑处理。

本文算法流程如下：

用f(k)表示第k次完整迭代结果;f(k)(i)表示第k次迭代过程中第i个方程的计算结果。

(1)对投影角度进行排序，使相邻的访问角度尽可能正交，从而加快收敛速度；

(2)将待重建图f初始化，f(k=0)=0；

(3)按照式(3)，对f进行一次完整的迭代，得到f(k)；

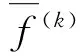
3 实验结果对比分析

实验采用Shepp-logan头模型图像进行仿真验证，图像尺寸大小为128×128。下面将给出3组实验，对传统ART算法、ART-TVM算法以及本文中改进的TVM算法分别在180，90和30个投影角度进行比较。本文算法中的松弛因子，步长因子以及临界值c在不同投影角度数下的设置如表1所示。

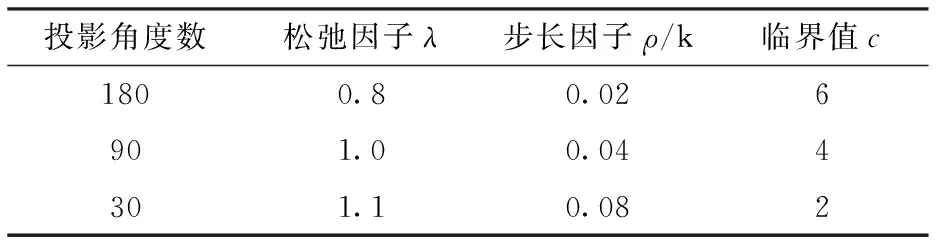
表1 不同投影角度数下的参数设置

实验1 在这组实验中，投影角度数为180个，图1为传统ART算法与ART-TVM算法以及本文算法的PSNR值随迭代次数的变化曲线图。并在图2中分别列出了3者在不同次数迭代之后的重建结果。

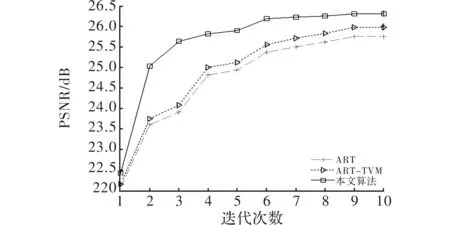
图1 180个投影角PSNR值变化曲线

图2 180个投影角迭代结果图比较

实验2 在这组实验中，投影角度数为90个，图3中为传统ART算法与ART-TVM算法以及本文算法的PSNR值随迭代次数的变化曲线图。并在图4中分别列出了3者在不同次数迭代之后的重建结果。

图3 90个投影角PSNR值变化曲线

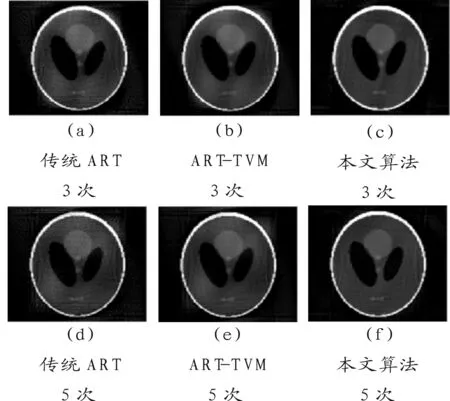
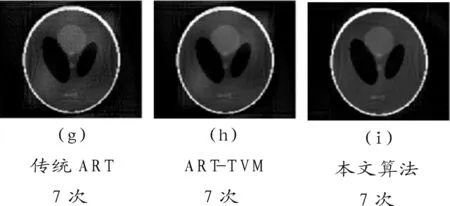
图4 90个投影角迭代结果图比较

实验3 在这组实验中，投影角度数为30个，图5中为传统ART算法与ART-TVM算法以及本文算法的PSNR值随迭代次数的变化曲线图。并在图6中分别列出了3者在不同次数迭代之后的重建结果。

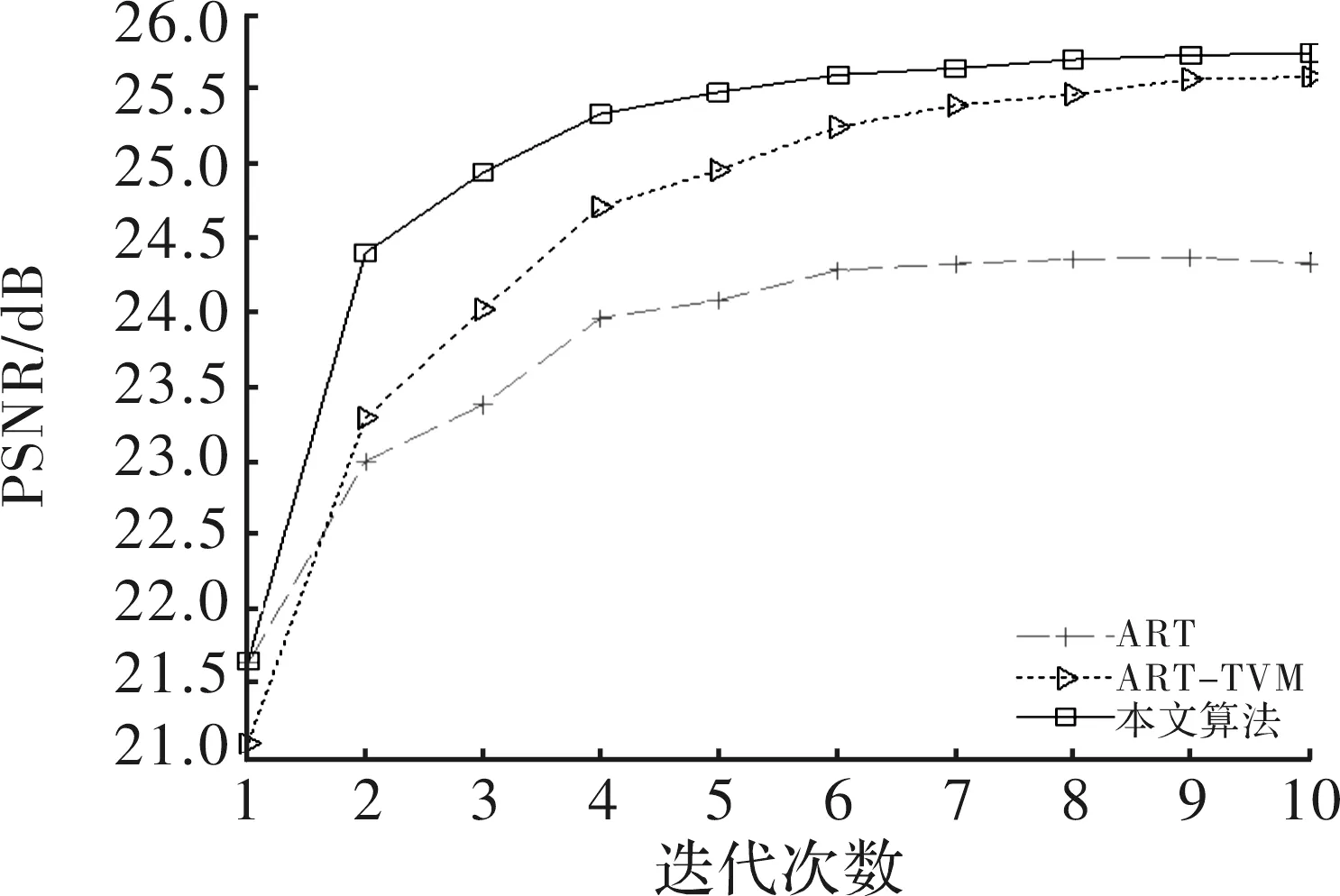
图5 30个投影角PSNR变化曲线

图6 30个投影角迭代结果图比较

由以上3组实验可看出，在相同投影角度数下达到相同PSNR 时, 本文算法所需要的迭代次数远少于传统ART 算法以及ART-TVM算法，本文算法能更快地达到较好的质量，在前几次迭代时重建质量提高得比较快，一般迭代了6、7次后PSNR值就能趋于平稳。此外，相比于传统的ART-TVM算法适用于投影角度稀疏的情况，本文中改进的TVM算法不仅适用于少量的投影角度，也同样适用于较完备的投影角度。

4 结束语

本文利用压缩感知理论提出了一种改进的基于图像全变差最小的迭代重建算法。该算法在迭代的不同阶段对迭代初始值做不同处理，并在每次迭代结束后采用梯度下降法调整全变差。对Shepp-logan标准CT 模型图像进行重建的实验结果表明，本文算法重建图像的峰值信噪比和主观视觉效果均优于传统的ART 算法与ART-TVM算法，值得进一步深入研究。

[1] 郭威.CT不完全投影数据重建算法研究[D].长春:吉林大学,2011.

[2] 李志鹏,丛鹏,邬海峰.代数迭代算法进行CT图像重建的研究[J].核电子学与探测技术,2005,25(2):184-186.

[3] Candès E J.Compressive Sampling[J]. Marta Sanz Solé,2006,17(2):1433-1452.

[4] Candès E J,Romberg J,Tao T.Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J].IEEE Transactions on Information Theory,2004,52(2):489-509.

[5] 刘晓,钱达志,卢铁城.CT图像重建算法的比较研究[C].西安:第十三届反应堆数值计算与粒子输运学术会议暨反应堆物理会议,2010.

[6] Gordon R,Bender R,Herman G T. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and X-ray photography[J].Journal of Theoretical Biology,1970,29(3): 471-481.

[7] Sidky E,Pan X.Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization[J].Physics in Medicine & Biology,2008, 53(17):4777-807.

[8] Candès E J,Romberg J K,Tao T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure & Applied Mathematics,2006,59(8):1207-1223.

[9] Ludwig R,Frank B,Christof F,et al. Improved total variation-based CT image reconstruction applied to clinical data[J]. Physics in Medicine & Biology, 2011, 56(6):1545-1561.

[10] 练秋生,郝鹏鹏.基于压缩传感和代数重建法的CT图像重建[J].光学技术,2009,35(3):422-425.

An Iterative Image Reconstruction Algorithm based on Compressed Sensing

LI Ying, XU Boqing

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China)

The iterative image reconstruction algorithm is a classic method for the image reconstruction of computed tomography (CT), which can recover the image from incomplete projection data. However, the Iterative image reconstruction algorithm suffers slow reconstruction speed. With the theory of compressed sensing, an improved algorithm based on the minimization of the image total variation (TV) is proposed to improve the quality of the recovered image and the speed of reconstruction. In the improved algorithm, the initial value of iteration differs in different stages of the iteration, and the total variation is adjusted by the gradient descend method after each iteration. Experimental results indicate that the proposed algorithm not only improves the quality of image reconstructed, but also increases the convergence speed of the iteration image.

iterative image reconstruction algorithm; compressed sensing; image total variation

2016- 01- 22

李影(1990-)，女，硕士研究生。研究方向：信号与信息处理。徐伯庆(1958-)，男，博士，副教授。研究方向：通信及图像处理。

10.16180/j.cnki.issn1007-7820.2016.11.037

TN919.8；TP391.41

A

1007-7820(2016)11-129-04