FFT在大型风电机组自适应控制中的应用

邬昌明，王文卓，高 昆，芦 健

(国电南瑞科技股份有限公司，江苏 南京 211100)



FFT在大型风电机组自适应控制中的应用

邬昌明，王文卓，高 昆，芦 健

(国电南瑞科技股份有限公司，江苏 南京 211100)

在大型风电机组传动系统降载控制策略中的滤波和加阻等方法均需要机组传动链扭振频率，而实际机组运行过程中的扭振频率难以精确获取。文中通过FFT实时分析发电机转速，提出通过计算能量密度自动判断振动的方法，实时监测风机扭振并计算振动频率。将计算结果作为风电机组自适应控制滤波和加阻的依据，使用该方法对实际的运行数据进行计算，计算结果验证了该方法能有效的监测风机扭振并计算出振动频率。

FFT；扭振；自适应控制；能量密度

随着风电机组单机容量不断增大，叶片、传动系统和塔架等主要部件的柔性显著增加，主要零部件的固有频率逐渐下降，机组运行过程中所受的动态载荷越来越复杂，传动系统发生扭振的几率呈升高的趋势[1]。扭振可能引起传动系统扭矩波动，造成主要零部件疲劳损伤，降低机组使用寿命[2]。采取有效措施抑制传动系统，减小扭转载荷导致的传动系统疲劳损伤已成为风电机组控制领域的研究热点。文献[3]在发电机转矩控制器中添加了阻尼滤波器，提高控制器阻尼，降低传动系统扭矩波动的幅度；文献[4]通过卡尔曼滤波器对传动系统扭振幅度进行估计，进而通过对发电机转矩控制来抑制传动系统扭振。这两种方法都是基于传动系统的线性化模型，难以真实地反映风电机组传动系统的动态响应，存在一定的局限性。文献[5]分析了风电机组对风速波动的滤波特性，并指出风速扰动或电网扰动都能引起轴系振荡，且实际的轴系振荡频率因为受到阻尼因数的影响，不完全等于自然振荡频率。所以，固定频率的阻尼加载或陷波器滤波不能适应风机在不同条件下的需求，需要一个能够动态检测风机传动链扭振频率的方法来保证附加阻尼或滤波器的准确性。

1 传动链扭振危害及抑制

在大型旋转机械系统中，传动链扭振是一个普遍存在的问题。风力发电机正常工作时，由于风载不是恒定的，风速大小和风向实时变化，因此，风电机组传动链中传递的扭矩也随机波动。同时，风电机组传动链较长，功率传递需要经过轮毂、主轴、齿轮箱、联轴器和发电机，由于传递的载荷较大，联轴器是复合材料制成等因素，传动链的扭转刚度相对较小。传动链不能简化成刚体，而应视为一个复杂的弹性连续体进行研究和分析。在非平衡载荷的作用下，柔性传动链容易出现扭振。严重的扭振可能会导致轴类零件的疲劳损坏，甚至断裂；导致齿轮运转噪声增大，出现齿面点蚀、齿与齿的冲击甚至轮齿断裂；联轴器损坏，表现为弹性元件的过热或碎裂等。

传动链工作过程中，当系统的激励频率与传动链轴系的固有频率接近时，其扭转振动的振幅会迅速增大，出现共振现象。零部件发生共振是任何机械装备不允许出现的，共振对机械设备的危害极大，强烈的共振可能直接毁坏设备，图1所示为由于传动链扭振导致的联轴器打滑损坏。

图1 扭振损坏的联轴器

所以在控制过程中，对传动系统的扭振检测和通过控制降低扭振，是必要的。文献[6]指出采用发电机转速反馈信号的转速控制模式和采用风轮转速反馈信号的恒功率控制模式能提供良好电气阻尼，抑制轴系振荡。文献[7]讨论了在转速控制策略下，控制器参数对轴系振荡的影响。双馈风电机组通常采用高速轴转速作为控制反馈，通过陷波器对反馈转速做相应频率的滤波处理，剔除或减小控制环对扭振频率的响应来避免共振。对于滤波无法解决的振动问题，在发电机给定转矩上附加一个与扭振波动反相的额外转矩 ，从而加大整个传动链的等效阻尼，抑制传动链扭转振动[8]。这两种方式均需要以传动链的扭振频率作为基础进行添加。

2 分析处理方法

2.1 离散傅里叶变换

通过离散傅里叶变换(DFT)，能用连续信号处理不可能使用的方法来分析、操作和合成信号。DFT是一个确定离散信号序列中所包含的谐波或者频率成分的数学工具。在时域中对连续信号进行周期采样就能得到离散序列，无论该序列的实际意义如何，DFT对离散序列的分析都是有意义的[9]。

假设x(t)是一个包含无数个复正弦的时域连续周期信号，其傅里叶变换为

(1)

其傅里叶反变换为

(2)

由式(1)和式(2)可知，X(jw)是w的连续函数，称为信号x(t)的频谱密度函数，简称频谱。 计算机只能对离散的有限长信号进行频谱分析，对傅里叶变换对进行时域和频域的离散化，即将t=nΔt和w=k2πΔf分别代入式(1)和式(2)，可得DFT变换对为

(3)

(4)

因此，对任一有限长时域序列，都可按式(3)在计算机上求其频谱。

2.2 快速傅里叶变换

虽然DFT是确定时域序列频率成分最直接的数学过程，但其运算效率较低。例如式(3)，求一点X(k)，需要计算N次复数乘法，求两点X(k)，则需要计算N2次复数乘法。随着DFT输入点数增加到数百或数千，DFT需要的计算量就更大，这大幅影响了计算的实时性。快速傅里叶变换(FFT)是DFT的一种快速算法，利用DFT的周期性和对称性，将一个N项序列(设N=2k，k为正整数)，分为两个N/2的子序列，这样变换后运算次数就变成N+N2/2次，以此类推将这种一分为二的思想不断进行下去，直至分为两两一组的DFT运算单元，则N点DFT变换就只需Nlog2次运算[10]。FFT能确保在风电机组控制系统内实现，且不对系统的运行造成影响。

2.3 能量密度

通过FFT进行时域到频域的转换后，为确定特征频率，通常通过绘制功率谱来进行分析，考虑到实际应用的需求，本文提出通过计算能量密度的方式来判断是否存在扭振和计算扭振频率。

(5)

考虑到转速波动相对于实际转速而言比较小，所以在进行能量密度分析时将第一个值(直流分量)置0，即|F(0)|=0。计算能量密度

(6)

根据相应能量密度尖峰数组序号可以得到相应的频率。

通过能量密度的大小来判断是否存在相应频率的振动，同时能量密度将所有的频率能量折算到相同的百分比内，有利于通过设定固定的阈值来判断是否存在扭振现象，进而得到相应的扭振频率。

3 分析结果和仿真验证

根据上文提出的分析方法在控制程序中实现并通过对现场采样的数据进行验证，实际转速曲线如图2～图4所示，曲线的采样周期为20 ms，为便于计算，在曲线中分别选取其中的1 024个连续点进行计算。

图2 典型的扭振现象转速曲线

图3 存在干扰信号的转速曲线

图4 正常无干扰转速曲线

计算分析结果如图5～图7所示，从图5可看出,图2曲线中存在明显的扭振现象，扭振频率为2.1 Hz。图3曲线所示的转速虽然也有上下波动，但不是固定频率额波动，图4的曲线比较光滑，所以图6和图7的分析结果中均无明显的扭振特征频率。

图5 扭振曲线能量密度

图6 干扰信号曲线能量密度

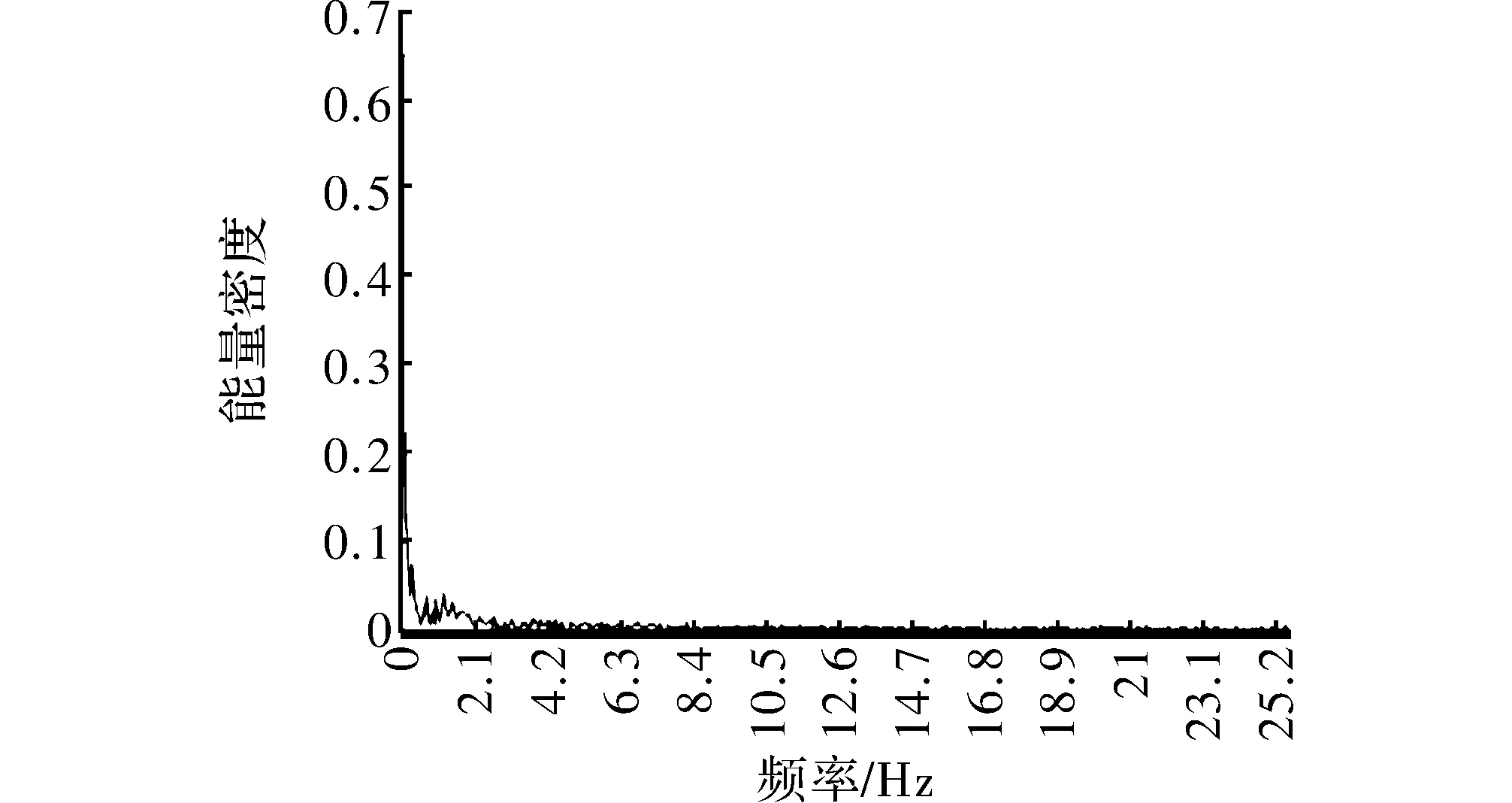
图7 正常曲线谱能量密度

4 结束语

通过FFT对发电机转速进行处理，使用能量密度的计算后能准确的检测传动链扭振并获取扭振频率，为传动链降载控制所需的滤波和加阻提供了数据依据，并可提高控制精度，有效延长风机使用寿命。同时，本文将不同频率的能量密度折算到相同的比例之下，也便于在控制系统内进行量化的判断和对比分析。

[1] 姚兴佳,王晓东,单光坤,等.双馈风电机组传动系统扭振抑制自抗扰控制[J].电工技术学报,2012,27(1):136-141.

[2] Burton T,Sharpe D,Jenkins N，et al.Wind energy handbook[M].New York: John Wiley & Sons,Ltd,2001

[3] 邢作霞,刘颖明,郑琼林,等.基于阻尼滤波的大型风电机组柔性振动控制技术[J].太阳能学报,2008,29(11):1425-1431.

[4] Eric Van Der Hooft,Schaak P.Wind turbine control algorithm[R].Netherlands:Energy Research Center of the Netherlands,2003.

[5] Akhmatov V,Knudsen H,Nielsen A H．Advanced simulation of windmills in the electric power supply [J].Electrical Power and Energy Systems,2000,22(6):421-434.

[6] 张琛,李征,高强,等.双馈风电机组的不同控制策略对轴系振荡的阻尼作用[J].中国电机工程学报,2013,33(27):135-144.

[7]AkhmatovV.Variable-speedwindturbineswithdoubly-fedinductiongeneratorsPartII：powersystemstability[J].WindEngineering,2002,26(3):171-188.

[8] 何玉林,苏东旭,黄帅,等.变速变桨风力发电机组的桨距控制及载荷优化[J].电力系统保护与控制,2011,39(16):95-100.

[9] 王世一.数字信号处理[M].北京:北京理工大学出版社,1997.

[10]GenmtlemanWM,SandeG.Fastfouriertransformforfunandprofit[C].Germany:AFIPSProceedingFallJointComputerConference,1966.

Application of FFT in Adaptive Control of Large Wind Turbines

WU Changming, WANG Wenzhuo, GAO Kun, LU Jian

(NARI Technology Development Co. Ltd., Nanjing 211100, China)

The filtering and damping in the control strategies of drive train load reduction in large wind turbines requires the acquisition of the accurate torsional vibration frequency, which is difficult to obtain in running wind turbines. The article proposes a method for detecting the torsional vibration and obtaining the vibration frequency by analyzing the generator speed by FFT and calculating the energy density. Finally, actual data are calculated by this method, and the results verify that the method can effectively monitor torsional vibration and calculate the vibration frequency.

FFT; Torsional vibration; adaptive control; energy density

2016- 01- 18

邬昌明(1982-)，男，硕士，工程师。研究方向：风力发电机组控制技术。

10.16180/j.cnki.issn1007-7820.2016.11.019

TM614

A

1007-7820(2016)11-062-04