木质粉末冷模压成形致密化过程数值模拟

彭 博，陈 飞，辜良瑶，吴庆定

（中南林业科技大学，湖南 长沙 410004）

木质粉末冷模压成形致密化过程数值模拟

彭 博，陈 飞，辜良瑶，吴庆定

（中南林业科技大学，湖南 长沙 410004）

为探寻木质粉末模压成形致密化规律，以杨木粉末和芦苇粉末为试材，重点基于室温模压成形试验数据，借助有限元法分析了成形压力对木质粉末压坯密度的影响规律。结果表明：在弹塑性理论的理想假设下，Shima模型适合木质粉末冷模压成形致密化过程数值模拟，试验结果与理论模型计算数据高度吻合，可用于指导木质粉末热模压成形致密化过程研究。

木质粉末；冷成形；致密化；数值模拟

国内外关于粉体材料模压成形致密化过程的数值模拟研究已有几十年的历史，但基于木质粉末相关研究的公开报道并不多见[1-5]。尽管已有的研究成果大多基于理想化的“可压缩连续体”粉体原料建立起的系列理论准则，例如：Kuhn等提出的多孔介质模型[6]、Shima材料模型[7]、Doraivelu准则[8]、Kim准则[9]等；但由于非连续介质的力学基础并不完善，使得这些理论准则在粉体材料成形领域的应用受到了很大制约。本文拟基于粉体材料连续性假设，以芦苇和杨木的粉末为例，借助Shima模型运用MSC.MACR有限元分析软件对木质粉末在室温条件下的模压成形致密化过程实施模拟分析[10]，从而建立木质粉末冷模压成形致密化过程的数值模型，为木质粉末热模压成形致密化过程建模打下坚实基础。

1 木质粉末颗粒的物理特征

1.1 试验材料

杨木： 30 kg，采集于湖南常德市斗姆湖林区。芦苇：30 kg，采集于湖南浏阳市大围山区。

1.2 主要设备与仪器

F160型号试验粉粹机拍击式标准振筛机、标准试验筛、HX100型试验压机。

1.3 试样制备

将杨木枝丫材和芦苇或锯或劈成小段或小片，在 55 ℃ 下真空干燥至含水率12% ～15%， 然后粉碎成-20 目(0～85 mm)的粉末备用。将杨木粉末和芦苇粉末分别倒入HX100型试验压机配备的模具内压制成条形试样。

图1为光学显微镜下2种木质粉末的颗粒形貌。不难发现，不论杨木粉末（图1a）还是芦苇粉末（图1b），其颗粒排列无序、形状各异、多为长条状。分析发现，木质粉末的松装密度随粒度的变化不大，约为绝干密度的1/2，且粒度组成成正态分布，与金属粉末的粒度分布类似[2]。

图1 木质粉末及其颗粒形貌Fig.1 Woody powder and its particle morphology

2 木质粉末冷模压成形过程的数值模拟

芦苇粉末、杨木粉末等木质粉末的成形过程是一个典型的非线性弹塑性接触问题[2,11]。MARC软件对于非线性弹塑性问题具有强大的有限元分析和计算能力，笔者将借助该软件对木质粉末在室温条件下的模压成形致密化过程进行有效模拟。

2.1 压制模型

如图2所示，基于成形模型腔横截面进行分析，取宽度50 mm，选定木质粉末粒度为-20目，假设室温为恒温25℃，装粉高度70 mm、压坯高度18 mm，成形压力分别为20、35、50、65、80 MPa，保压30 min[3-5]。取木质粉末压坯与成形模侧壁间的摩擦系数为μ=0.1，压制温度为25℃。

图2 压制模型Fig.2 Pressing model

2.2 有限元网格划分

综合考虑计算速度与精度等因素，将压制模型划分为12×10的有限元网格如图2，网格采用8节点（NODE）的平面应力（PLANE STRESS）模型。

2.3 材料模型

视木质粉末为松散各向同性体，基于等效应力和等效应变增量关系的屈服准则，拟采用粉末体本构方程（Shima-Oyane本构模型）[6]：

式中， σy为单向屈服应力；σ′ij为应力张量；P为静水压力；γ、β为材料参数（为相对密度的函数）

2.4 分析类型

采用的有限元模型是一个热机耦合模型，考虑到了弹塑性变形与接触变形等问题。在模型计算与解析时，把粉体材料定义为变形体（DEFORMABLE），把成形模具的阴模、上/下模冲定义为刚形体（RIGID）。图3所示为通过软件生成的接触表截屏图，据此建立变形体与刚形体的接触关系。

2.5 等效MISS应力云图

图4所列为-20目杨木与芦苇秆粉末在65MPa压力下成形时的等效MISS应力云图。明显可见：①粉末压坯四角应力最大，其成因在于粉末在成形过程中与模壁存在摩擦，导致压坯局部应力增大；②粉末压坯内部应力偏小、靠近阴模侧壁中部应力最小、余部应力趋于均匀，成因在于应力传递过程中粉末压坯角部摩擦使部分应力被抵消，造成压坯内部等效应力减小。

图3 接触表Fig.3 Contact table

图4 等效MISS应力Fig. 4 Equivalent MISS stress map

2.6 相对密度云图

图5 ～图7为-20目杨木与芦苇粉末在20 MPa、50 MPa、80 MPa成形压力下的压坯相对密度分布图。因侧壁摩擦力的存在，压坯密度明显成梯度分布，并呈现出一定弧线。随着保压时间的延长，粉体内部必然会发生明显的机械咬合和有限的胶接现象；成形后期，粉末压坯不同部位的密度差会缩小，但压坯芯部的密度始终低于表层密度。

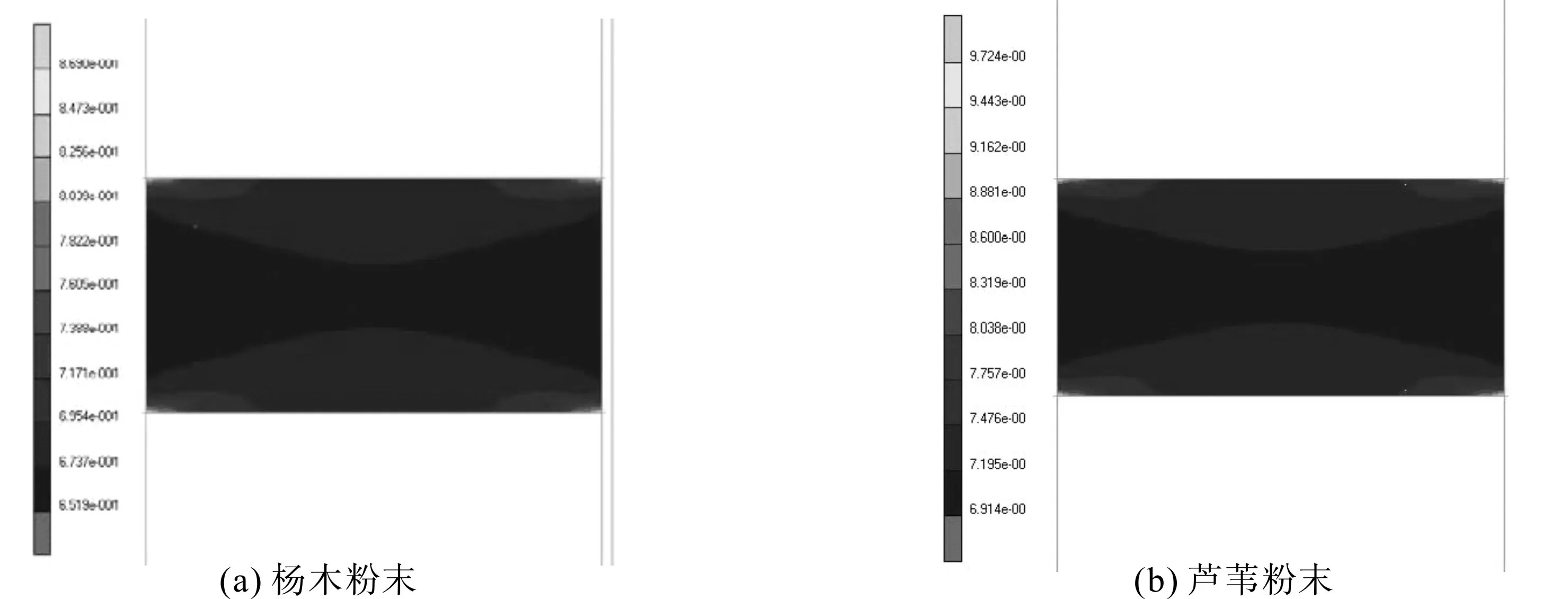
图5 20 MPa时的相对密度分布Fig. 5 Relative density pro fi le at 20 MPa

2.7 密度分析

木质粉末的常温成形过程遵循质量守恒，且压坯截面积不变，据此可根据压坯高度的变化计算出对应成形压力下的压坯密度。图8～图10展示了成形压力由0增加至80 MPa时粉末压坯的高度变化情况。

此时，压坯密度可由下式计算得出：

式中，ρ为初装密度；h0为初装高度；Δh为高度变化绝对值。

计算结果列于表1、表2。

图6 50 MPa时的相对密度分布Fig.6 Relative density pro fi le at 50 MPa

图7 80 MPa时的相对密度分布Fig.7 Relative density pro fi le at 80 MPa

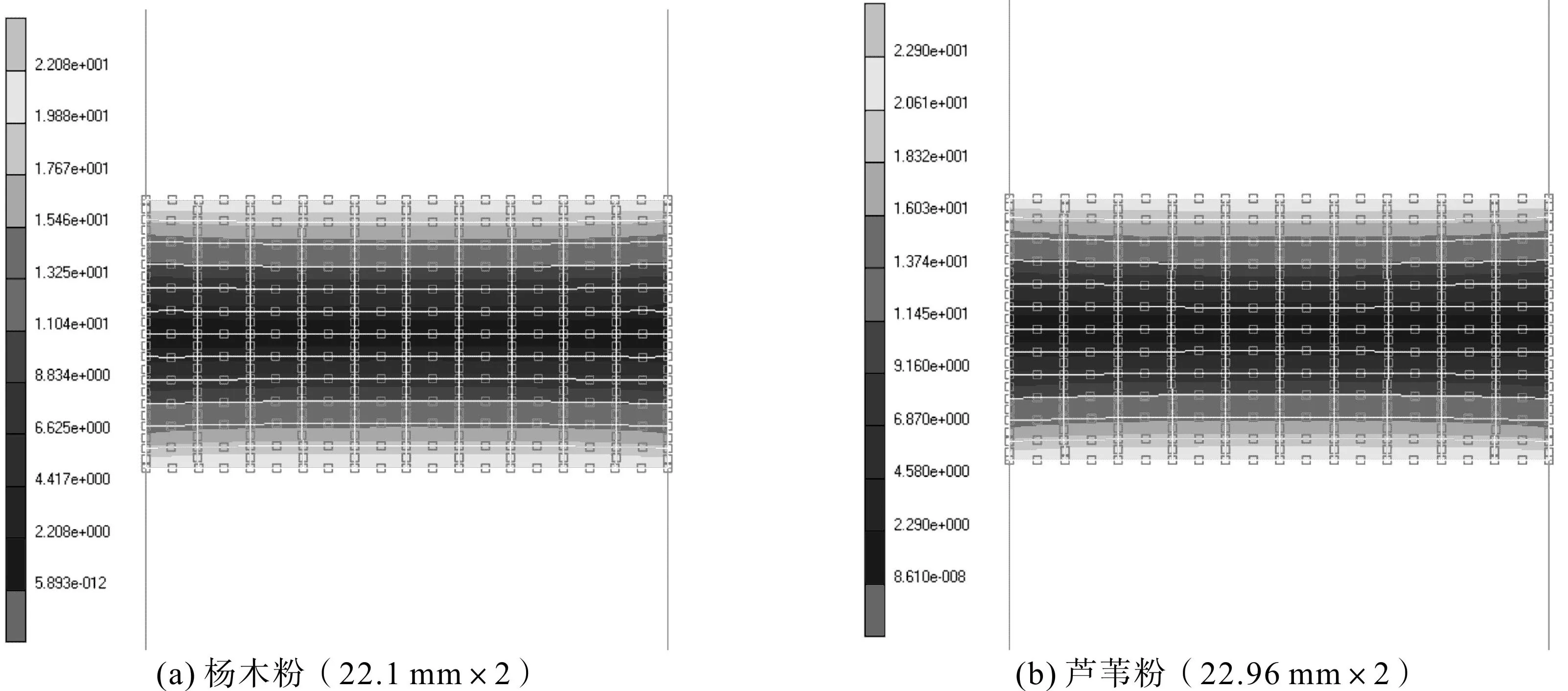
图8 20 MPa时的板坯高度变化绝对值Fig.8 Slab height change absolute value at 20MPa

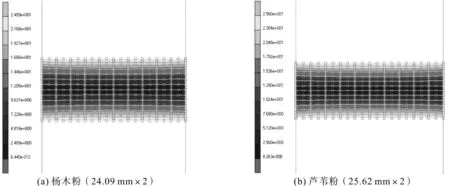
图9 50 MPa时的板坯高度变化绝对值Fig.9 Slab height change absolute value at 50MPa

图10 80 MPa时的板坯高度变化绝对值Fig.10 Slab height change absolute value at 80MPa

表1 杨木粉末压坯密度计算Table 1 Poplar powder green density calculation

表2 芦苇粉末压坯密度计算Table 2 Reed powder green density calculation

图11、图12分别为室温条件下获得的杨木粉末与芦苇粉末的压坯“压力-密度”曲线。不难发现：压坯“压力-密度”的计算曲线与实测曲线高度吻合，但也存在无规律的细微差异，其原因主要体现在2个方面：第一，在对木质粉末颗粒的理想假设中，认为颗粒体积局部保持不变，但由于木质纤维的细胞孔/壁等因素，粉末颗粒受压后实际存在一定的体积变化，而这种变化无固定规律可寻；第二，木质粉末颗粒在常温下模压成形过程中会出现较大程度的物理压缩，同时还会出现机械咬合，且压坯在成形压力撤除后会产生弹性回复。

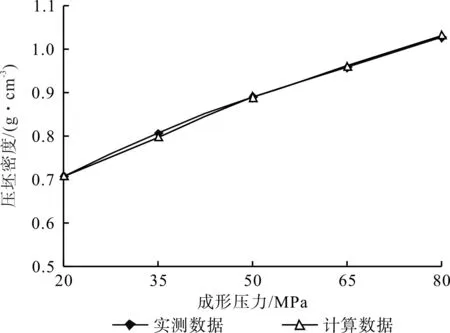
图11 杨木粉末“压力-密度”曲线Fig.11 Poplar powder pressure-density curve

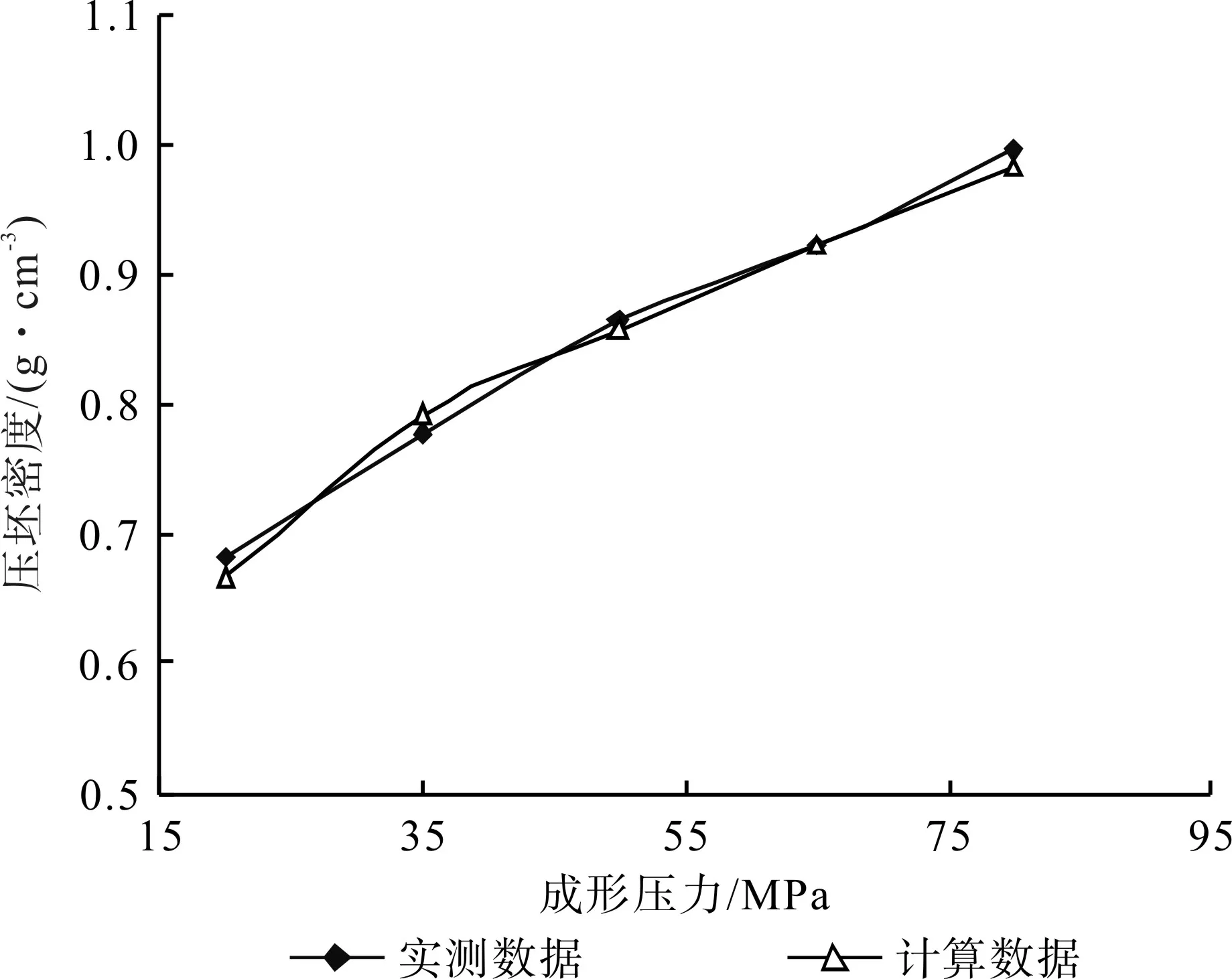
图12 芦苇粉末“压力-密度”曲线Fig.12 Reed powder pressure-density curve

3 在木质粉末热模压成形过程的应用

图13所示为粒径小于-20目杨木粉末和芦苇粉末在160℃/30 min热压条件下的“压力-密度”曲线。不难看出，当成形压力≥50 MPa时，实测压坯“压力-密度”曲线与修正“压力-密度”曲线高度一致，说明Shima模型同样适用于木质粉末热模压致密化过程数值模拟研究，木质粉末冷模压致密化过程的数值模拟研究结果对今后开展木质粉末热模压致密化过程数值模拟研究具有很好的借鉴作用。

图13 压坯密度随压力变化的数据对比Fig.13 Data comparison diagram of green density variation with pressure

4 结 论

以杨木粉末和芦苇粉末为试材，基于室温模压成形试验数据，借助有限元法分析了成形压力对木质粉末压坯密度的影响规律。结果表明：在弹塑性理论的理想假设下，Shima模型可对木质粉末冷模压成形致密化过程进行很好的数值模拟，试验结果与理论模型计算数据高度吻合，可作为木质粉末热模压成形致密化过程的数值模拟研究的基础。

初步研究发现，以杨木粉末、芦苇粉末等木质粉末为基材，在160℃/30min热压条件下的获得的模压成形压坯“压力-密度”曲线的模拟结果与实验结果存在明显偏差，但当成形压力≥50 MPa时，通过计算、实验检测与修正分析获得的压坯修正“压力-密度”曲线与实测“压力-密度”曲线基本吻合，可能的原因在于：在合适的温度区间实施热压时，木质粉末压坯的致密化机制已由粉末压缩和粉末颗粒间以及粉末颗粒内部胞壁间的融合、胶接与新官能团的形成等一系列物理化学变化，替代了冷模压时的单纯机械压缩、机械咬合和有限的粘结致密化机制，其深层次的原因与机理有待进一步研究。

[1] 李元元. 金属粉末温压成形原理与技术[M]. 广州: 华南理工大学出版社, 2008.

[2] 吴庆定. 木质粉末温压成形原理与技术[M]. 长沙: 湖南大学出版社, 2012.

[3] 吴庆定, 易 林, 梁 盛. 响应面法优化芦苇秆粉末高压无胶成形工艺[J]. 中南林业科技大学学报, 2012, 32(1): 144-149.

[4] 张 红,吴庆定,彭 博. C-stalk/Cu复合材料的温压成形与表征[J]. 中南林业科技大学学报, 2014, 34(8)：101-105.

[5] 黄 静,陈珏俐,吴庆定. 杨木粉无胶模塑成形工艺参数优化[J]. 东北林业大学学报，2012,40(2): 81-84.

[6] Kuhu H A, Downey C L. Deformation characteristics and plasticity theory of sintered powder materials[J]. International Journal of Powder Metallurgy, 1971, 7(1): 15-25.

[7] Shima S, Oyane M. Plasticity Theory for Porous Mctal[J]. Int.J.Mech. Sci., 1976, 18: 285-292.

[8] Doraicelu S M, Gegel H L, Gunasekera J S, et al. A new yield functions for compressible P/M materials[J]. International Journal of Mechanical Sciences, 1984, 26(9/10): 527-535.

[9] Kim K Y, Cho J H. A densification model for mixed metal powder under cold compaction[J]. International Journal of Mechanical Sciences, 2001, 43(12): 2929-2946.

[10] 陈火红. MARC有限元实例教程[M]. 北京:机械工业出版社,2005.

[11] 王逢瑚. 木质材料流变学[M]. 哈尔滨:东北林业大学出版社,2008.

Numerical modeling of cold-forming based on woody powder

PENG Bo, CHEN Fei, GU Liang-yao, WU Qing-ding
(Central South University of Forestry & Technology, Changsha 410004, Hunan, China)

To fi nd the densi fi cation rule of woody powder forming, used poplar powder and reed powder, and based on the experimental data of room temperature forming and the finite element method, we have analyzed the forming pressure’s impact on the rule of wood powder density. The result indicates that, under the ideal hypothesis of elastic-plastic theory, the Shima model is right down the numerical modeling of cold-forming based on woody powder densi fi cation, moreover, the experimental result is high consistent with the theoretical model calculating data. The model can be used to guide the study of hot die forming of woody powder densi fi cation.

woody powder; cold-forming; densi fi cation; numerical modeling

S781.3

A

1673-923X(2016)06-0097-06

10.14067/j.cnki.1673-923x.2016.06.020

2015-11-17

国家林业公益性行业科研专项经费资助项目（201404508）；湖南省自然科学基金/常德市联合基金资助项目（14JJ5018）；2015年湖南省重点研发计划（工业支撑计划）资助项目（2015GK3016）；湖南省研究生科研创新项目（CX2015B301）；中南林业科技大学研究生科技创新基金资助项目（CX2015B23）

彭 博，硕士研究生

吴庆定，教授，博士，博士研究生导师；E-mail：wudingle@126.com

彭 博，陈 飞，辜良瑶，等. 木质粉末冷模压成形致密化过程数值模拟[J].中南林业科技大学学报，2016,36(6):97-102.

[本文编校：吴 彬]