基于GA-BP神经网络的微裂纹漏磁定量识别技术

邱忠超， 张卫民， 张瑞蕾， 于霞， 陈国龙

(1.北京理工大学 机械与车辆学院，北京 100081；2.机械科学研究总院 先进制造技术研究中心，北京 100083；3.河北环境工程有限公司， 河北，承德 067000；4. 中国兵器工业导航与控制技术研究所，北京 100089)



基于GA-BP神经网络的微裂纹漏磁定量识别技术

邱忠超1，2， 张卫民1， 张瑞蕾3， 于霞4， 陈国龙1

(1.北京理工大学 机械与车辆学院，北京 100081；2.机械科学研究总院 先进制造技术研究中心，北京 100083；3.河北环境工程有限公司， 河北，承德 067000；4. 中国兵器工业导航与控制技术研究所，北京 100089)

针对漏磁检测定量识别技术中识别的缺陷尺寸大多为1～10 mm的较大裂纹，与实际自然裂纹相差太大的问题，将基于遗传算法优化的BP神经网络(GA-BP)算法应用到微裂纹缺陷的漏磁定量识别中，使得漏磁检测定量识别缺陷的宽度、深度达到小于0.50 mm的微细裂纹，并通过基于磁偶极子模型的理论计算与漏磁检测实验两种方法构建了微裂纹(0.10～0.30 mm)缺陷样本库. 由于在实际检测过程中存在干扰噪声的原因，实验数据的预测结果误差比理论计算数据预测结果明显偏大，最大为16.73%，但预测结果能够基本反映微裂纹缺陷的尺寸大小.

漏磁检测；遗传算法；反向传播；神经网络；微裂纹；定量识别

漏磁检测技术被广泛应用于铁磁材料的无损评估中，如油气管道、钢丝绳等[1]. 随着漏磁检测技术的发展，不仅要求对缺陷能够定性检测，而且要求对缺陷的分布情况与尺寸进行识别，即定量识别. 定量识别技术一直是漏磁检测的难点与研究热点，现已成为该技术工程应用的瓶颈问题[2].

目前对漏磁检测定量识别的研究工作主要集中在较大尺寸裂纹与仿真分析. Carvalhoa 等[3]采用BP神经网络实现了管道焊接缺陷类型的识别；Hwang等[4]提出了用径向基神经网络与径向小波基函数神经网络对人工凹坑缺陷形状重构；Ramuhalli[5]提出了一种基于神经网络和模拟退火梯度下降相结合的技术来求解反演问题;王平等[6]通过有限元仿真与实验方法实现了基于脉冲漏磁检测技术的钢轨裂纹的定量识别；张勇等[7]提出了一种基于磁偶极子模型的矩形裂纹的快速重构方法.

针对目前所识别的对象为较大尺寸裂纹(1～10 mm)，与自然裂纹相差较大的问题，并结合现有的裂纹检测标准(0.12 mm)，本文所研究的微细裂纹是指宽度与深度都小于0.50 mm的矩形裂纹. 通过基于磁偶极子模型的理论计算与漏磁检测实验两种方法构建微裂纹(0.10～0.30 mm)缺陷样本库，并将基于遗传算法优化的BP神经网络(GA-BP)应用到漏磁缺陷的定量识别中.

1 遗传算法优化BP神经网络

算法流程如图1所示[8].

BP神经网络是神经网络中应用最广的一种多层前馈神经网络，它既是前向网络的核心部分，也是神经网络的精华. 然而，BP神经网络在训练之初各层的连接权值和阈值被初始化为[0，1]间的随机值，这种未经优化的随机值会使BP神经网络的收敛速度慢，并且容易陷入局部极小值. GA-BP神经网络是用遗传算法优化BP神经网络的初始权值和阈值，其基本思想就是用个体代表网络的初始权值和阈值，个体值初始化的BP神经网络的预测误差作为该个体的适应度值，通过选择、交叉、变异操作寻找最优个体，即最优的BP神经网络初始权值和阈值.

2 漏磁样本库的建立

2.1 漏磁检测信号的获取

对垂直于试件轴线方向的裂纹进行定量识别，并采用和缺陷尺寸特征相关性较好的切向漏磁信号Hx进行研究. 通过两种途径获取切向漏磁信号，第一种为基于磁偶极子模型的理论计算，第二种为搭建漏磁检测实验系统，通过AMR磁传感器拾取漏磁检测信号. 漏磁信号随缺陷几何形状的不同而变化，而缺陷形状千差万别. 为了分析简单，实验以常见的矩形裂纹缺陷来说明漏磁信号的定量识别.

基于磁偶极子模型的理论计算是目前漏磁场分析常用的方法之一. 将裂纹类缺陷等效为无限长的矩形槽，槽宽2b，深h，P为空间中的任意一个点. 设磁化使矩形槽两侧壁均匀分布着极性相反、面密度相等的两条磁荷带，并设在槽的其它部位均无磁荷分布. 在空间任意点P(x，y)处，漏磁场的水平分量Hx表示为[2]

(1)

与磁偶极子模型不同，漏磁信号是通过AMR探头扫描含不同裂纹尺寸的16MnR钢试件得到的. 实验中，每个裂纹的长度均为10 mm，缺陷宽度、深度尺寸组合形式为(2b，h)i，单位为mm，其中，i为样本编号.

2.2 漏磁信号预处理

与磁偶极子模型得到的理想信号不同，漏磁检测实验数据是由AMR探头沿裂纹宽度方向以等空间间隔采集的[9]，信号含有较多的背景噪声，在定量化分析之前，需要对信号进行预处理. 漏磁信号预处理主要包括剔除信号奇异点，消除信号趋势项以及滤波消噪3部分，结果如图2所示.

由图2可知，信号预处理对噪声具有很强的抑制能力，不仅剔除了信号中的噪声，而且保留了原始信号中的细节.

2.3 特征量的提取

漏磁缺陷样本库如表1所示.

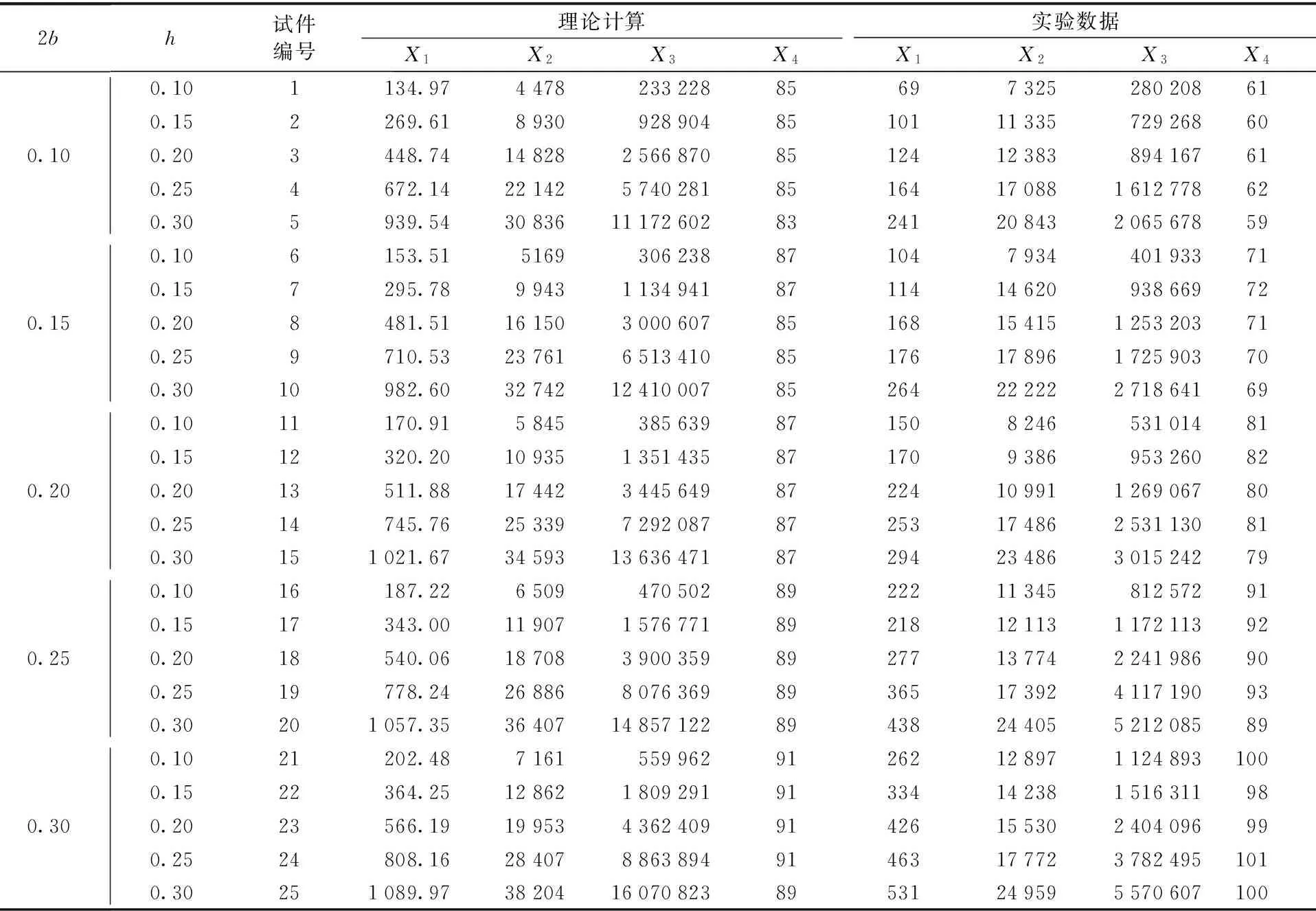
表1 漏磁缺陷样本库

漏磁信号的定量识别与其特征量密切相关，因此特征量提取是漏磁信号分析的一个关键环节. 特征提取就是利用已有的特征参数构造一个较低维数的特征空间，将原始特征中蕴含的有用信息映射到少数几个特征上，忽略多余的不相干信息.

在总结目前常见的漏磁信号特征量基础上，并考虑到实验采集到的漏磁信号含有较多噪声，定义漏磁信号的主要波形特征量如下：

① 漏磁信号波形的峰-峰值，记为X1对于漏磁场Hx，峰-峰值定义为局部异常信号的波峰与波谷幅值之差的绝对值，它是衡量裂纹深度的一个重要指标.

② 漏磁信号波形下面积，记为X2波形下面积是指一个波动中曲线波动的面积，在这里，单个缺陷的漏磁信号由峰、谷组成一个波动，它反映信号的短时一阶中心矩.

③ 漏磁信号波形的短时能量，记为X3短时能量通常指大约一个波动内的能量，它相当于信号的短时二阶原点矩，反映了在一定空间内漏磁的能量，漏磁能量增大表明此时传感器可能正处于被测试件的缺陷附件.

④ 漏磁信号波形的一次微分信号的峰-谷长值，记为X4对漏磁信号进行一次微分后，可以强化高频部分，同时反映出信号的变化率. 由漏磁场产生机理可知，在裂纹边界处漏磁信号会发生突变，故可用该特征量来衡量裂纹的宽度.

在定义了上述特征量之后，就可以利用磁偶极子模型(如式(1)所示)与检测实验得到微裂纹缺陷表面的漏磁信号，并通过特征提取构建漏磁检测样本库，见表1.

3 漏磁检测定量识别

3.1 GA-BP神经网络

BP神经网络结构包括输入层、隐含层和输出层，其中隐含层可以是一层或多层，本文所建立的BP神经网络结构为4-8-2，即输入层有4个节点(对应4个波形特征量X1～X4)，隐含层有8个节点，输出层有2个节点(对应裂纹宽度、深度)，如图3所示. 隐含层和输出层函数的选择对BP神经网络预测精度有较大影响，本文中隐含层节点转移函数选择tansig函数，输出层节点选择purelin函数. 遗传算法(GA)由遗传算法工具箱(GAOT)实现.

3.2 结果分析与讨论

为了检验特征量与算法的可靠性和实用性，对表1中的25个缺陷模型样本，选择20个作为训练数据，其余5个作为测试数据. 采用图3中所示的GA-BP神经网络对理论计算数据与实验数据进行预测，预测结果如表2所示.

由表2可以看出，理论计算数据的预测结果均达到93%以上，其中，深度的预测结果误差小于3%，宽度的预测误差稍大，最大为6.86%. 由此可知，深度与宽度的预测结果误差已达到0.01 mm级别的精度，对理论计算数据的预测结果是比较成功的.

表2 预测结果

然而，实验数据的预测结果误差比理论计算数据预测结果误差明显偏大，最大为16.73%，这是由于在实际检测过程中存在很多干扰噪声的原因，但预测结果能够基本反映缺陷的尺寸大小. 由实验数据的预测结果可知，GA-BP神经网络基本可以定量识别微裂纹缺陷的尺寸.

4 结 论

通过基于磁偶极子模型的理论计算与实验两种方法构建微裂纹缺陷样本库，并将GA-BP神经网络应用到微裂纹漏磁检测定量识别中. 结果表明：对理论计算数据，采用GA-BP神经网络预测深度与宽度的误差较小，预测结果比较成功；对实验数据，采用GA-BP神经网络基本能够定量识别人工预制微裂纹缺陷的尺寸，为自然裂纹的定量识别提供了一定基础.

[1] 黄松岭.油气管道缺陷漏磁内检测理论与应用[M].北京：机械工业出版社，2013.

Huang Songling. The theory and application of magnetic flux leakage inspection on oil-gas pipe defects[M]. Beijng: China Machine Press， 2013. (in Chinese)

[2] 王长龙，陈自立，马晓琳，等. 漏磁检测的缺陷可视化技术[M]. 北京：国防工业出版社，2014.

Wang Changlong， Chen Zili， Ma Xiaolin， et al. Visualization technology of detect in magnetic flux leakage testing[M]. Beijing: National Defense Industry Press， 2014. (in Chinese)

[3] Carvalhoa A A， Rebelloa J M A， Sagrilo L V S. MFL signals and artificial neural networks applied to detection and classification of pipe weld defects[J]. NDT&E International， 2006，39:661-667.

[4] Hwang K， Mandaym S， Udpa S S. Characterization of gas pipeline inspection signals using wavelet basis function neural networks[J]. NDT&E International， 2000，33:531-545.

[5] Ramuhalli P， Udpa L. Electromagnetic NDE signal inversion by function-approximation neural networks[J]. IEEE Transaction on Magnetics， 2002，38(6):3633-3641.

[6] Wang P， Xiong L H， Sun Y C， et al. Features extraction of sensor array based PMFL technology for detection of rail cracks[J]. Measurement， 2014，47:613-626.

[7] Zhang Y， Ye Z F， Wang C. A fast method for rectangular crack sizes reconstruction in magnetic flux leakage testing[J]. NDT&E International， 2009，42:369-375.

[8] Zhang Y X， Gao X D， Katayama S. Weld appearance prediction with BP neural network improved by genetic algorithm during disk laser welding[J]. J Manuf Syst， 2015，34:53-59.

[9] 于霞，张卫民，邱勇，等.弱磁场激励下基于阵列磁传感器的缺陷检测方法[J].北京理工大学学报，2014，34(5):460-463,469.

Yu Xia， Zhang Weimin， Qiu Yong， et al. Defect detection methods based on array magnetic sensor under weak magnetic field[J]. Transactions of Beijing Institute of Technology， 2014，34(5):460-463,469. (in Chinese)

(责任编辑：孙竹凤)

Magnetic Flux Leakage Quantitative Identification of Micro Crack Based on GA-BP Neural Network

QIU Zhong-chao1， ZHANG Wei-min1， ZHANG Rui-lei2， YU Xia3， CHEN Guo-long1

(1.School of Mechanical Engineering， Beijing Institute of Technology， Beijing 100081， China; 2.Advanced Manufacture Technology Center， China Academy of Machinery Science&Technology， Beijing 100083， China；3.Hebei Aerospace Environmental Engineering Co.， Ltd， Chengde， Hebei 067000， China; 4.Navigation and Control Technology Research Institute， China North Industries Group Corporation， Beijing 100089， China)

As the fact that the crack sizes identified based on magnetic flux leakage are larger than 1 mm generally, which are far different from the natural cracks in macro-crack check area. An algorithm with GA-BP neural network was investigated to detect quantificationally the rectangular micro-cracks with less than 0.50 mm width and depth. And a database was developed for micro crack defects among 0.10～0.30 mm based on theoretic calculation of the magnetic dipole model and experiment of magnetic flux leakage. Results show that, due to the noises interference existing in the actual detection process, the prediction error of the experimental data is larger than that of the theoretical data, and the maximum can reach 16.73%, but the prediction results can basically reflect the size of the micro cracks.

magnetic flux leakage; genetic algorithm(GA); back propagation(BP); neural network; micro crack; quantitative identification

2015-04-22

国家自然科学基金资助项目(51275048)

邱忠超(1987—)，男，博士生，E-mail：448347664@163.com.

张卫民(1964—)，男，教授，博士生导师，E-mail:Zhangwm@bit.edu.cn.

TG 115.28

A

1001-0645(2016)11-1101-05

10.15918/j.tbit1001-0645.2016.11.001