希尼尔水库灌区地下水埋深时间稳定性分析
徐继红
(新疆塔里木河流域管理局, 新疆 库尔勒 841000)
希尼尔水库灌区地下水埋深时间稳定性分析
徐继红
(新疆塔里木河流域管理局, 新疆 库尔勒 841000)
该研究基于2004—2013年对新疆希尼尔水库灌区13个观测井地下水埋深的长序列监测结果,利用相对差分法、Spearman秩相关系数法和Morlet小波变换的方法分析了研究区地下水埋深的时间稳定性和周期性特征。结果表明:在不同监测时间的地下水埋深均属于中等变异,变异系数的范围为44%~75%。地下水埋深表现出强烈的时间稳定性;小波分析表明研究区地下水埋深存在周期性变化。研究结果为灌区合理开发利用地下水资源以降低土壤盐渍化风险提供了一定的参考。
地下水; 埋深; 时间稳定性; 希尼尔水库
土壤盐渍化是由自然或人类活动引起的重要环境问题,特别是在干旱和半干旱地区。在全球范围内,每年大约有1000万hm2灌溉土地因为土壤盐渍化而荒弃。土壤盐渍化降低了土壤质量,限制了作物生长,降低了农业生产力,且在严重的情况下会导致农地弃耕。土壤盐渍化已经引起了全世界的极大关注,其分布、成因、危害及其预防措施都得到了很好的研究,一些新技术也被成功地用来识别和监测受盐渍化威胁的地区。时间稳定性的概念被定义为土壤性质的统计参数和空间位置之间不随时间变化的关联性[1]。Vachaud等最先提出了时间稳定性的概念,假设特定位置可以在一段时间内代表一个试验区的平均值[2]。其他研究人员随后的研究支持了这一假设[3]。时间稳定性的概念可以极大地降低表征野外土壤水分含量所需的样本数。鉴于土壤水分时间稳定性应用的巨大潜力,这个概念受到了极大关注。一些学者也把时间稳定性的概念应用到了土壤性质的其他方面,如Castrignanò研究了土壤电导率和钠含量的时间稳定性[4];Douaik分析了土壤盐分空间格局的时间稳定性,发现低盐点具有更好的时间稳定性,高盐点具有最弱的时间稳定性[1]。
希尼尔水库灌区是新疆尉犁县重要的农业灌区,土壤盐渍化始终是当地农业生产发展的潜在威胁。由于人类的过度开发和利用,当地的土壤盐渍化和灌溉引起的土壤次生盐渍化面积不断扩大,威胁着可持续生产和耕地保护。地下水埋深是用来确定灌区是否会引起土壤盐渍化的主要指标之一,目前为止,地下水埋深时间稳定性的相关研究鲜见报道。因此,评价地下水埋深的时间稳定性,对灌区地下水资源的监测、评价与开发具有重要意义。
1 研究区概况
希尼尔水库灌区属温带大陆性干旱气候区,多年平均气温为11.5℃,多年平均降雨量为55mm,多年平均蒸发量为2150mm,年均地下水埋深为3~10m。灌区地下水补给来源主要是引水灌溉,地面20~30m以下的古湖沉积物中富集了大量的可溶盐类,在水循环作用下,古湖沉积物中富集的可溶盐上升,致使潜水矿化度偏高,有些地区水味咸苦,不能引灌。目前,灌区种植的主要是小麦、红枣、棉花、蔬菜等作物。
2 研究方法
2004—2013年对希尼尔灌区13个观测井的地下水埋深特征进行监测分析。
2.1 分析方法
两种方法被用来检验地下水埋深的时间稳定性:相对差分法和Spearman秩相关系数法[2]。对于相对差分法,相对差分δij是基于测量点i(i=1,…,13)在时间j(j=1,…,10)的地下水埋深与时间j的所有测量值的均值的差,即
(1)
相对差分在时间上的均值(mean relative difference,MRD),即平均相对差分和标准差(standard deviation of relative difference,SDRD)的计算公式分别为
(2)
(3)
式中m——测量的次数。
所有测量点按照MRD由小到大的顺序排列起来,并标注出每一个样点的SDRD。小的MRD值表示位置点有时间稳定性,大的MRD值表示位置点存在强的时间变异性。根据Vachaud等的结论,如果一个样点的MRD接近于零并且SDRD也比较小,那么这个点就是代表性位置点。位置点MRD值在±0.05范围内可以被认为是接近于0[5]。样点的MRD值在±0.05之间变化是预测研究区地下水平均埋深状况的一个必要条件,时间稳定性位置点要满足的另一个条件是SDRD值较小。
第二种方法是基于非参数Spearman秩相关系数rs:
(4)
式中Rij——在位置点i和时间j观测值的秩;
Rik——观测值在同一个位置点i而不同时间k的秩;
n——观测点总数。
所有观测点在不同测量时间的这种相关性均被计算。rs是一个介于-1和+1之间的变量,rs值越接近于1说明时间稳定性越好,越接近于0说明时间稳定性越差。
不同时间尺度下的地下水埋深的周期性采用Morlet小波变换分析[6]。
3 结果与分析
3.1 地下水埋深的时间变化特征
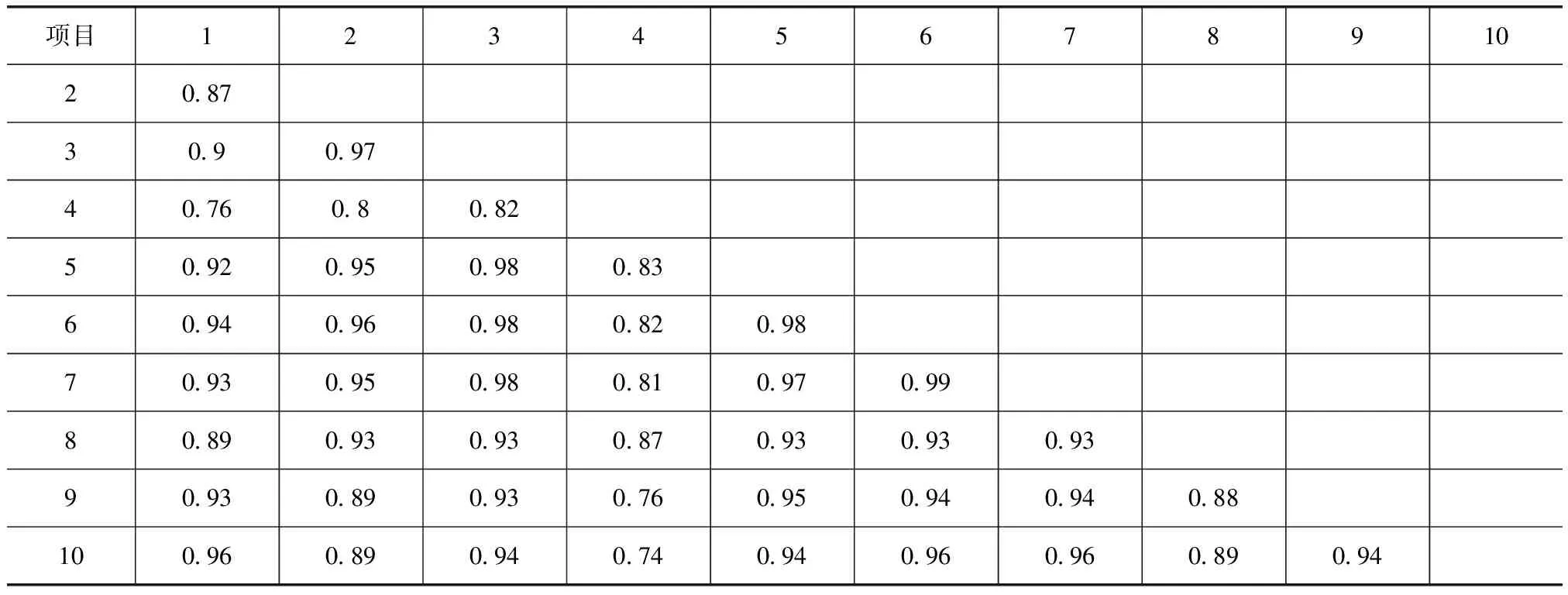
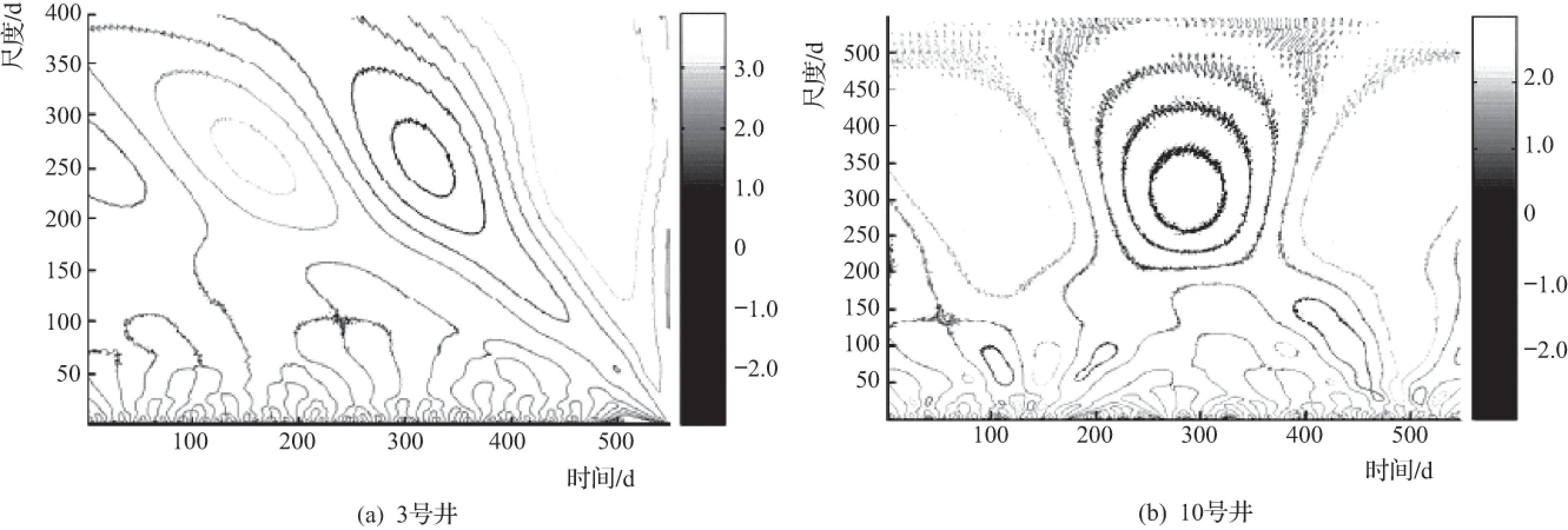
2004—2013年10个时间点下不同观测井点地下水埋深的统计特征见表1。变异系数(coefficient of variation,CV)可以用来定量确定空间变异的程度:弱变异CV≤10%,中等变异10% 3.2 地下水埋深的时间稳定性分析 Spearman秩相关系数法是一个可以表达同一变量在不同时间变化强度和方向的非参数检验方法[1],主要反映测量样点空间模式在时间上的相似性。井点地下水埋深在10个时间点的Spearman秩相关系数(rs)见表2。由表2可见,rs变化范围为0.74~0.99,其值均在P<0.01水平极显著相关且大部分rs值均接近于1,这说明研究区地下水埋深表现出强烈的时间稳定性。 表1 不同时间观测井地下水埋深统计特征 表2 不同时间点的地下水埋深Spearman秩相关系数 3.3 地下水埋深的周期性 基于小波变换分析了研究区地下水埋深的周期性,2008年3月—2009年3月研究区典型井点(3号井与10号井)的地下水水位距平值Morlet小波变换见下页图。小波系数的大小代表了信号强弱。等值线颜色越浅,小波系数值越高,埋深值越大,反之则小波系数值越低。在200d之前,3号井的地下水埋深在120d尺度振动明显;在200d之后,其在200d尺度振动明显。地下水埋深振动周期随着时间的推移逐渐变大。2008年3月—2008年9月期间,地下水埋深振动周期小,埋深变化较快;2008年9月—2009年9月期间,埋深振动周期大,埋深变化相对缓慢。根据地下水埋深小波系数求得相应尺度的小波方差,结果有3个峰值,分别对应于时间尺度90d、200d和310d。地下水水位最明显的振动周期为250d,小波方差峰值对应的时间尺度为60d和300d。10号井地下水埋深在300d尺度振动明显,小波方差有3个峰值,分别对应于时间尺度60d、90d和280d。地下水水位最明显的振动周期为300d,小波方差峰值对应的时间尺度为60d、90d和360d。因此,3号井和10号井的地下水埋深在不同的时间尺度下均呈现出不同的周期性。 不同时间尺度下的地下水埋深距平小波变换图 a.希尼尔水库灌区地下水埋深在不同监测时间均属于中等变异,其变异系数CV的范围为0.64~0.75。 b.研究区地下水埋深数据的秩相关系数rs变化范围为0.74~0.99,其值均在P<0.01水平极显著相关且大部分rs值均接近于1,地下水埋深具有强烈的时间稳定性。 c.基于对研究区3号井和10号井地下水埋深的小波分析,表明研究区地下水埋深存在不同时间尺度下的周期性变化。 [1] Douaik A.Temporal stability of spatial patterns of soil salinity determined from laboratory and field electrolytic conductivity[J]. Arid Land Research and Management, 2006(20): 1-13. [2] Vachaud G, De Silans A P, Balabanis P. Temporal stability of spatially measured soil water probability density function[J]. Soil Science Society of America Journal, 1985,49(4): 822-828. [3] Grayson R B, Western A W. Towards areal estimation of soil water content from point measurements: time and space stability of mean response[J]. Journal of Hydrology, 1998, 207(1/2): 68-82. [4] Castrignano A, Lopez G. Temporal and spatial variability of electrolytic conductivity, Na content and sodium adsorption ratio of saturation extract measurements[J]. European Journal of Agronomy,1993,3(3):221-226. [5] Gao L, Shao M A. Temporal stability of shallow soil water content for three adjacent transects on a hillslope[J]. Agricultural Water Management, 2012(110): 41-54. [6] Grossman A, Morlet J. Decomposition of Hardy functions into square integrable wavelets of constant shape[J]. SIAM J. Math. Anal., 1984, 15(4): 723-736. [7] Nielsen D R, Bouma J. Soil spatial variability[M]. Pudoc:Wageningen, 1985. Analysis on groundwater buried depth time stability in Xinier Reservoir irrigation district XU Jihong (Xinjiang Tarim River Basin Administration, Korla 841000, China) The research is based on long series monitoring results of 13 observation well groundwater buried depth in Xinjiang Xinier Reservoir irrigation district from 2004 to 2013. Relative difference method, Spearman rank correlation coefficient method and Morlet wavelet transform method are utilized to analyze the time stability and periodic characteristics of groundwater buried depth in the study area. The results show that the buried depth of groundwater in different monitoring time belongs to medium variation. The range of variation coefficient is 44%~75%. Groundwater buried depth shows strong time stability. Wavelet analysis shows that the embedded depth of groundwater in the study area has cyclical change. The results of the study provide certain reference for reasonable exploitation and utilization of groundwater resources and reduce soil salinization risk in the irrigation district. groundwater; buried depth; time stability; Xinier Reservoir 10.16616/j.cnki.10-1326/TV.2016.07.020 TV213.4 B 2096- 0131(2016)07- 0070- 04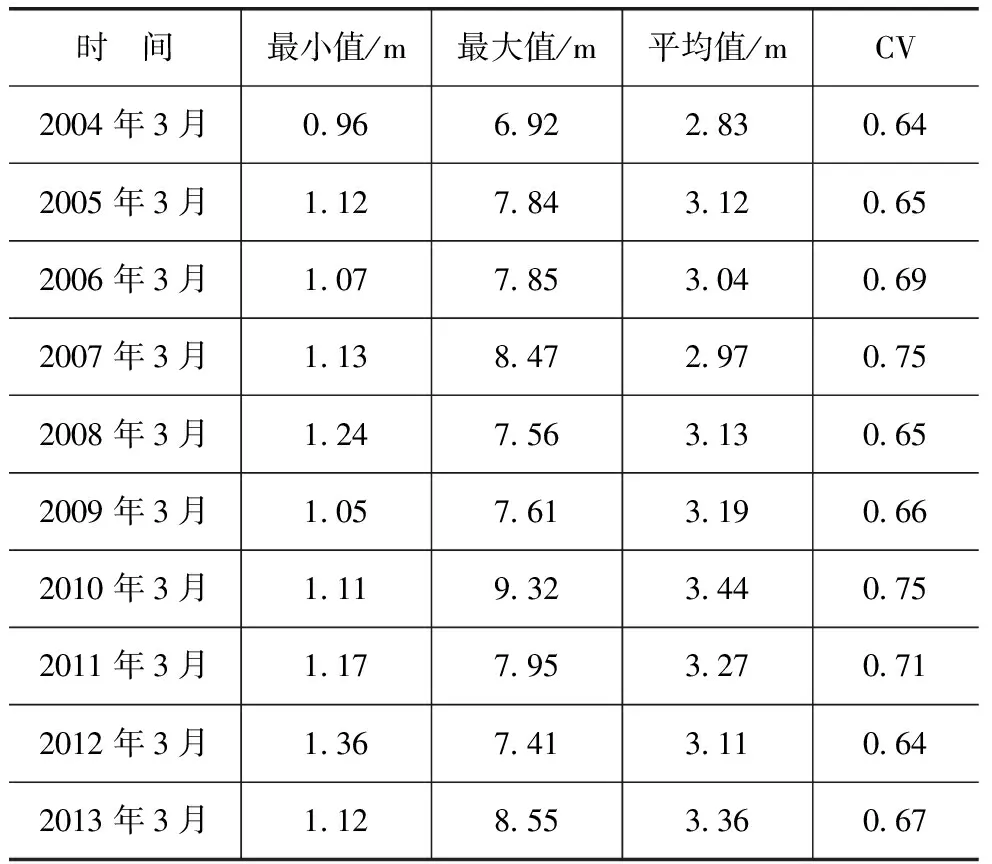
4 结 语

