关于立体几何线面平行问题的解题方法

陕西省西安高新唐南中学 (710065)

蒋金雨●



关于立体几何线面平行问题的解题方法

陕西省西安高新唐南中学 (710065)

蒋金雨●

对于立体几何而言，如何有效地使用解题方法成为了我们主要关注的问题.立体几何问题是一种抽象化的问题，而且其中线面平行的问题更是高考的热点问题.对于线面平行，其核心内容便是依据相关的定理和概念，加之对平行关系的应用，进而做好线面平行问题的解析.

一、空间几何思想解决立体几何中的线面平行问题

高中数学立体几何中线面平行问题的解答过程中，要对立体几何中线和面平行的相关知识进行全面的分析，并且要熟练地应用在分析题目中，进而快速而熟练地解决问题.

对于空间几何图形平行的关系而言，不仅有线线平行，线面平行，还有面面平行，而本文主要研究线面平行.主要使用的定理如下所示：

若平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行.可以表示为：若直线l⊄α，直线b⊆α，l∥b，则l∥α.

二、利用平行四边形思想解决立体几何中线面平行问题

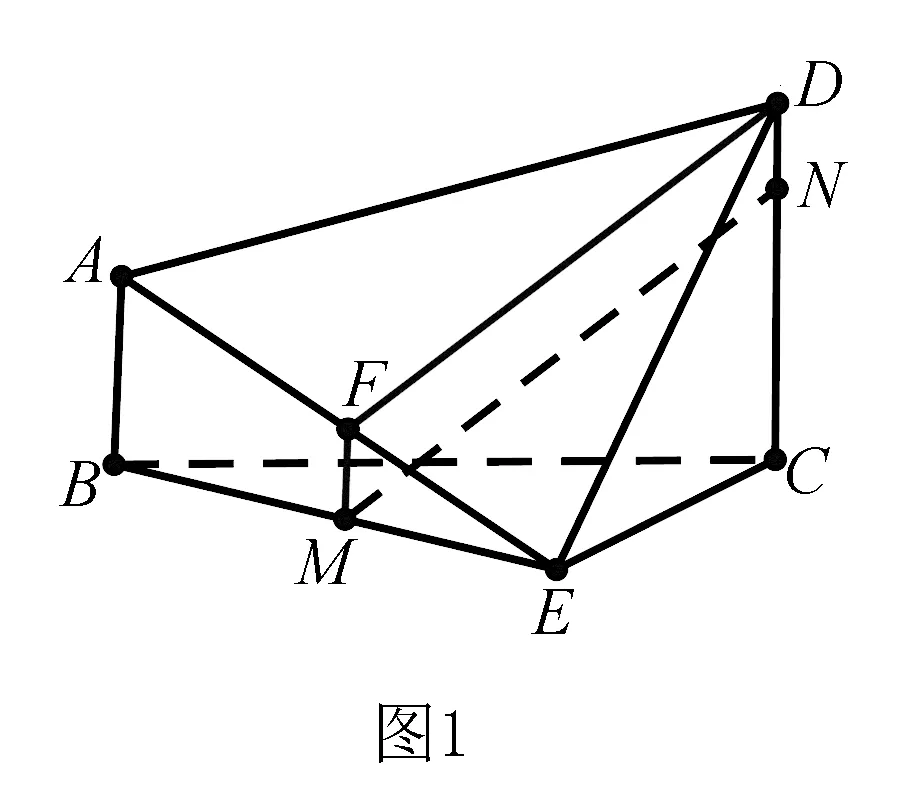
证明 取AE中点F.

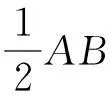
这种类型的题便是利用几何体的空间结构和性质，巧妙地利用辅助线，进而对立体几何中的线面平行问题进行解决.

三、利用比例关系解决立体几何中线面平行的问题

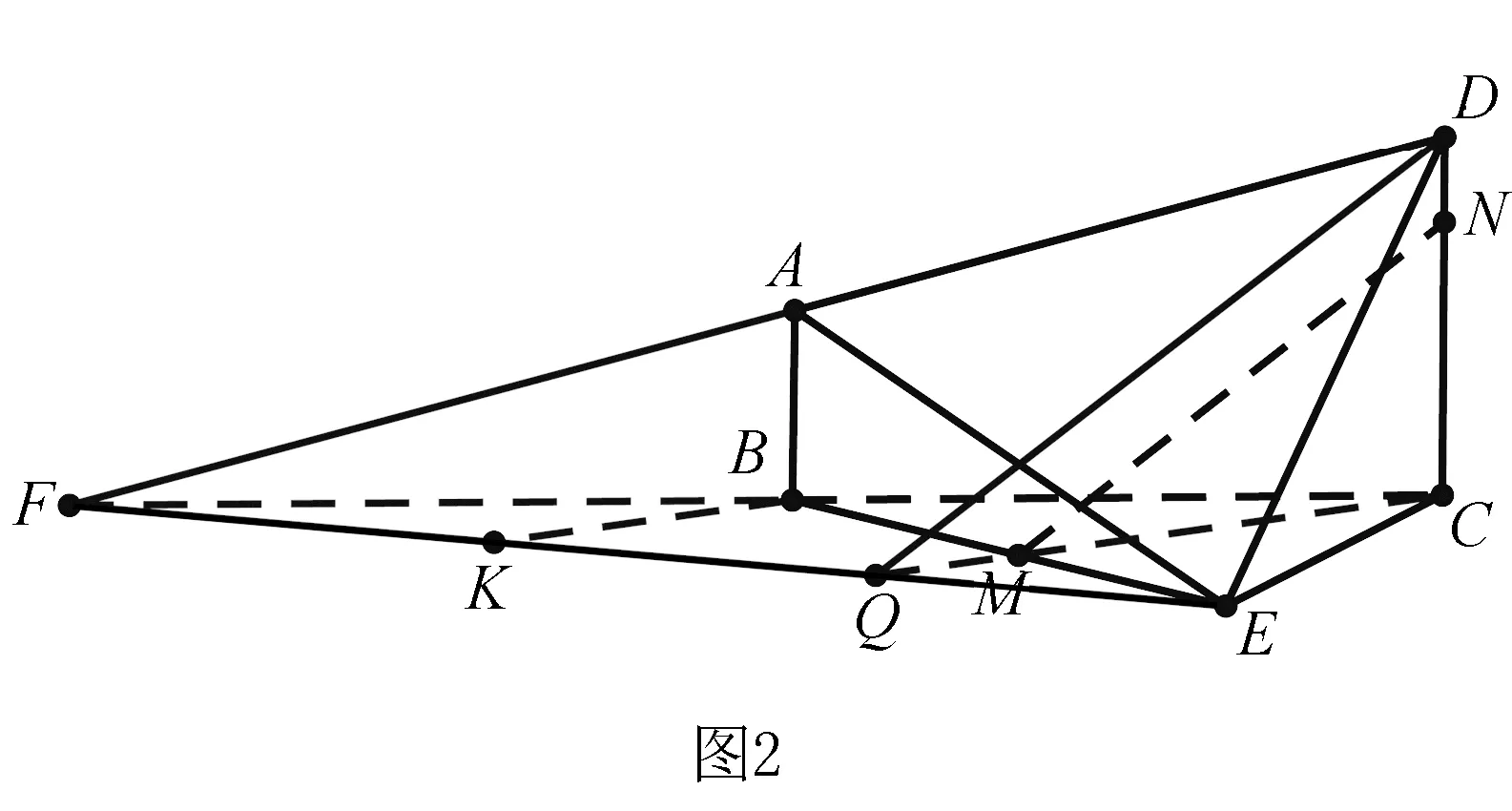
在这道题的求解过程中，首先我们在题目中已经知道比例关系，为了利用比例关系，所以我们构造辅助线利用其中的比例关系来解答这道题.因为比例关系只能应用到一个平面内，所以我们要把已知的比例关系转化到平面内可以利用的比例关系，于是我们将平面ADE扩大到平面FDE，构造出DN，NC的比例关系，证明如下，

证明 延长DA、CB交于点F，连接CM并延长交EF于点Q，过点B作MQ的平行线BK.

∵M是BE的中点,

∴Q是KE的中点.

在△FQC中，BK是中位线,

可得K是EF的三等分点,

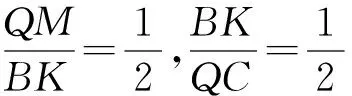
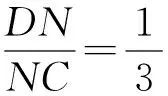
∵DQ⊆平面ADE，MN⊄平面ADE

∴MN∥平面ADE.但是，需要注意的是，有时，题目没给比例，但隐含比例，要善于挖掘比例.例如，在高中数学中的这一例题而言，如图3已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一平面内，P、Q分别是对角线AE、BD上的点，且AP=DQ.

求证：PQ∥平面CBE.

在这道题中，虽然没有直接告诉我们比例关系，但我们通过读题可以挖掘出两个矩形中所蕴含的比例关系.

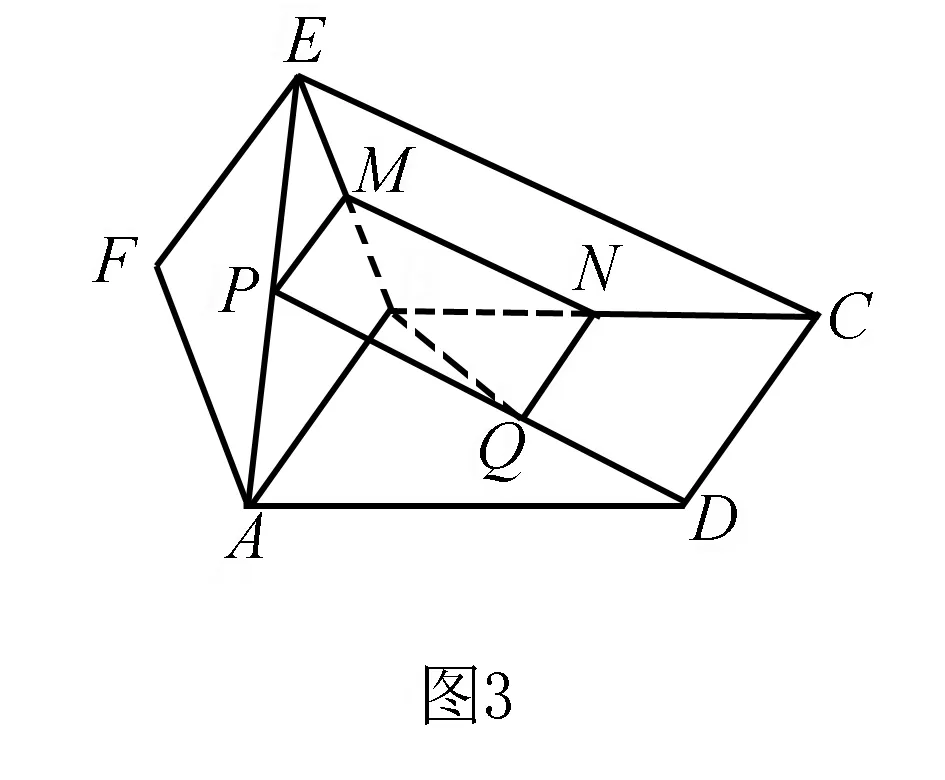
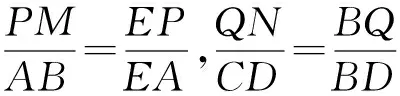
∵AP=DQ,

∴EP=BQ.

又AB=CD,EA=BD,

∴PM=QN.又PM∥QN，∴四边形PMNQ是平行四边形，

∴PQ∥MN.

∵PQ⊄平面CBE，MN⊂平面CBE，

∴PQ∥平面CBE.

四、中位线定理解决立体几何中的线面平行问题

高中数学里，中位线定理是我们十分常用的定理，不管是在平面几何，还是立体几何中中位线定理都有极为广泛的应用.当然，在立体几何中，我们必须把线段转化在同一平面内才可以继续使用，因为中位线定理只可以研究平面中线段问题.其实，使用中位线定理便是利用面面平行在逆推出线面平行.其中面面平行所使用的定理如下所示：如果一个平面内有两条相交直线与另一个平面平行，那么这两个平面平行.几何语言：a⊂α，b⊂α，且a∩b=A，a∥β，b∥β，则α∥β.

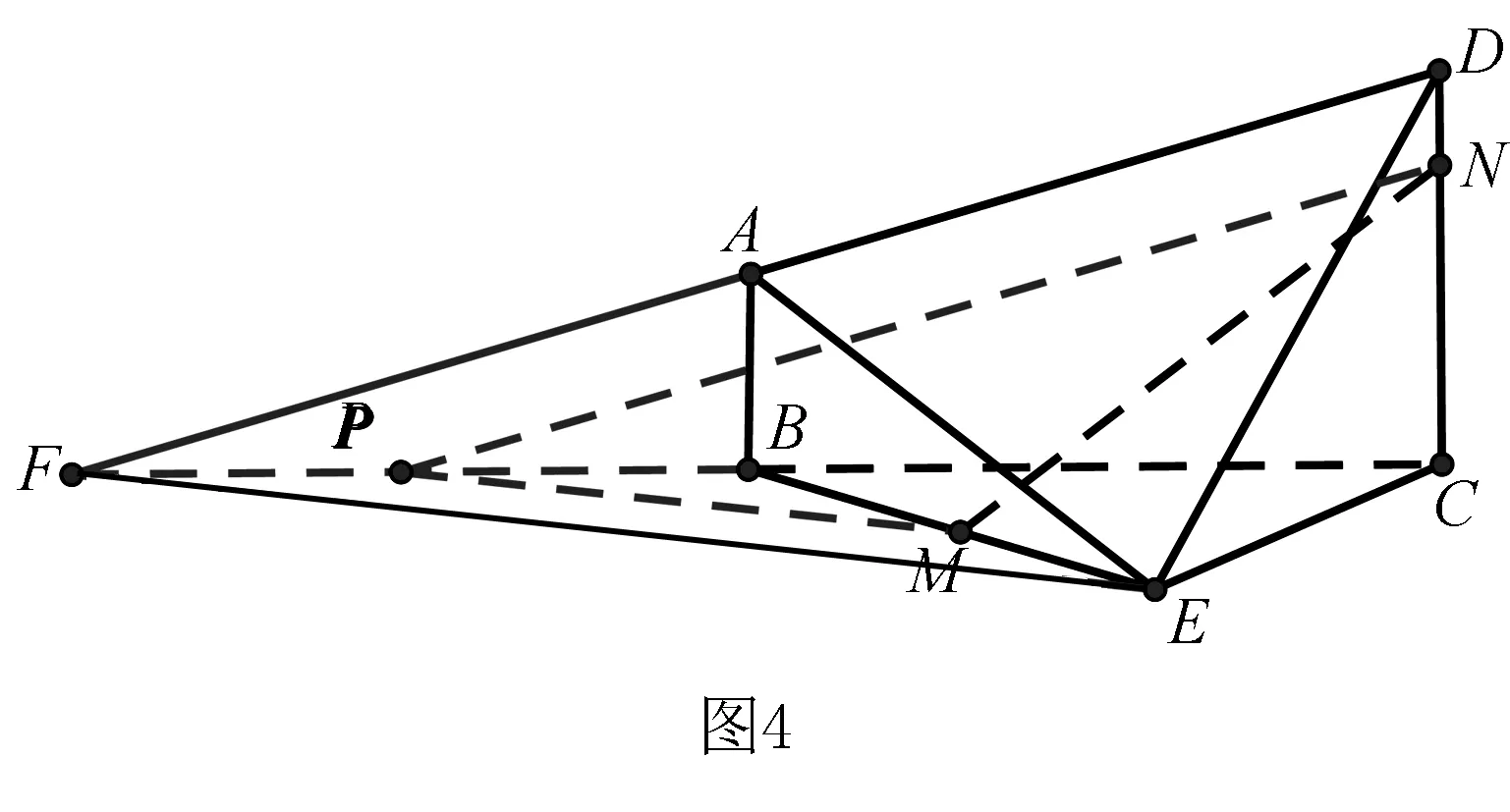
求证：MN∥平面ADE.

在这道题中，我们先确定出要使用中位线定理，于是我们延长DA，CB交于点F，过点M作MP∥EF，再连接NP,于是便构造出了平面FDE与平面PMN平行，通过面面平行，再结合中位线定理，便可以推出MN∥平面ADE.证明如下.

证明 延长DA，CB交于点F，过点M作MP∥EF，再连接NP.

∵M是BE的中点,

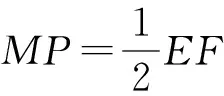
∴P是FC是四等分点.

∵DF∩EF=F，NP∩MP=P.

∴平面NPM∥平面DFE.

∵MN⊂平面NPM，MN⊄平面ADE,

∴MN∥平面ADE.

终上所述，本文通过同一道题介绍了立体几何中线面平行的三种解题方法：利用平行四边形的性质解题；利用比例关系解题；利用中位线定理和面面平行定理相结合解题.一题多解拓宽了我们解题的思路，当然数学的学习讲究融会贯通，将相关的旧知识同新知识联系在一起.做几何题，培养灵活思维，运用多种方法可以帮助我们更快地解决问题.

G632

B

1008-0333(2016)31-0037-02