函数型非参数回归模型及其在金融中的应用

王咪咪；丁 辉



函数型非参数回归模型及其在金融中的应用

王咪咪；丁 辉

函数型数据分析是分析高频数据的重要工具。在实际中函数型协变量和响应变量之间的线性假设通常不成立。本文提出了函数型非参数部分自回归模型来刻画函数型协变量和响应变量之间的非线性关系，本文接着使用非参数核估计方法给出了该模型的估计，并通过统计模拟验证了该估计方法的优良性，最后我们给出了上证指数的一个实例来说明我们模型的良好预测能力。

函数型数据；高频数据；非参数回归模型；核估计

随着科技的发展，人们收集数据的技术和手段越来越先进，这就使得我们在经济金融领域中往往能收集到一些段时间内连续的观测数据。例如，在金融交易市场上，在交易日的交易时段内随时都有交易，都会产生交易数据，即连续时间段内的高频数据。这些高频数据明显具有函数型数据的特征，因此把他们看成函数型数据，利用函数型数据分析是高效地处理和利用这些高频交易数据的一个有效的手段和方法。

函数型数据分析方法已经广泛地应用在生物学、计量化学、心理学、地理学、气象学、经济学和金融学等等领域。到目前为止，国内外已经有不少利用函数型数据分析方法研究金融市场中的内在规律的研究成果。例如：程丽娟[4]通过函数型部分线性回归模型研究了上证指数的预测问题；姜高霞和王文剑[5]通过建立函数型时序分解模型研究了CPI的经济周期问题；蔺顺峰[6]通过使用函数型聚类分析方法研究了我国副省级城市年平均工资差异问题；龙文等[7]通过使用函数型主成分分析方法研究了不同国家金融危机中经济发展的差异性问题；田华平[9]通过使用函数型聚类方法研究了中国股市量价关系问题。但是上述研究成果凡是借助于函数型数据回归模型讨论的都有一个基本假设：函数型协变量与响应变量之间满足线性关系。但是，在实际中，这种假设不一定成立。因此，本文利用函数型非参数回归模型来刻画函数型协变量和响应变量之间的关系，该模型比上述模型更灵活，更具有广泛的适用性。

文章的大致结构如下：第一部分介绍函数型数据分析在金融领域内的研究现状；第二部分引入函数型非参数回归模型，并阐述该模型的估计与优点；第三部分介绍该模型的统计模拟，说明该估计方法的有效性；第四部分介绍该模型在金融上证指数上的应用。第五部分是总结和展望。

1 函数型非参数回归模型

函数型非参数回归模型的形式如下：

(1)

其中X(t)是定义在区间I上平方可积的函数型协变量且可完全观测，g(·)是从平方可积空间到实数域上的实值函数，即g:L2→R，Y是标量型响应变量，ε是误差项且满足Eε=0,Varε=σ2。该模型具有很广泛的适用性和灵活性，且该模型脱离了函数型协变量和标量型响应变量的线性束缚，且函数型线性模型是该模型的一个特例(即：g(X(t))=∫IX(t)β(t)dt)。

关于该模型的估计，我们采用非参数Nadaraya-Watson核估计[1]，可得

(2)

其中

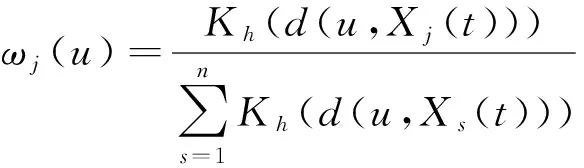
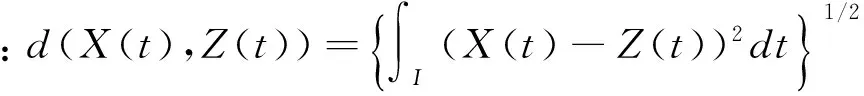
到此为止，我们已经得到了该模型的估计。当然，在模型的估计过程中涉及到窗宽参数h的选取，关于窗宽参数h的选择有很多准则，例如交叉核实，GCV准则，AIC准则和BIC准则等等，我们在进行估计的时候采取交叉核实准则，即最小化下面式子：

函数型非参数回归模型由于脱离了函数型协变量和标量型响应变量的线性束缚，因此模型本身具有更大的灵活性和适用性。

2 统计模拟

为了说明模型估计的有效性，我们进行统计模拟。我们按照下面的模型来生成数据：

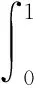
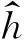
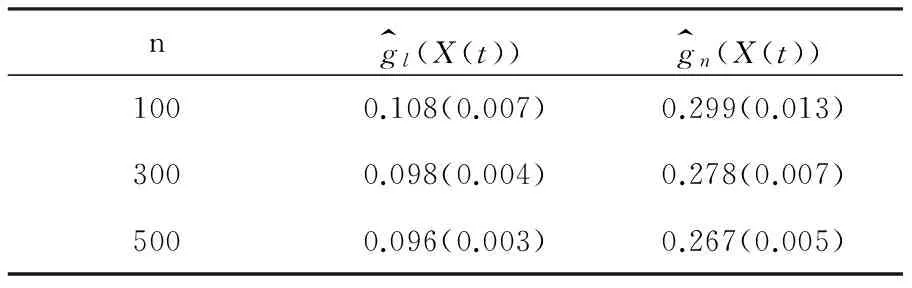
表1 在第一种情形下RASEs和标准差(括号里)结果表

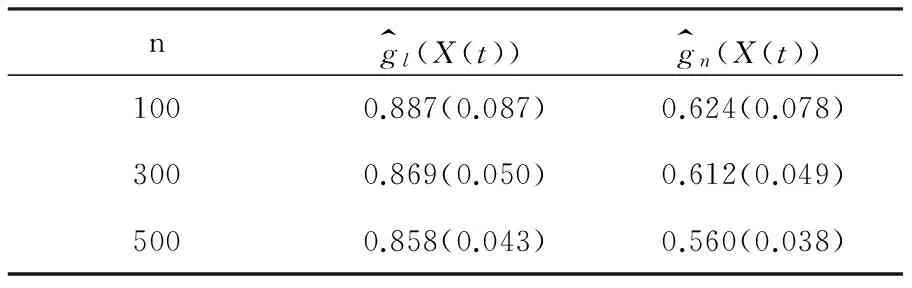
表2 在第二种情形下RASEs和标准差(括号里)结果表

由表1和表2可以看出，非参数g(X(t))估计均方误RASE随着样本量的增加而减少。在模型为函数型线性模型的情况下，采用线性模型的估计效果较好，但是用函数型非参数回归模型估计，估计的均方误结果在0.3左右，是可以接受的。但是在第二种情况下，本身模型不是线性模型，如果采用采用线性模型的方法估计，则均方误就会变大很多，基本上在0.9左右，而用非参数方法估计均方误相对小的多，大概在0.6左右，约少了33%。因此通过统计模拟可以说明我们的函数型非参数回归的估计方法是有效的。

3 实证分析

在这部分，我们将把函数型非参数回归模型用到上证指数数据中来说明我们模型的优点。我们选取2015年6月1日到2016年3月1日共183个交易日的上证指数数据。该数据包含上证指数开盘价Y，及其每个交易日每5分钟的上证指数价格X(t)，其中由于每个交易日的交易时间为9:30-11:30及13:00-15:00，因此每个交易日每五分钟的上证指数数据共48个。我们首先对数据进行预处理，对上证指数当天开盘价除以上一天的开盘价，即开盘比率作为Yi，我们的目标是找出合适的模型对上证指数开盘价进行预测。因此我们需要找出开盘价格Yi与每5分钟的上证指数价格Xi(t)之间的关系，由于上证指数开盘比率Yi与每5分钟的上证指数价格Xi(t)之间不一定满足线性关系，因此我们考虑利用函数型非参数回归模型来刻画找出开盘比率Yi与每5分钟的上证指数价格Xi(t)的关系，即

(3)

为了比较不同模型对上证指数开盘价格的预测能力，我们考虑两种不同的模型：函数型线性模型和函数型非参数回归模型。为了考察模型的预测效果，我们采用滚动预测法：从前163个数据作为训练集开始，预测第164个数据，然后再把前164 个数据作为训练集，预测第165个数据，……，直到我们将前182个数据作为训练集，预测第183个数据为止。我们采用的对不同模型的预测好坏的比较准则是：平均预测误差

不同模型及其相对应的平均预测误差结果如下表4-1：

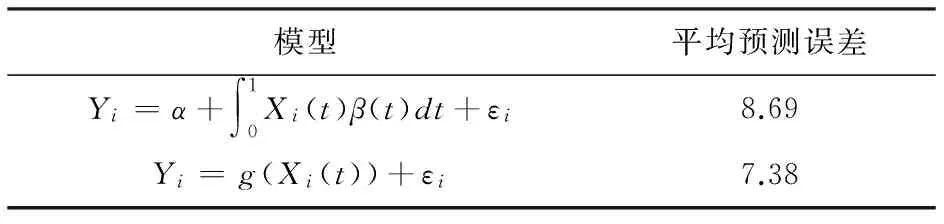
表4 不同模型及其相对应的平均预测误差(单位×10-4)

从表4可以看出我们的函数型非参数回归模型的平均预测误差较小，比线性模型预测效果提高了15%。因此在这两个模型中函数型非参数回归模型的预测效果较好，该模型可以为我们今后处理金融中高频数据提供一个新的思路。

4 总结

函数型非参数回归模型克服了函数型协变量与响应变量之间满足线性关系的约束，并且该模型是函数型线性模型的推广，因此该模型具有很大的灵活性和适用性。该模型可以为我们研究金融市场中的高频数据和函数型数据提供一种新的模式。

[1] Eubank, R.L. Nonparametric regression and spline smoothing [M].New York: Marcel Dekker Inc, 1999:155-216.

[2] Fan, J. and Gijbels, I. Local polynomial modelling and its application [M]. London: Chapman and Hall, 1996: 13-56.

[3] Ramsay, J. O. and Silverman B. W. Functional Data Analysis [M]. New York: Springer, 1997:17-79.

[4] 程丽娟. 基于部分函数型线性回归模型的上证指数预测[J]. 泰山学院学报, 2016, 38(3): 14-17.

[5] 姜高霞, 王文剑. 经济周期波动的函数型时序分解方法——基于CPI的实证分析[J]. 统计与信息论坛, 2014, 29(3):22-28.

[6] 蔺顺锋, 易丹辉, 肖宏伟. 基于函数型数据分析视角的我国副省级城市年平均工资差异研究[J]. 现代管理科学, 2015(3):27-29.

[7] 龙文, 李楠, 王惠文, 成思危. 金融危机过程中不同类型国家经济发展的差异性比较——基于函数数据分析方法[J]. 管理评论, 2014, 26(3):3-10.

[8] 米子川, 赵丽琴. 函数型数据分析的研究进展和技术框架[J]. 统计与信息论坛, 2012, 27(6):13-20.

[9] 田华平. 基于函数型数据聚类分析方法的中国股市价量关系研究[J]. 时代金融旬刊, 2013(3):26-29.

[10] 赵煜, 秦增举. 函数型数据分析及其在生态经济系统中的应用展望[J]. 甘肃科技, 2015, 31(16):66-68.

责任编辑：王 与

Functional Nonparametric Regression Model and its Applications in Finance

Wang Mimi，Ding Hui

Functional data analysis is the important tool of analysis high frequency data. The linear assumption between functional covariate and response variable are usually false in practice. This paper propose functional nonparametric partial auto-regression model to model the nonlinear relation of functional covariate and response variable. Nonparametric kernel estimation is used to obtain the estimators of model. We conduct simulation to show that our method have excellent performance. A real data example about shanghai stock index data is used to illustrate our model have good prediction ability.

Functional data；high frequency data；Partial nonparametric regression model；kernel estimation

O212.7

A

1673-1794(2016)05-0018-03

王咪咪，滁州学院数学与金融学院讲师，硕士；丁辉，滁州学院数学与金融学院讲师，硕士(安徽 滁州 239000)。

全国统计科学研究计划项目( 2012LY153) ; 滁州学院科研启动基金资助项目( 2014qd012) ;安徽省自然科学基金研究项目( KJ2014A180);安徽省金融工程教学团队(2013jxtd035)

2016-07-21