2-距离空间中Fisher型映象的公共不动点定理

赵美娜, 张树义, 郑晓迪

(1.渤海大学数理学院,辽宁 锦州 121013; 2.锦州师范高等专科学校,辽宁 锦州 121001)



2-距离空间中Fisher型映象的公共不动点定理

赵美娜1, 张树义1, 郑晓迪2

(1.渤海大学数理学院,辽宁 锦州 121013; 2.锦州师范高等专科学校,辽宁 锦州 121001)

使用广义拟弱交换概念, 在完备2-距离空间中研究了涉及四个映象的Fisher型压缩映象公共不动点的存在性和唯一性, 证明了新的公共不动点定理, 从而改进和推广了现有文献中的相应结果.

完备2-距离空间;Fisher型映象;广义拟弱交换;公共不动点

Fisher[1]在完备度量空间(X,d)上研究了两个自映象S和T满足如下条件的不动点的存在性：

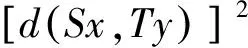
曾文智[2]推广了文[1]中的结果,研究了下列Fisher型映象S和T的不动点的存在性：

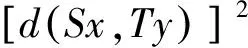
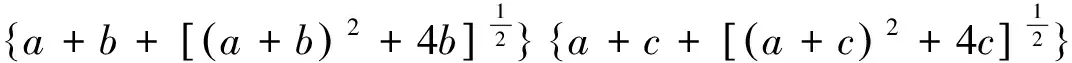
张树义[3]使用广义拟弱交换概念,研究了下列涉及四个自映象的Fisher型映象的公共不动点的存在性,从而推广了文献[1-2]中的结果:

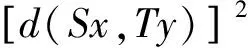
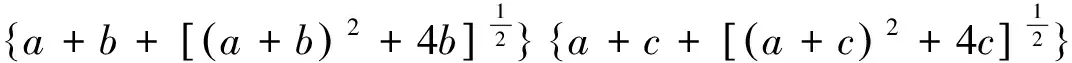
近些年来, 文[4-14]研究了一些非线性映象不动点的存在性. 受上述工作启发,本文在2-距离空间中研究Fisher型映象不动点的存在性, 所得结果改进和推广了有关文献中的相应结果.

1 预备知识

定义1 (X,d)称为2-距离空间,如果X是一空间,d是定义在X×X×X上满足下述条件的一非负实值函数：

1)对每一对点a,b∈X,a≠b存在一点c∈X,使得d(a,b,c)≠0；

2)d(a,b,c)=0,当a,b,c中至少有二元相等；

3)d(a,b,c)=d(a,c,b)=d(b,c,a)；

4)d(a,b,c)≤d(a,b,x)+d(a,x,c)+d(x,b,c),其中x是X中的任一元.

条件4)称为三角形面积不等式.

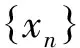
2-距离空间(X,d)称为完备的,若X中的每一Cauchy列都是X中的收敛列.

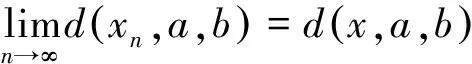
定义3[4]2-距离空间(X,d)中自映象T和J称为广义拟弱交换,如果存在φ:R+→R+=[0,+∞),在R+连续且φ(0)=0,使得对一切x,a∈X,有d(TJx,JTx,a)≤φ(d(Tx,Jx,a)).

2 主要结果

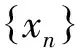
有

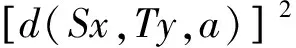
cd(By,Sx,a)d(By,Ty,a)+λd(Ax,Ty,a)d(By,Sx,a),

(1)

证明 令y2n=Sx2n=Bx2n+1,y2n+1=Tx2n+1=Ax2n+2(n=0,1,2,…),由式(1)有

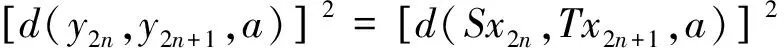
δd(Ax2n,Sx2n,a)d(Bx2n+1,Tx2n+1,a)+bd(Ax2n,Tx2n+1,a)d(Ax2n,Sx2n,a)+

cd(Bx2n+1,Sx2n,a)d(Bx2n+1,Tx2n+1,a)+λd(Ax2n,Tx2n+1,a)d(Bx2n+1,Sx2n,a)=

δd(y2n-1,y2n,a)d(y2n,y2n+1,a)+bd(y2n-1,y2n+1,a)d(y2n-1,y2n,a)=

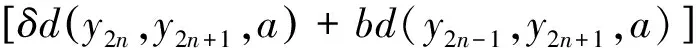
(2)

在式(2)中取a=y2n-1,得d(y2n,y2n+1,y2n-1)=0,从而由三角形面积不等式和式(2)得

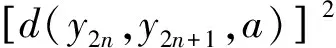
(3)

由于二次方程

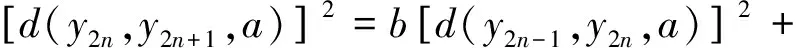
有解

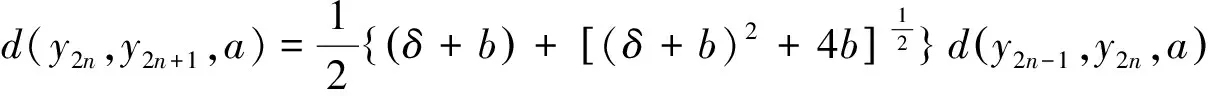
(4)

于是由式(3)与(4)得

d(y2n,y2n+1,a)≤βd(y2n-1,y2n,a),

(5)

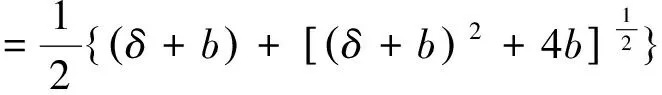
同理可证

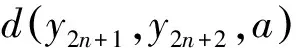
(6)

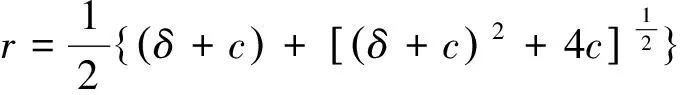
由式(5)与(6)有

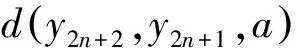
(7)

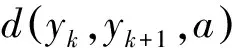
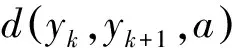
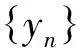
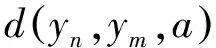
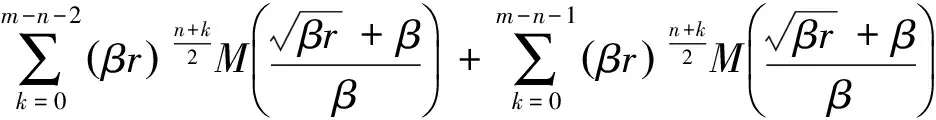
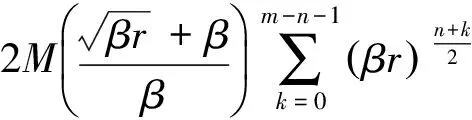
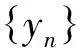
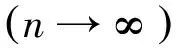
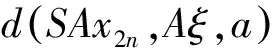
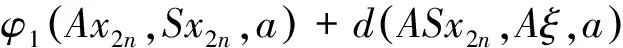
由式(1)有

[d(SAx2n,Tx2n+1,a)]2≤ δd(A2x2n,SAx2n,a)d(Bx2n+1,Tx2n+1,a)+bd(A2x2n,Tx2n+1,a)d(A2x2n,SAx2n,a)+

cd(Bx2n+1,SAx2n,a)d(Bx2n+1,Tx2n+1,a)+λd(A2x2n,Tx2n+1,a)d(Bx2n+1,SAx2n,a).

令n→∞,得

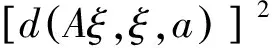
从而Aξ=ξ.

由式(1)有

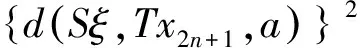
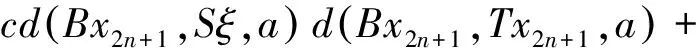
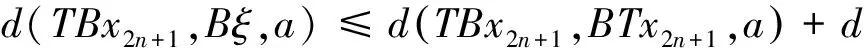
上式令n→∞,得TBx2n+1→Bξ.

由式(1)有

{d(Sx2n,TBx2n+1,a)}2≤ δd(Ax2n,Sx2n,a)d(B2x2n+1,TBx2n+1,a)+bd(Ax2n,TBx2n+1,a)d(Ax2n,Sx2n,a)+

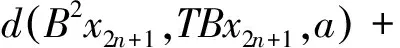
令n→∞,得

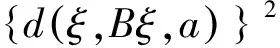
从而Bξ=ξ. 由式(1)有

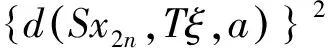
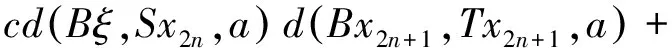
下证唯一性：假设u,v是S,T,A和B在X上两个不同的公共不动点,由式(1)有

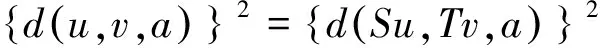
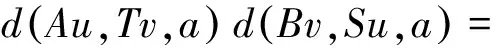
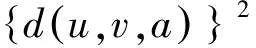
这是一个矛盾,故u=v.

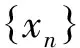
[1] FISHER B. Common fixed point mappings on complete and compact metric spaces[J]. Rev Roum Math,1980(2):217-222.

[2] 曾文智.关于映象对某些不动点定理[J].贵州大学学报(自然科学版),1988,5(1)：22-26.

[3] 张树义.Fisher型映象的不动点定理[J].长沙大学学报(自然科学版),2000,14(4)：22-24.

[4] 张树义.完备度量空间上四个映射的公共不动点[J].沈阳师范学院学报(自然科学版),1998(4)：20-23.

[5] 张军贺,谷峰.2-距离空间中两对非相容映象的一个新的公共不动点定理[J].西南师范大学学报(自然科学版),2012,37(4)：42-45.

[6] 郑晓迪,张树义.2-距离空间中两类Φ-压缩映象的公共不动点定理[J].杭州师范大学学报(自然科学版),2009,8(6)：429-431.

[7] 张树义.Altman型映象的公共不动点定理[J].烟台师范学院学报(自然科学版),2000,16(2)：95-97.

[8] 张树义,衣立红,邵颖.Altman型映象的公共不动点[J].杭州师范大学学报(自然科学版),2008,7(6)：401-404.

[9] ZHANG S Y, WANG L, SHIN S H, et al. Common fixed point theorems for a pair of orbitally contraction mapping[J]. Fixed Point Theory and Applictions,2003,5:191-195.

[10] 郑晓迪,万美玲,张树义,等.轨道压缩映射的几个新的不动点定理[J].北华大学学报(自然科学版),2014,15(4)：438-442.

[11] 张树义,宋晓光,栾丹.Φ-压缩映象的公共不动点定理[J].北华大学学报(自然科学版),2014,15(2)：167-173.

[12] 张树义,林媛.Φ-φ-型压缩映象不动点的存在性[J].北华大学学报(自然科学版),2016,17(1)：1-3.

[13] 张树义,赵美娜,刘冬红.弱相容映射几个新的公共不动点定理[J].江南大学学报(自然科学版),2015,14(6)：852-856.

[14] 张树义,赵美娜,李丹.关于平方型Altman映象的公共不动点定理[J].江南大学学报(自然科学版),2015,14(4)：472-477.

Common Fixed Point Theorem for Fisher Type Mapping in 2-metric Spaces

ZHAO Meina1, ZHANG Shuyi1, ZHENG Xiaodi2

(1. College of Mathematics and Physics, Bohai University, Jinzhou 121013, China; 2. Jinzhou Teacher’s Training College,Jinzhou 121001, China)

By using the concept of generalized guasi-commutativity, the existence and uniqueness of common fixed point for Fisher type contractive mapping involving four mappings are studied in complete 2-metric spaces, a new common fixed point theorem is proved, which improves and extends the corresponding results of some reference.

complete 2-metric space; Fisher type mapping; generalized guasi-commutativity; common fixed point

2016-07-02

国家自然科学基金项目(11371070).

张树义(1960—),男,教授,主要从事非线性泛函分析及应用研究.E-mail:jzzhangshuyi@126.com

10.3969/j.issn.1674-232X.2016.06.013

O177.91 MSC2010: 47H10; 54H25

A

1674-232X(2016)06-0632-04