基于类牛顿法配电网合环电流的分析计算

国网宿州供电公司 马廷稳 杨富民 陈云彩

基于类牛顿法配电网合环电流的分析计算

国网宿州供电公司 马廷稳 杨富民 陈云彩

合环是配电自动化重要功能之一。合环过程中，由于联络开关两侧存在电压差，可能会产生较大合环电流，这会对电力系统安全稳定运行产生极大影响。为提高辐射型馈线潮流计算的准确度，提出了类牛顿计算方法。其次考虑合环过程合环支路冲击电流对非合环支路的影响，进行了非合环支路冲击电流的推导。最后，通过算例仿真分析，验证了本文提出算法的高效性和准确性，对配电合环操作进行指导、为合环辅助决策系统的开发奠定理论基础。

合环操作；潮流计算；稳态电流；冲击电流

0　引言

配电网是电力企业连通用户的“最后一公里”。现阶段，我国配电网络一般“闭环设计，开环运行”，供电企业通过合环操作可实现不停电检修和故障下负荷转移[1-2]。然而，合环操作会产生合环环流，还会产生很大冲击电流，这可能会引起设备过载，短路电流越限，继电保护误动。因此，对合环操作进行研究，针对现有合环计算过程中存在的不足提出改进，具有现实意义。

配电网络潮流计算是合环操作的基础。文献[3]以分布系数为基础，实现对配电网络合环潮流的计算，该方需要人工计算，具有一定的准确度，仅适合于较为简单的环网潮流；文献[4]通过忽略负荷对配电网络的影响，建立冲击电流频域模型，以拉氏变换实现冲击电流瞬时值的求解，但变换过程计算量较大，工程应用难度较大，且其分析过程并为涉及非合环支路；以潮流计算为基础，通过戴维南等效，实现网络合环稳态电流和冲击电流的计算。[5]

针对现有合环潮流计算分析过程中的问题，本文基于前推回代，通过理论推导,得到更适合辐射馈线网络大规模应用的潮流计算方法,并基于迭代法实现上级网络的等值阻抗进行求解，对合环稳态电流、冲击电流及非合环支路电流进行推导，算例证明了本文提出方法的有效性。

1　基于潮流计算的配电网合环电流计算方法

1.1类牛顿法原理[6]

在直角坐标系中，节点注入功率可表示为：

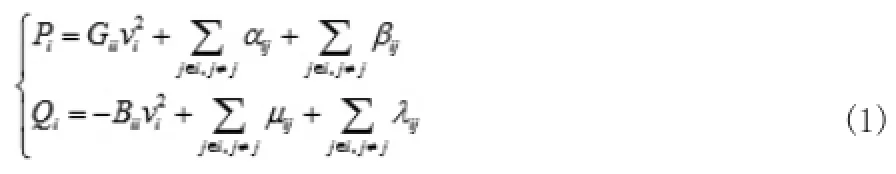
现定义：

由于功率损耗的存在，有：

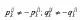
由上式，可假设：

从式(2)有：

对网络中的支路定义功率方向，在以上假设条件下，将方程(4)改写为矩阵形式为：

其中B为表征方向的节点,L为支路关联矩阵。在式(7)中，电压为常量，节点功率作为输入变量，则有：

式中ΔW为节点注入残差向量,ΔL为各支路待求功率改变向量。

在由辐射型馈线构成的配电网络中，直路数与节点数相同，由公式：

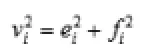
对方程两侧求导，用方程(4)的假设，则有：

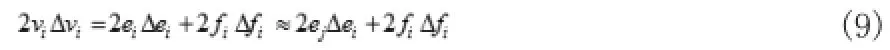
依据前推回代法思想，对式(2)两侧求导，结合方程(9)可得：

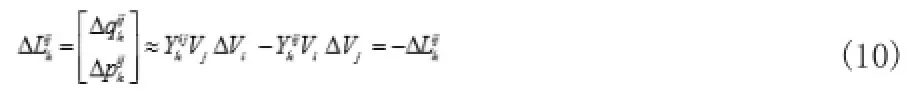
将上式改写为矩阵形式有：

综合式(8)，式(11)有：

式(13)为类牛顿法求解形式，式(13)为雅克比矩阵分解公式。

1.2合环稳态电流求取

以类牛顿法对配电馈线网路潮流进行求解，得到合环开关两侧电压分别为U1，U2，若母线I到母线II之间的阻抗为Z12上级网络的等值阻抗为Zeq，则由合环开关两侧引起的稳态环流为：

若馈线1初始电流为I1，馈线2的初始电流为I2，则合环后流经馈线1的合环环流为：

流经馈线2的电流为：

2　合环暂态电流分析

2.1合环冲击电流计算

由于电感元件的存在，合环环流包括周期分量和非周期分量，最大的合环全电流表达式为：

上式：Im为稳态合环电流幅值；Ta=L/R合环电流非周期分量时间常数；L为合环电路等值电抗；R为合环电路等值电阻；ω为系统额定频率。

一般在合环后的1/2T时，合环冲击电流出现瞬时最大值，令冲击系数，则冲击电流的最大瞬时值和最大有效值分别为：

2.2非合环支路冲击电流分析[7]

由非合环支路暂态过程，可知其瞬时电流表达式为：

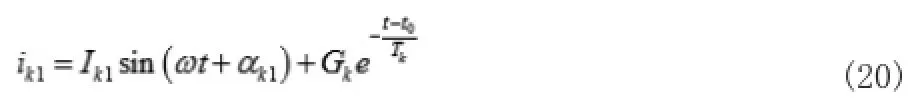
上式：Ik1为非合环支路初始稳态电流幅值； αk1为其初始相角；Tk为非周期分量时间常数；Gk为非周期分量初始值；t0为合环时间。

k支路合环前的电流为：

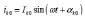
上式：Ik0和αk0分别为非合环支路初始幅值和相角。由电流的不可突变性，非合环支路冲击电流初值直流分量为：

式(21)可写为：

在非合环支路中，合环前相角初值αk0和合环后相角初值αk1可能偏差较大，因此冲击电流最大值可能不出现在合环后的1/2T时刻，假定冲击电流瞬时最大值在t1时刻出现，则有：

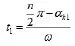
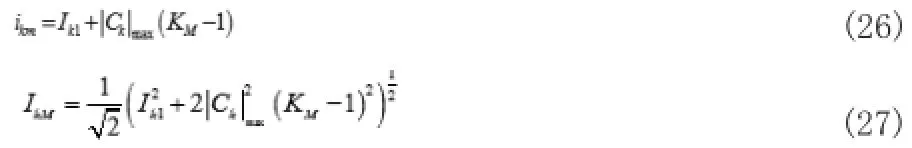
3　算例分析

采用我国SZ地区配电网络作为分析算例，共选取23个联络开关，数据采用PMS导出,所有参数均归算到10kV侧，合环结构示意图如1所示：

图1　SZ地区典型合环网络

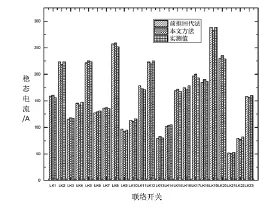
图2 稳态电流结果比较

图1中给出了SZ城区三种典型的合环方式：(1)同一变电站同一区域内馈线合环：联络开关LK01。(2)同一变电站不同区域馈线合环：联络开关LK02，联络开关所连接馈线来自同一变电站的不同区域，但其上级电源来自相同区域。(3)不同变电站馈线之间合环：联络开关LK03，两侧馈线分别来自不同变电站。

分别以本文所提出的潮流算法和前推回代法为对配电网络进行潮流计算，并依据式(15)、(16)、(17)计算得到各支路合环稳态电流如图2所示：

以潮流计算为基础，根据式 (24)计算得到各支路合环冲击电流最大有效值如图3所示：

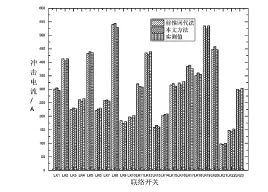
图3　冲击电流结果比较

由图2，图3：本文所提方法与前推回代法计算精度相同或近似，但本文方法避免了前推回代初始在计算开始需进行拓扑分析。另外本文推导的方法与传统牛顿法在求解过程、编程思想上相同，更加适合大规模配电网络的工程应用。

依据式(27)计算合环网络中非合环支路冲击电流值，如图4所示：

图4　非合环支路最大冲击电流比较

由图4，在合环的过程中，非合环支路6的冲击电流超过其馈线最大载流400A，这可能会对电力系统的安全稳定运行造成重大影响。故在合环过程中有必要对非合环支路的冲击电流进行综合考虑。

4　结语

由于合环电流的存在，配电网络合环操作会影响电力系统安全稳定运行。本文以类牛顿潮流计算为基础，进行了合环稳定电流、冲击电流、非合环电路冲击电流计算公式进行推导；针对上级电网等效电阻难以直接统计，以迭代法进行求取，并应用于实际仿真计算。算例结果表明，本文所推导计算公式可对相关合环电流进行准确的计算，为合环操作辅助决策系统的开发提供了理论支撑。

[1]杨志栋,刘一,张建华等.北京10kV配网合环试验与分析[J].中国电力,2006(3):66-69.

[2]李庆彪,贾秉健,李志博.配电网合环潮流的分析与控制措施[J].中国电业:技术版,2013(06):88-92.

[3]李江华.浅析10 kV 配网合环产生环流的原因及预防措施[J].电网技术,2006,30(增刊):199-201.

[4]葛少云,李晓明.基于戴维南等值的配电网合环冲击电流计算[J].电力系统及其自动化学报, 2007(6):124-127.

[5]汲亚飞,赵江河.辐射型配电网合环稳态电流计算方法研究[J].电力系统保护与控制,2009(12).

[6]甘国晓,王主丁,李瑞等.配电网合环冲击电流计算方法及其简化计算公式[J].电力系统自动化,2014(20):115-120.

[7]汪芳宗,向小民,等.放射形配网潮流计算的一种新的牛顿法[J].计算机技术与自动化, 2007(2):46-50.