基于向量式有限元法的风力发电机组一体化仿真分析

陈俊岭，阳荣昌，马人乐

(1.同济大学 建筑工程系，上海 200092; 2. 同济大学 建筑设计研究院(集团)有限公司，上海 200092)



基于向量式有限元法的风力发电机组一体化仿真分析

陈俊岭1†，阳荣昌2，马人乐1

(1.同济大学 建筑工程系，上海 200092; 2. 同济大学 建筑设计研究院(集团)有限公司，上海 200092)

大型风电机组为强非线性刚柔耦合的周期时变多体系统，传统有限元方法不能解决叶片转动过程中由于刚体位移而导致的刚度矩阵奇异问题，向量式有限元法可有效考虑叶片的几何非线性和大变形运动、塔架的弹性变形、气动载荷等因素.基于MATLAB平台编制空间梁系结构求解程序，选取悬臂梁受端部集中动荷载和欧拉梁绕定轴转动两个典型算例验证程序的正确性.建立包含机舱、轮毂、叶片和塔架在内的风电机组一体化仿真分析模型，根据机组静止状态下自由振动响应，用模态参数识别方法提取了机组的自振频率，计算结果与传统有限元法吻合.采用谐波叠加法和本征正交分解法相结合的方式，运用B样条曲面插值策略，模拟生成风电机组在正常运行状态下的风速时程.采用向量式有限元法对正常运行状态下的风电机组进行风振响应分析，较好地反映了重力对叶片内力周期性变化的影响以及叶片与塔架的共同作用.

风电机组；向量式有限元；仿真分析；运行状态；非线性分析

风电机组运行时，作用在叶片上的空气动力等外荷载使叶片和塔架产生振动，对风电机组关键部件造成疲劳损伤.因此建立包含塔架、叶片和机舱在内的风力发电机组一体化分析模型，对研究风力发电机组在不同运行状态下的动力响应具有重要意义.Lobitz[1]提出了风力发电塔“质量-阻尼-弹簧”模型，通过连接矩阵实现塔体和叶片的耦合.王介龙等[2]综合考虑叶片挥舞、摆振、扭转和轴向位移4种变形运动与机舱刚体运动、塔架弹性变形的强非线性耦合作用，采用子空间迭代法计算在二维拟定常风荷载作用下系统的动力响应.柯世堂等[3]基于风力机塔架-叶片耦合模型，采用改进的叶素动量理论模拟了考虑平稳风修正、叶片旋转效应和空间相干性的风力机气动载荷，并分析了气动响应.Prowell等[4]将顶部叶片和机舱视为集中质量点建立简化分析模型，通过与原型试验结果进行对比，发现简化分析模型对于整体结构的一阶动力特性精度几乎没有影响.刘雄等[5]基于模态分析方法建立了风力机叶片和塔架的耦合动力学模型.李永建等[6]采用柔性多体动力学方法建立了风力机叶片-机舱-塔架耦合动力学方程.

风电机组为强非线性刚柔耦合的周期时变多体系统，采用传统有限元方法不能解决叶片转动过程中由于刚体位移而导致的刚度矩阵奇异问题，只能将叶片、轮毂和机舱简化[7]；采用假设模态法不能考虑非线性问题，采用多体动力学方法进行建模无法体现结构的细部特征.而向量式有限元是基于向量力学与数值计算提出的一种新型数值计算方法[8-9]，可以有效处理连续体几何变形、非线性与不连续的材料本构关系、多个连续体与刚体的运动及其相互耦合行为等各种复杂情形.本文采用向量式有限元法，基于MATLAB平台编制空间梁系结构的求解程序，建了立包含机舱、轮毂、叶片和塔架在内的风电机组一体化仿真分析模型.

1 空间梁系结构向量式有限元法

向量式有限元是用一组空间点近似描述结构几何，以牛顿第二定律描述质点的运动，模型离散为空间点以及各点之间的物理关系，在一系列持续增加的时间点内描述结构变化[10].向量式有限元的分析对象为质点，因此，首先要将结构离散成一系列的空间质点，质点之间通过结构单元连接(图1).对于两结点空间梁单元，可将两端结点取为质点，并将杆件的质量mi凝聚在质点处.质点上的荷载包括作用在其上的外力、单元对质点的内力以及阻尼力，三者一起影响质点的运动轨迹.质点数量越多，计算结果也越精确，但计算量会相应增加.

图1 向量式有限元示意Fig.1 Scheme of vector form intrinsic finite element

在向量式有限元中，称时间段ta≤t≤tb内满足标准化控制方程的计算单元为途径单元[11].途径单元是更新单元内力的基础，当结构具有复杂行为过程时，可以通过引入足够多的途径单元使得时间段足够小，则在这个时段内可认为构件的几何变形很小，可以用大变位和小变形理论来处理.若以ta时刻单元的状态为参考，只要求得内力增量，则tb时刻单元的内力便可获得，求解内力增量的关键是计算单元在该时间段内的纯变形.为求得单元在时间段内的纯变形，可令单元作虚拟的刚体平动和刚体转动(即逆向运动)[11].取ta时刻梁的构形为参考构形，单元从ta时刻起始位置IaJa运动到tb时刻的位置IbJb，其逆向运动即为：首先将IbJb平移使得质点Ib和质点Ia重合，接着再以Ia为中心转动至与IaJa在同一直线到达虚拟位置I’J’，则IaJa和I’J’之间的形态差异即为纯变形(图2).将初始的位移与角度定义为向量，逆向平移与旋转均可以通过向量运算来完成，求得单元在虚拟位置上的单元内力之后，再进行与逆向运动相反的正向运动恢复至当前时刻的位置，而在正向运动的过程中，平移不改变内力大小和方向，旋转只改变内力的方向不改变大小，这样就求得当前时刻单元的内力.

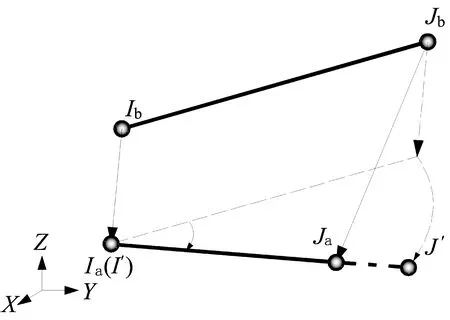
图2 空间梁单元逆向运动Fig.2 Reverse movement of space beam-element

2 计算程序验证

基于向量式有限元理论，采用MATLAB编制了风电机组整体动力学分析程序，主要受力部件用空间梁单元模拟.选取悬臂梁受端部集中力作用(动载)和欧拉梁绕定轴转动2个典型算例验证程序的正确性.

2.1 悬臂梁受端部集中力作用(动载)

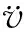
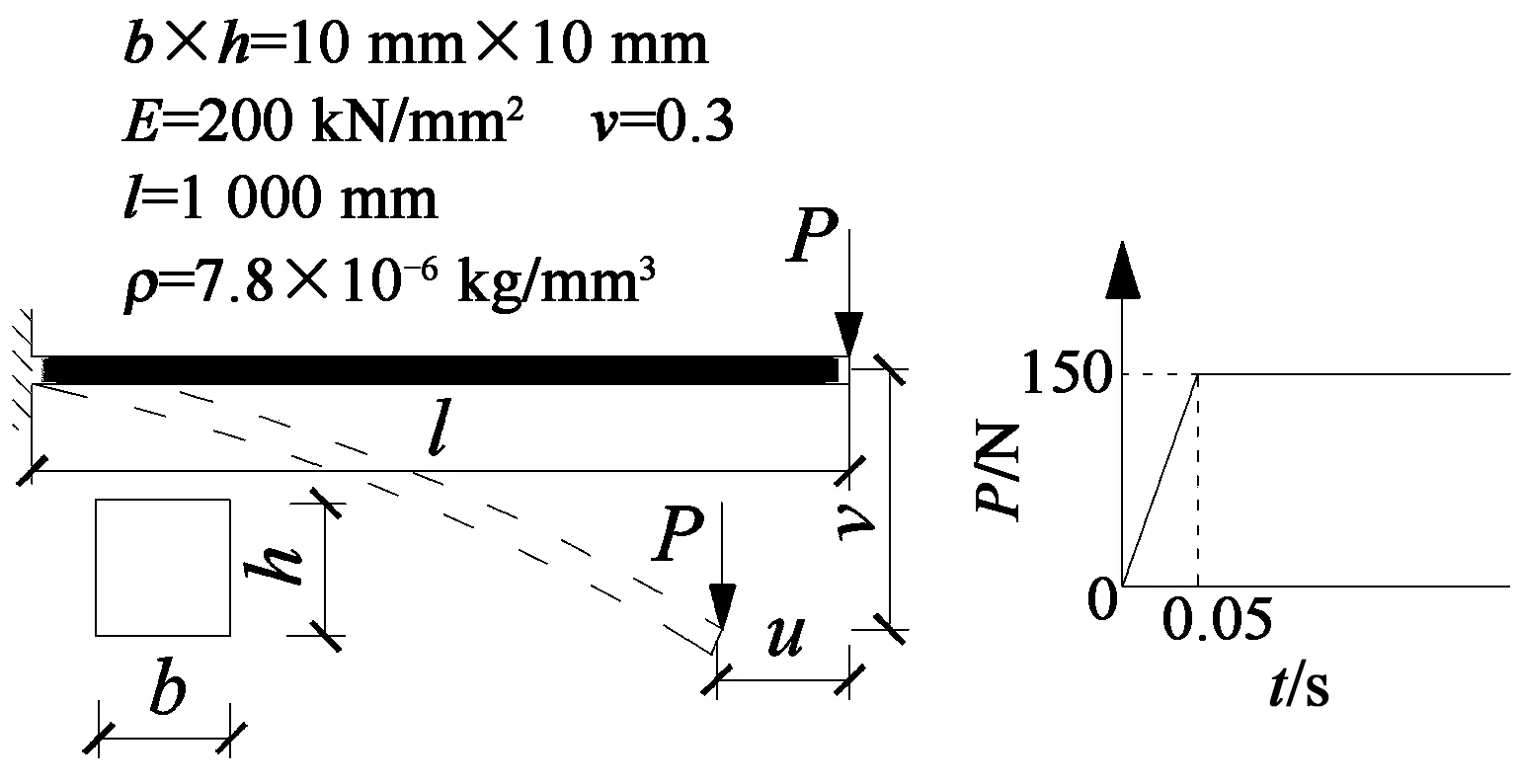
(a) 相关计算参数

时间/s (b) 端点加速度响应图3 悬臂梁端部突然加载Fig.3 Impulsive loading at the cantilever beam end

2.2 欧拉梁绕定轴转动

图4(a)为无限刚欧拉梁绕定轴转动示意图，若长度为l，单位长度质量为ρ，横截面面积为A，根据理论力学可求得梁端无量纲位移u/l的解析解(见式(1)).传统有限元法无法求解刚体转动问题，而向量式有限元则可有效处理该类问题.模拟时共划分5个单元，阻尼系数取0，时间步长取1×10-4s，梁端无量纲位移u/l的时程曲线见图4(b).从图中可看出，向量有限元计算结果和解析解吻合.

(a) 相关计算参数

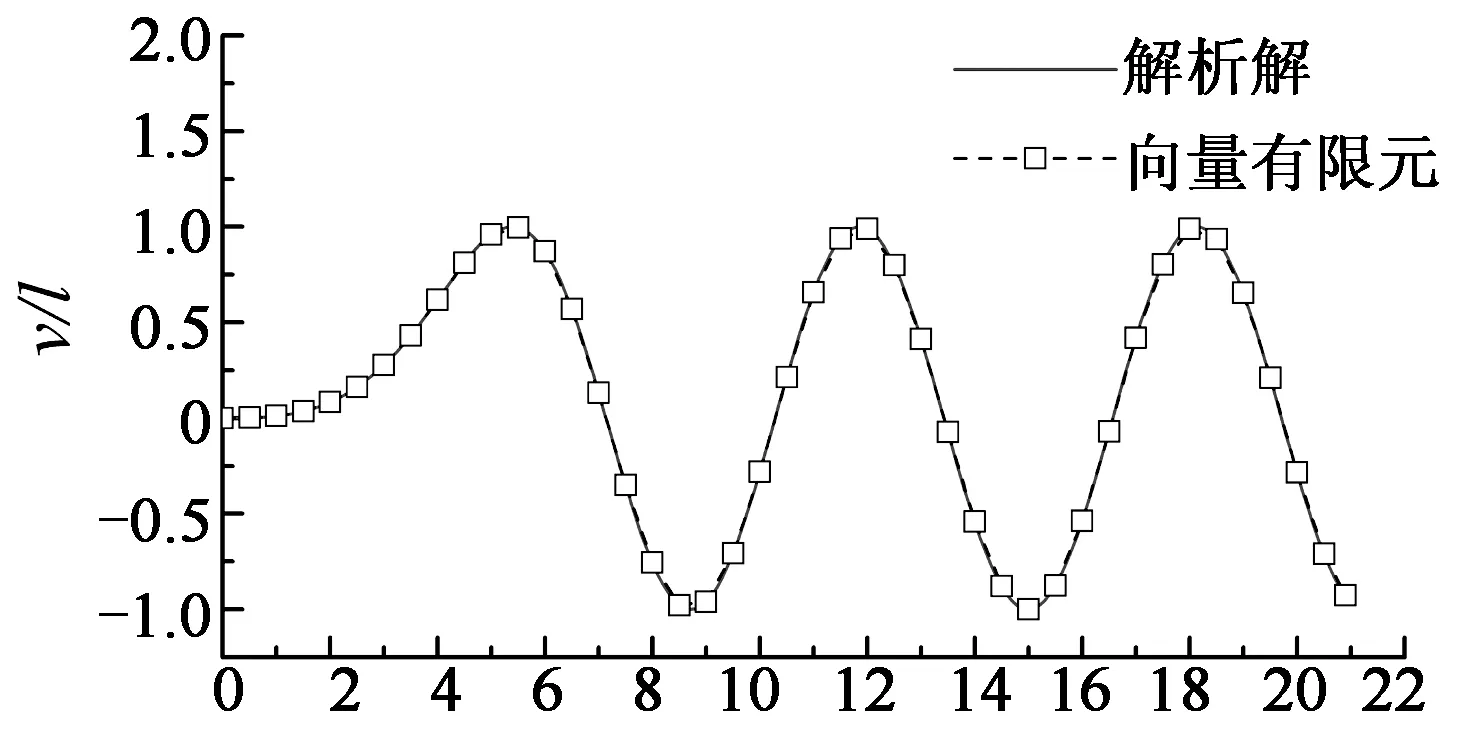
时间/s (b) 端点位移响应图4 欧拉梁绕定轴转动情况Fig.4 Rotation of Euler beam around a fixed axis

(1)

3 风电机组整体动力学模型

3.1 模型建立

风电机组由叶片、塔架、机舱等部件组成，机舱内部构造虽然非常复杂但并不是本文关注的重点，因此本文在整体建模时将机舱简化为一根刚性梁(图5).轮毂和机舱在各自质心位置凝聚成质点，机舱质点和轮毂质点分别与塔架顶部质点、各叶根质点与轮毂质点、各叶根质点之间通过刚性梁连接.当风电机组处于运行状态时，释放塔架顶部质点绕X轴的转动自由度使得叶片能够旋转；若机组处于停机状态，只需取消自由度释放即可；若需要模拟机组的偏航过程，只需释放塔架顶部节点绕塔架轴线的转动自由度.文中以某1.5 MW机组为例，主要参数如下：轮毂高度65 m，风轮直径75 m；塔架底部直径4.2 m，顶部直径2.74 m；底部壁厚25 mm，顶部壁厚20 mm，其余部分基本从25 mm线性减小至12 mm；机舱总质量66 t，轮毂质量16 t；塔架材料为Q345钢材.组装后的风电机组整体模型如图6所示.

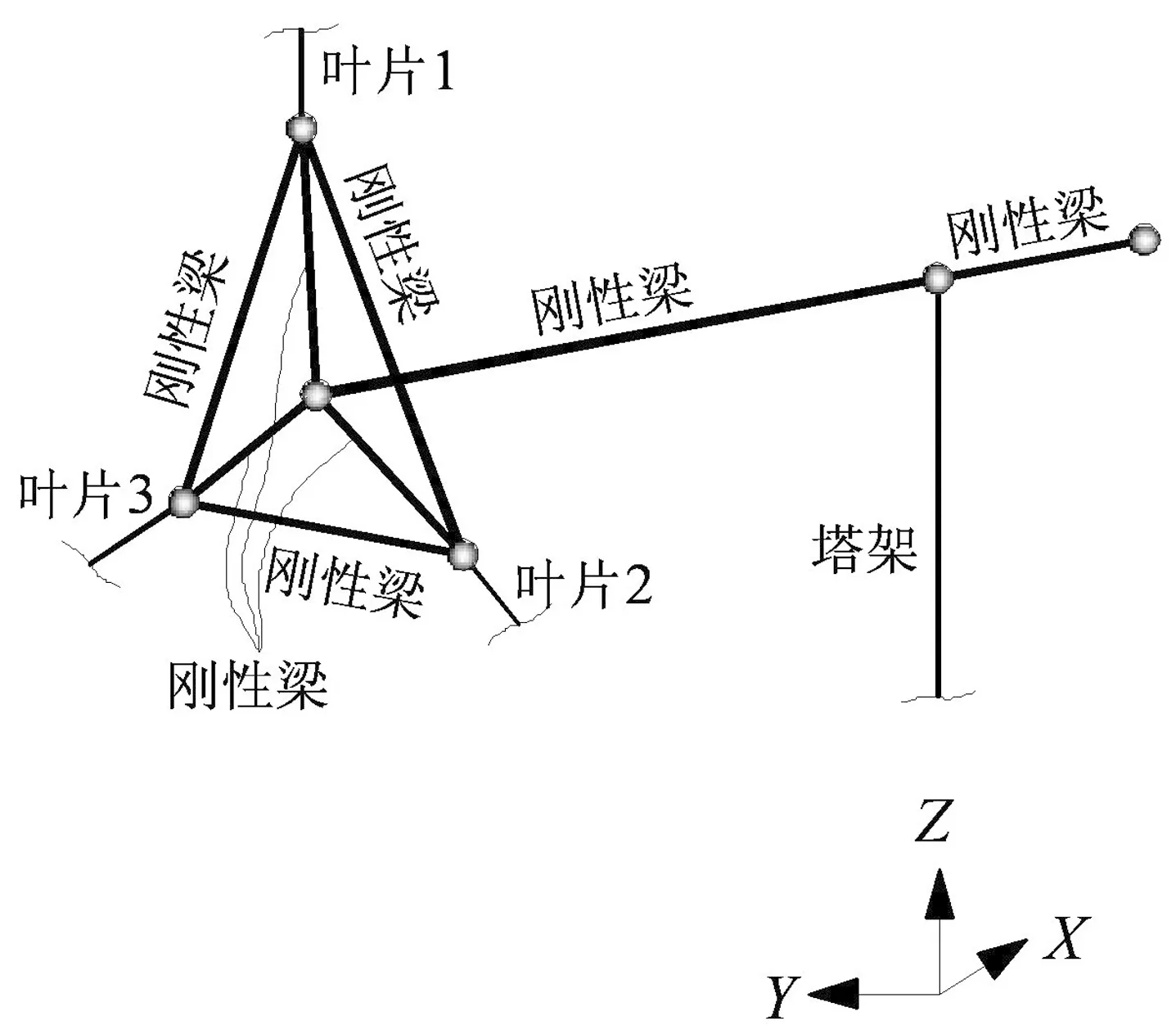
图5 风机各部件间的连接Fig.5 Connections among components of wind turbine

图6 风电机组整体模型Fig.6 Integated model of wind turbine

3.2 关键参数取值

3.2.1 时间步长

运用中心差分法在求解结构非线性动力响应时的稳定性受时间步长影响，时间步长Δt必须小于临界值Δtcr(见式(2)).

(2)

式中：Tn为系统的最小自振周期，可用最小尺寸单元的最小自振周期代替[12].因此，在将模型空间离散时需要选择合适的单元尺寸，则Δtcr根据单元的最小尺寸L按式(3)近似求得.

(3)

式中：E和ρ分别为材料的弹性模量和密度.当不考虑刚性梁、机舱和轮毂集中质量影响时，根据式(4)估算的Δtcr的量级为10-4s，最终选取时间步长Δt为4×10-5s.

3.2.2 阻尼系数

传统有限元分析中采用瑞利阻尼假定 (见式(4))，但向量式有限元中无刚度矩阵的概念，因此需要将振型阻尼比等效成阻尼系数.

C=αM+βK

(4)

其中，C为阻尼矩阵；M和K分别为质量矩阵和刚度矩阵；α和β分别为质量阻尼系数和刚度阻尼系数.瑞利阻尼模型下第n阶阻尼比ξn，可表述为式(5)[13].

(5)

当给出任意两阶振型的阻尼比时，α和β可根据式(5)得到的两个联立方程求得.根据文献[14]的取值，叶片和塔架所有模态的阻尼比取1%.在计算叶片阻尼系数时ωm,ωn分别取叶片前两阶弯曲振动模态对应圆频率，在计算塔架阻尼系数时ωm,ωn分别取塔架前两阶顺风向模态对应圆频率.由于在向量式有限元中不存在刚度矩阵，且β主要对高频起作用，所以可通过适当提高α的方式考虑β的影响，具体取值可通过自由衰减数值试验确定.

3.3 停机状态下模态分析

采用传统有限元法建立塔架的整体模型进行模态分析，前10阶模态列于表1.

表1 传统有限元和向量式有限元计算所得自振频率

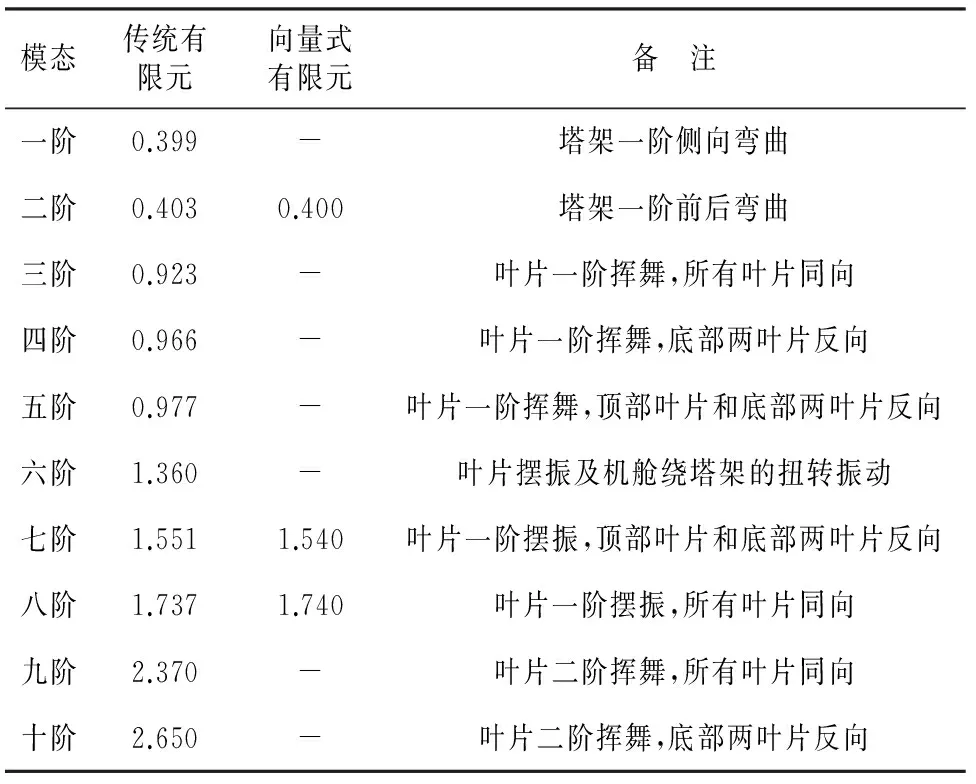
Tab.1 Natural frequencies by traditional finite element and vector form intrinsic finite element Hz

将有限元法的结点转换成质点，保持单元结点的连接关系、材料及截面属性不变，将模型转换成向量式有限元模型，基于结构的响应通过峰值法识别结构自振频率[15].通过在0.1 s内对轮毂处突然施加200 kN水平荷载，使机组在停机状态自由振动，阻尼系数取0，提取典型质点的加速度时程用于模态识别.由于突加荷载使得机组产生前后方向的振动，只能识别前后振动对应的那部分模态的频率，识别结果同样列于表1.从表中可以看出，基于向量式有限元响应所识别的频率和有限单元法计算结果也十分接近，若以有限单元结果为基准，最大误差为1.6%，由此验证了向量式有限元模型的正确性.

4 风振响应分析

风电机组在不同的运行状态下因风轮的转动所受风荷载并不相同，正常运行状态下叶片的旋转使得叶片上平均风随时间变化，如果荷载不经处理而直接施加会造成突然加载的现象，使得机组的动力响应失真.为避免产生突然加载的现象，在荷载时程前续一段持时20 s的从0缓慢增加至实际值的时程.由于风荷载模拟的时间间隔和中心差分时间步长不一致，中间时刻的风速通过线性插值计算.风振响应分析时外部荷载条件为：轮毂高度处平均风速为额定风速11 m/s，叶片转速为额定转速17.4 r/min，考虑重力荷载.

4.1 风速时程模拟

采用谐波叠加法和本征正交分解法相结合的方式，运用B样条曲面插值策略，模拟生成风电机组在正常运行状态下的风速时程，主要步骤如下[16]：首先，确定风轮平面内和塔架上的采样点分布形式及风速模拟的截止频率、地貌等相关参数；然后，由谐波叠加法模拟采样点处的脉动风速时程，并用本征正交分解法将风轮平面内采样点的脉动风速时程进行分解；接着，不断更新叶片位置，用B样条曲面插值法求得叶片上插值点的本征模态值并根据本征正交分解法重构当前时刻的脉动风速，直到模拟时间结束；最后，将各个时刻的脉动风速汇总并和平均风叠加形成总的风速时程.风速模拟参数见表2，生成的轮毂质点和叶尖质点1处的风速时程见图7.叶片上风荷载按照叶素动量理论方法计算，单管塔和机舱风荷载体型系数分别取0.6与1.2.

表2 风速模拟参数Tab.2 Parameters for wind simulation

4.2 风振响应

将外荷载施加于相应质点，采用向量式有限元法对机组正常运行状态下的风振响应进行分析，提取叶片转速达到目标值以后200 s的响应，塔架顶部加速度响应和塔架底部风轮平面外弯矩响应如图8所示.从图中可以看出，在正常运行阶段，塔架顶部位移最大值为280 mm，约为塔架高度的1/232.根据VDI3834[17]规定：风电机组正常运行的机舱加速度均方根限值为0.3 m/s2，计算值为0.28 m/s2，主机厂要求正常运行阶段的加速度最大值不超过0.1g，计算所得最大幅值为0.89 m/s2.

时间/s (a) 轮毂质点风速时程

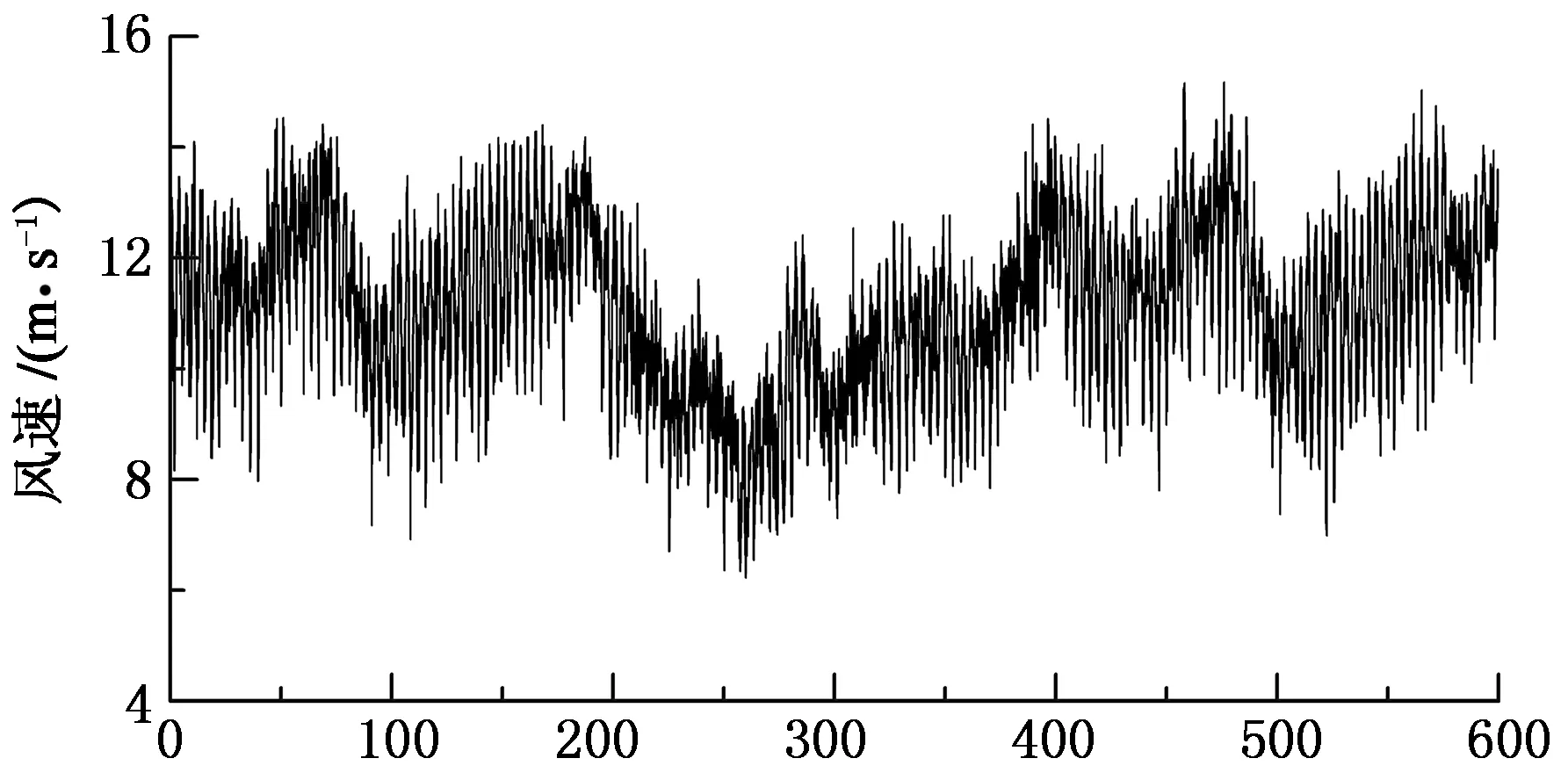
时间/s (b) 叶尖1质点风速时程图7 典型质点风速时程Fig.7 Time history at typical particles

时间/s (a)塔顶加速度时程

时间/s (b) 塔底弯矩图8 塔顶加速度和塔底弯矩Fig.8 Top acceleration and base moment of the tower

以叶片1为例给出叶片根部的轴力、风轮平面外弯矩和剪力响应如图9所示.从图中可以看出，叶根的轴力和平面内剪力主要呈正弦式波动，这主要是由于叶片受重力荷载作用并周期性转动所致.虽然面内剪力比面外幅值小，但是对叶片的疲劳寿命也有重要的影响，因此在进行风电机组风振响应分析时必须考虑重力的影响.

时间/s (a) 叶根轴力

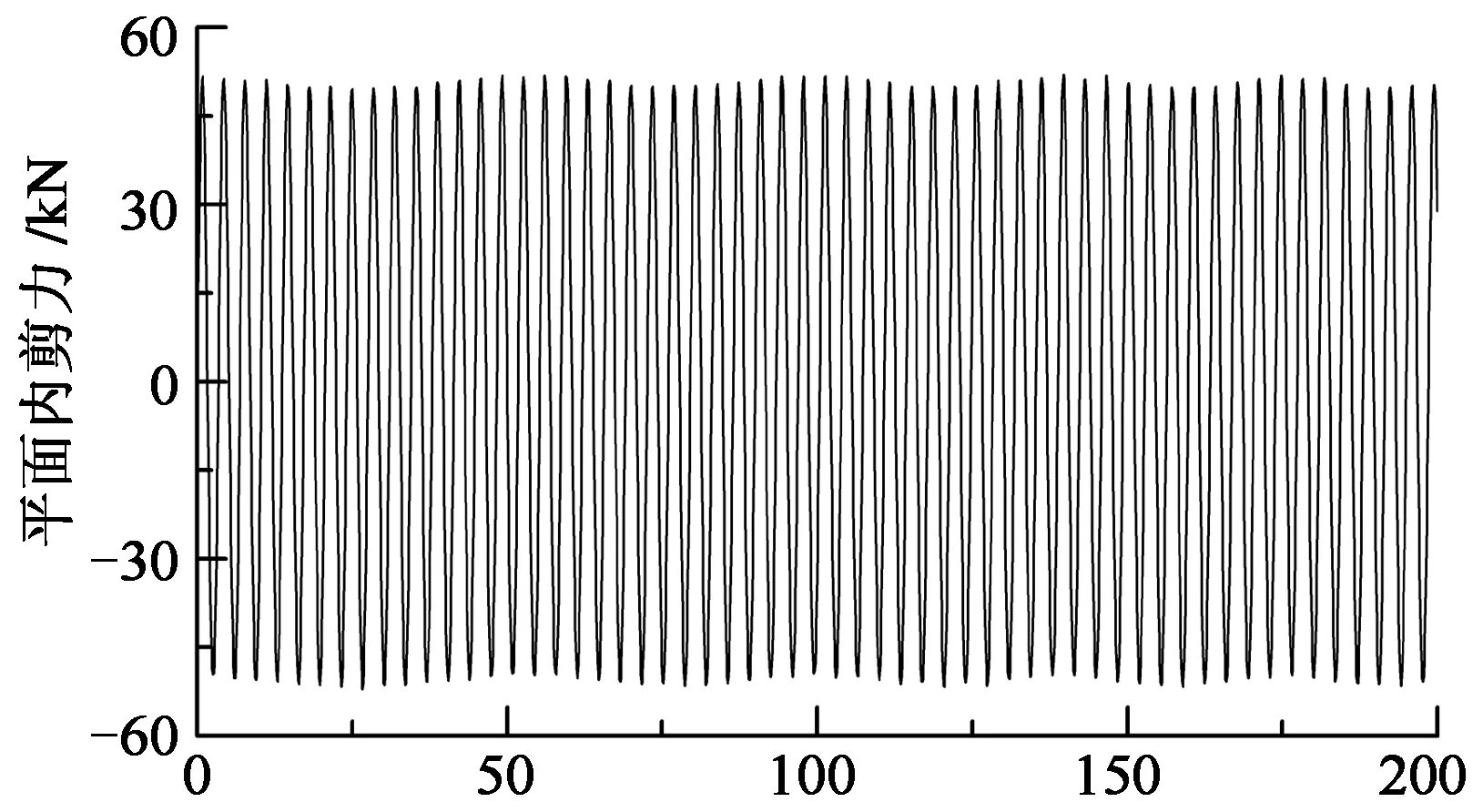
时间/s (b) 叶根风轮平面内剪力

时间/s (c) 叶根风轮平面外剪力

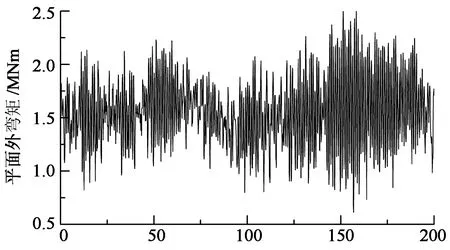
时间/s (d) 叶根风轮平面外弯矩图9 叶根内力Fig.9 Internal force at the root of blade

将典型响应变换至频域以考察其响应谱特征(见图10).图10(a)为塔顶x向加速度响应谱，从图中可以看出，塔顶加速度以共振响应为主且受到多个振型影响，主要以整体一阶和叶片挥舞一阶为主，高频振型影响相对较小.图10(b)为塔底弯矩响应谱，从图中可以看出，塔底弯矩的共振响应主要以整体一阶振型为主，叶片与塔架的相互作用也有一定影响.图10(c)为叶尖x向位移响应，背景响应同样占很大部分，而共振响应主要叶片挥舞一阶为主，在1P和2P处有峰值.图10(d)为叶根平面外弯矩响应谱，从图中可以看出，叶根平面外弯矩的能量分布和叶尖x向位移响应谱相似，共振响应受到多个振型影响，1P和2P处也有较明显的峰值，但主要以叶片挥舞一阶为主.

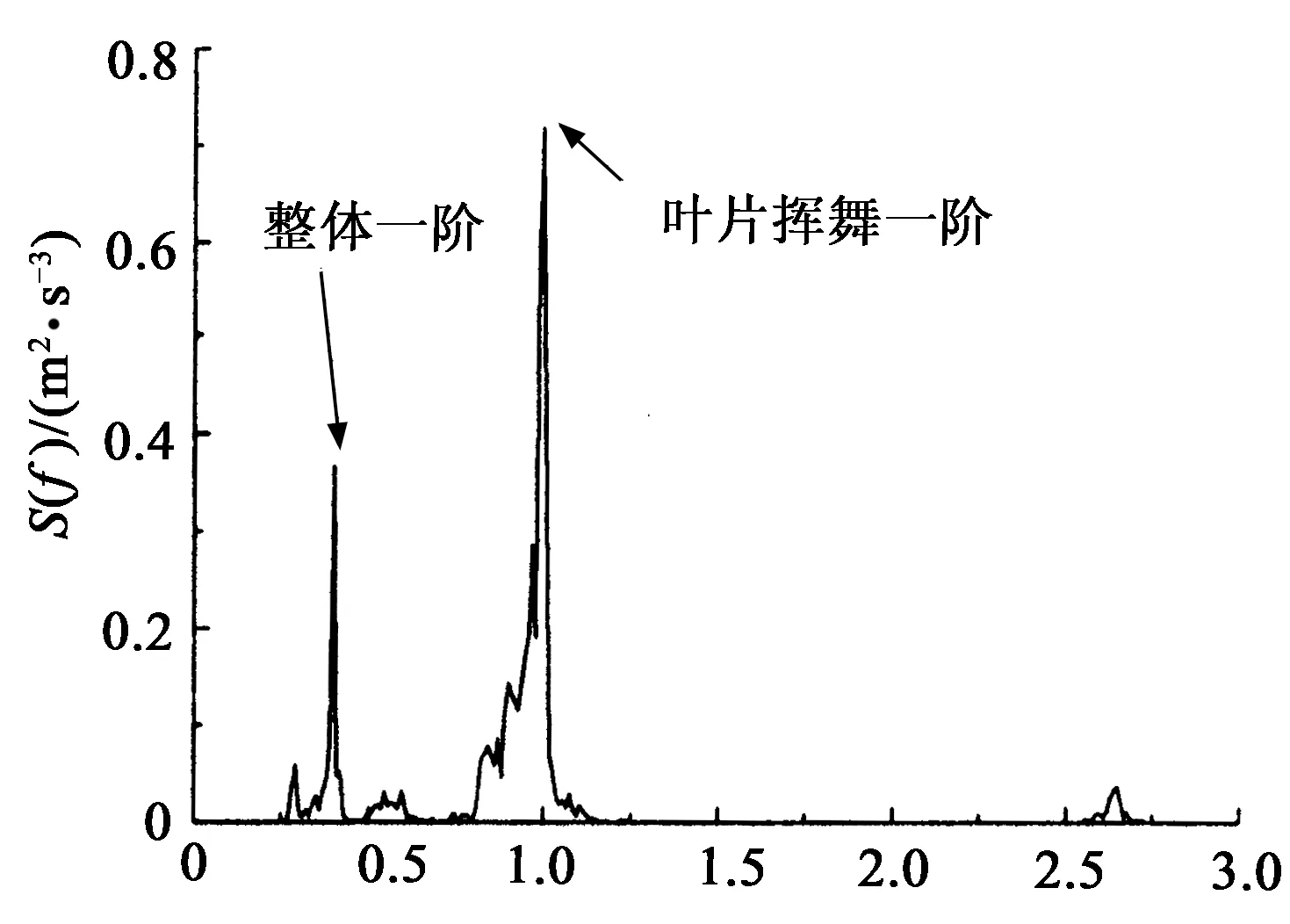
频率/Hz (a) 塔顶x向加速度响应谱

频率/Hz (b) 塔底弯矩响应谱

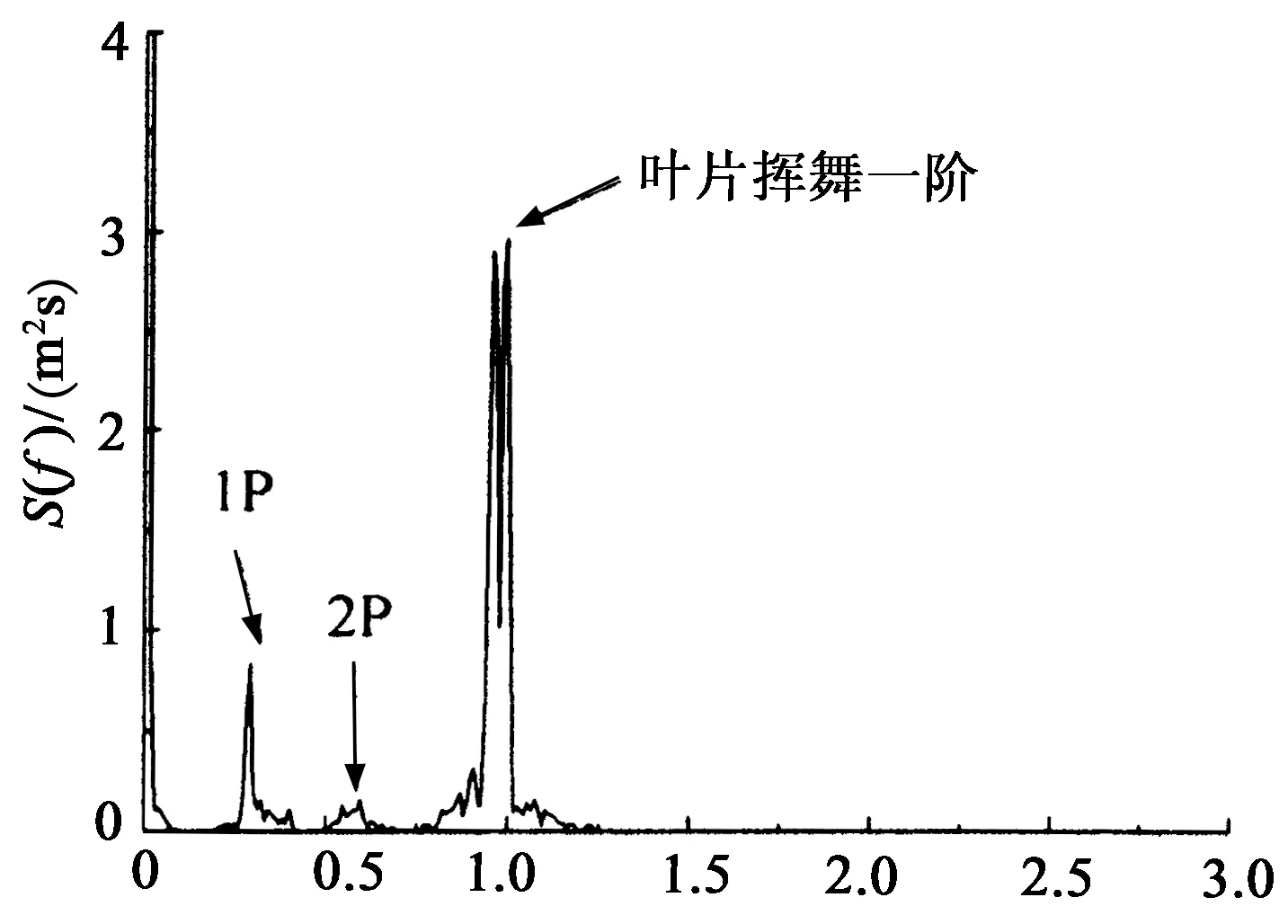
频率/Hz (c) 叶尖x向位移响应谱

频率/Hz (d) 叶根平面外弯矩响应谱图10 典型响应谱Fig.10 Spectra of typical dynamic responses

5 结 论

本文采用向量式有限元法建立了风力发电机组一体化仿真分析模型，分析了风电机组在静止状态下的自振特性和正常运行状态下的风振响应.主要结论如下：

1)基于向量式有限元方法通过自由振动响应识别的机组频率和基于传统有限元法计算所得结果吻合较好，验证了向量式有限元模型的准确性.

2)采用向量式有限元方法建模，可以较好反映重力对叶片内力周期性变化的影响，这种周期性变化对叶片的疲劳寿命不利，但对于塔架的影响相对较小.

3)正常运行状态下塔顶位移和塔底弯矩的共振响应主要以整体一阶振型为主，但叶片与塔架的相互作用也有一定影响；塔顶加速度响应则以共振响应为主且受到多个振型影响，其中整体一阶和叶片挥舞一阶贡献较大.叶尖平面外位移和弯矩响应中背景响应都占很大部分，而共振响应主要以叶片挥舞一阶为主；面内位移则主要受定轴转动影响，在叶片转动频率处存在尖峰.

[1] LOBITZ D W. A nastran-based computer program for structural dynamic analysis of horizontal axis wind turbines[C]//Proceedings of the Horizontal Axis Wind Turbine Technology Workshop. Cleveland:Department of Energy and NASA-Lewis, 1984.

[2] 王介龙, 陈彦, 薛克宗. 风力发电机耦合转子/机舱/塔架的气弹响应[J] .清华大学学报:自然科学版, 2002, 2(2):211-215.

WANG Jie-long, CHEN Yan, XUE Ke-zong.Aeroelastic response analysis of coupled rotor/nacelle/tower for a horizontal axis wind turbine[J]. Journal of Tsinghua University :Science and Technology, 2002,2(2): 211-215. (in Chinese)

[3] 柯世堂,曹九发,王珑,等. 风力机塔架-叶片耦合模型风致响应时域分析[J].湖南大学学报:自然科学版, 2014, 41(4):87-93.

KE Shi-tang, CAO Jiu-fa, WANG Long,etal. Time-domain analysis of the wind-induced responses of the coupled model of wind turbine tower-blade coupled system[J]. Journal of Hunan University:Natural Sciences, 2014, 41(4):87-93.(In Chinese)

[4] PROWELL I, VELETZOSM, ELGAMALA,etal. Experimental and numerical seismic response of a 65 kW wind turbine[J]. Journal of Earthquake Engineering, 2009, 13:1172-1190.

[5] 刘雄, 张宪民, 陈严,等. 水平轴风力机结构动力响应分析[J]. 太阳能学报, 2009, 30(6):804-809.

LIU Xiong, ZHANG Xian-min, CHEN Yan,etal. Structure dynamic response analysis of horizontal axis wind turbines[J]. ACTA Energiae Solaris Sinica, 2009, 30(6):804-809.(In Chinese)

[6] 李永建, 殷玉枫,丁健刚,等. 随机风载荷下大型风力机叶片/机舱/塔架耦合动力学分析[J]. 可再生能源, 2014, 32(7):992-997.

LI Yong-jian,YIN Yu-feng,DING Jian-gang,etal. Coupling dynamics analysis on blades/nacelle/tower of large-scalewind turbine with stochastic wind load[J]. Renewable Energy Resources, 2014, 32(7):992-997.(In Chinese)

[7] 陈俊岭，阳荣昌，马人乐. 大型风电机组组合式塔架结构优化设计. 湖南大学学报:自然科学版, 2015, 42(5):29-35.

CHEN Jun-ling, YANG Rong-chang, MA Ren-le. Design optimization of wind turbine tower with composite structure using particle swarm approach[J]. Journal of Hunan University:Natural Science, 2015, 42(5):29-35. (In Chinese)

[8] TING E C, SHI H C, WANG Y K. Fundamentals of a vector form intrinsic finite element: Part 1.Basic procedure and a plane frame element [J].Journal of Mechanics, 2004, 20(2):113-122.

[9] TING E C, SHI H C, WANG Y K. Fundamentals of a vector form intrinsic finite element: Part 2.Plane solid element [J].Journal of Mechanics,2004,20(2):123-132.

[10]朱明亮，董石麟. 基于向量式有限元的弦支穹顶失效分析[J]. 浙江大学学报:工学版，2012，46(9):1611-1618, 1632.

ZHU Ming-liang, DONG Shi-lin. Failure analysis of suspen-dome by vector form intrinsic finite element method[J]. Journal of Zhejiang University:Engineering Science, 2012，46(9):1611-1618, 1632.(In Chinese)

[11]喻莹,罗尧治.基于有限质点法的结构屈曲行为分析[J].工程力学,2009,26(10):23-29.

YU Ying, LUO Yao-zhi. Buckling analysis of structures by the finite particle method[J]. Engineering Mechanics,2009,26(10):23-29.(In Chinese)

[12]王勖成.有限单元法[M].北京:清华大学出版社,2003:617-662.

WANG Xu-cheng. Finite element method[M]. Beijing: Tsinghua University Press,2003:617-662. (In Chinese)

[13]CLOUGH R W,PENZIEN J. Dynamics of structures[M]. Berkeley, Calif:Computers and Structures Inc, 2004: 234-245.

[14]WOUDEV C, NARASIMHAN S. A study on vibration isolation for wind turbine structures[J]. Engineering Structures, 2014, 60: 223-234.

[15]马人乐, 马跃强, 刘慧群, 等. 风电机组塔筒模态的环境脉动实测与数值模拟研究[J]. 振动与冲击, 2011, 30(5):152-155.

MA Ren-le,MA Yue-qiang,LIU Hui-qun，etal. Ambient vibration test and numerical simulation for modes of wind turbine towers[J]. Journal of Vibration and Shock, 2011, 30(5):152-155.

[16]马人乐，阳荣昌，陈俊岭. 本征正交分解法在风电机组风场模拟中的应用[J]. 太阳能学报, 2014,35(9): 1764-1770.

MA Ren-le, YANG Rong-chang, CHEN Jun-ling. Application of proper orthogonal decomposition method in wind field simulation for wind turbine system[J]. ACTA Energiae Solaris Sinica, 2014, 35(9):1764-1770. (In Chinese)

[17]Measurement and evaluation of the mechanical vibration of wind energy turbines and their components VDI 3834[S]. Düsseldorf: Verein Deutscher Ingenieure, 2009:8-12.

Integrated Simulation of Wind Turbine Based on Vector Form Intrinsic Finite Element

CHEN Jun-ling1†, YANG Rong-chang2, MA Ren-le1

(1. Dept of Structural Engineering, Tongji Univ, Shanghai 200092, China; 2.Tongji Architectural Design (Group) Co Ltd, Shanghai 200092, China)

Large wind turbine system is a periodic time-varying system with rigid-flexible coupling multi-bodies. The traditional finite element method cannot solve the singular stiffness matrix produced by the rotation of blades. However, the vector form intrinsic finite element method can effectively solve the geometric deformation of elastic continuum, the nonlinear or discrete constitutive model, the coupling motion of continuum and rigid body, and so on. In this study, a solver program of space beam elements was developed by the vector form intrinsic finite element method with MATLAB code, and verified by two typical examples where one is a cantilever method with a dynamic force acting at the end, and the other is an Euler beam rotating around a fixed axis. The integrated simulation of wind turbine system that consists of tower, rotor blades, and nacelle was then established, and its dynamic response of free vibration under parking was analyzed. The natural frequencies of the turbine system were obtained by modal parameter identification, and they agree well with the results obtained by traditional finite element method. Moreover, the weighted amplitude wave superposition method and proper orthogonal decomposition method as well as B-spline surface interpolation were employed to obtain the wind time series of wind turbine under the normal operation condition. The wind-induced dynamic response of wind turbine system was also calculated by vector form intrinsic finite element method. The results reflect the periodic influence of gravity on the internal forces of blades and the interaction between blades and the tower.

wind turbine; vector form intrinsic finite element; numerical simulation; operation condition; nonlinear analysis

1674-2974(2016)11-0141-08

2015-11-24

国家自然科学基金资助项目(51378381), National Natural Science Foundation of China(51378381)

陈俊岭(1974-)，女，河北景县人，同济大学副教授，工学博士†通讯联系人，E-mail:chenjl@tongji.edu.cn

TK83；O322

A