基于数据挖掘的东北华北MS≥5.0地震活动参数综合指标分析*
王 岩 曹凤娟 王 亮 张 博 翟丽娜
(中国沈阳110034辽宁省地震局)

基于数据挖掘的东北华北MS≥5.0地震活动参数综合指标分析*
王 岩*曹凤娟 王 亮 张 博 翟丽娜
(中国沈阳110034辽宁省地震局)
根据地震活动参数的数据特征, 以2013年内蒙古科尔沁MS5.3地震为例, 引入主成分分析和因子分析两种数据挖掘方法, 在信息损失尽可能少的条件下, 实现对参数变量的约简降维, 并提取综合指标W. 研究显示, 2013年科尔沁MS5.3地震前两年,W值变化显著. 在进一步的单因子分析中, 从综合后的参数变量信息中重新提取了具有物理意义的多个单因子综合指标, 消除了大量信息重叠所造成的不一致, 实现了对综合指标的细化分析. 在此基础上, 对东北华北29次MS≥5.0地震的11个地震活动参数(频次N,b值,η值,A(b)值,Mf值,AC值,C值,D值,E值,Rm值, 响应比Y)进行主成分分析, 其结果显示, 主成分综合指标W在震前1—2年均出现了明显的异常变化, 这充分说明综合指标W可以用作地震预报研究的综合异常参考判据.
地震活动参数 主成分分析 因子分析 综合指标
引言
地震活动参数是指地震活动性研究中经多年实践积累得到的与地震时、 空、 强以及地下介质变化等信息紧密相关的变化指标(国家地震局预测预防司, 1997; 中国地震局监测预报司, 2002). 常用的地震活动参数中:b值,η值和Mf值反映G-R关系拟合中的偏离信息,Rm值反映固体潮的调制作用,C值反映地震空间集中度, 响应比Y反映介质的稳定程度, 这些参数均与地震孕育地点的地下介质变化相关;D值和AC值分别反映地震在时间分布上的丛集程度和演化特征; 能量E, 频度N和A(b)值则反映地震强度信息(陆远忠等, 1999; 华爱军等, 2001; 韩渭宾, 2003; 中国地震局监测预报司, 2007). 运用不同的地震活动参数能够从不同侧面挖掘震前震后的异常变化信息, 但由于参数自身固有的特性, 在实际应用过程中也常常出现异常特征不同步、 不一致的现象(王炜等, 2006a, b; 李永振, 2011), 难以判定震情趋势. 对众多地震活动参数的分析结果(韩渭宾, 2003)显示, 虽然不同参数所反映的地震活动性特征的角度不同, 但大都存在一定的相关性. 综合众多参数信息, 统一不同参数的判定结果, 是目前亟需解决的问题. 鉴于此, 本文拟引入主成分分析和因子分析两种数据挖掘方法(Hotelling, 1933; Gunopulos, Das, 2001; Moghad-dam, 2002), 将众多参数变量降维归纳为少数几个弱相关的综合变量, 以达到重复信息约简、 综合指标提取分析过程简化的目的(王岩等, 2016).
1 主成分分析与因子分析
为避免遗漏重要信息, 研究中通常会分析尽可能多的指标, 这在保证信息完整的同时却增加了分析问题的复杂性, 而且也会造成大量信息的重叠. 通过主成分分析法和因子分析法可将具有错综复杂关系的变量归结为少数几个综合因子.
1.1 主成分分析法
主成分分析法是通过正交变换将一组可能存在相关性的变量(指标)转换为一组线性不相关的新变量(综合指标)的数学降维方法.
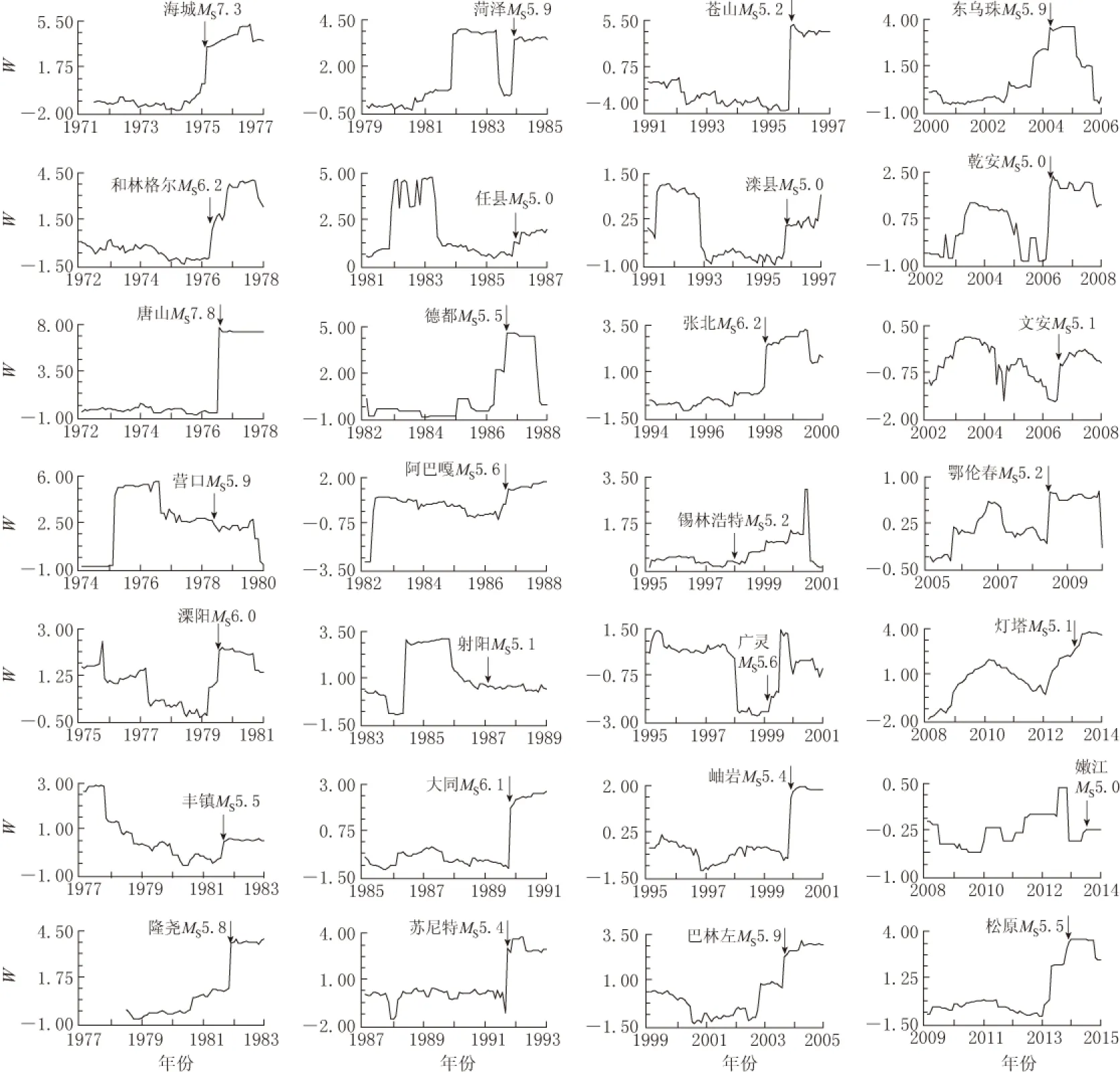
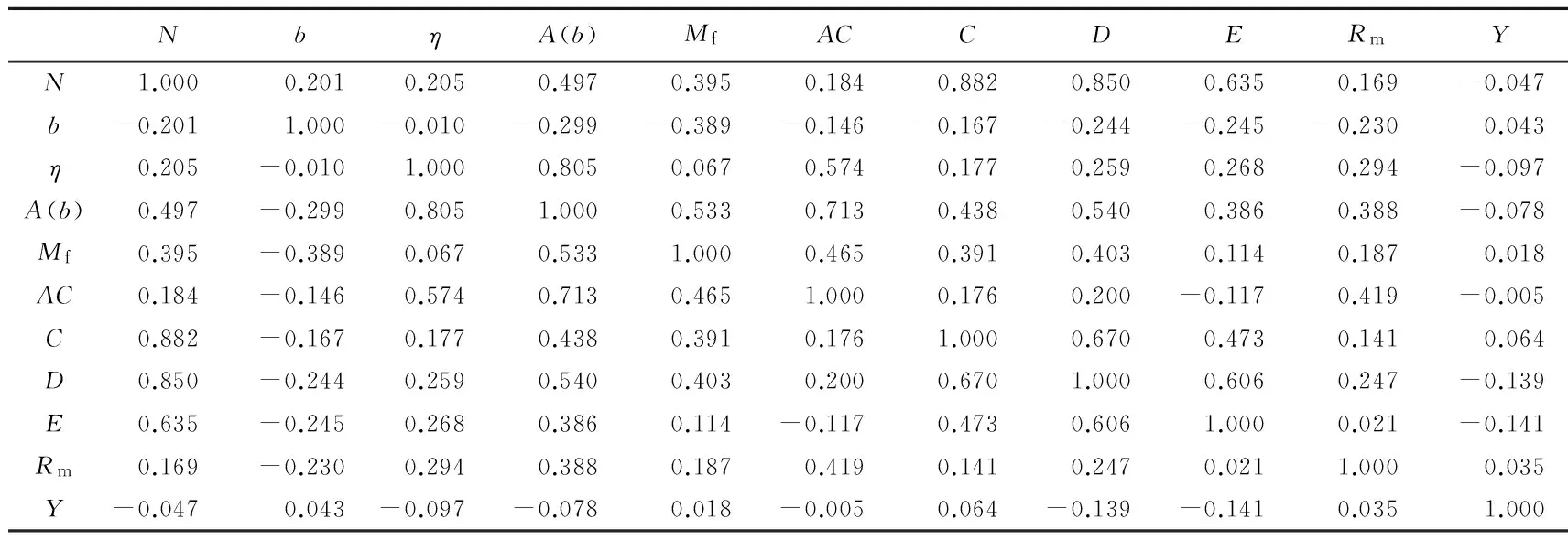
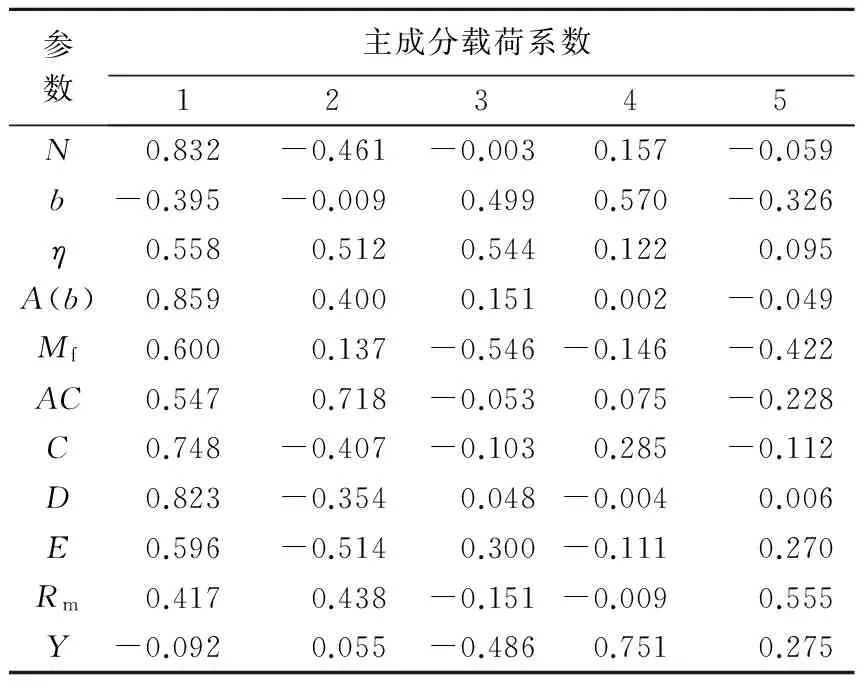
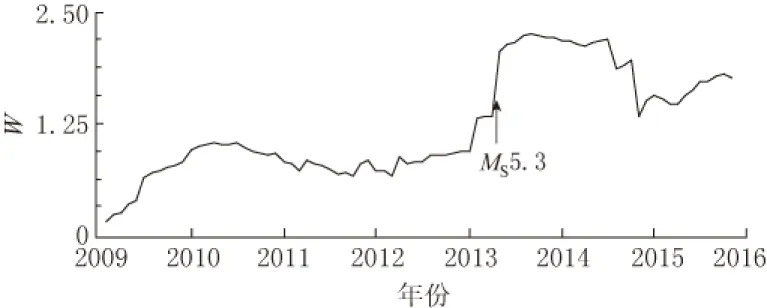
设xi(i= 1, 2, …,p)为地震活动参数变量, 进行主成分分析后得到的主成分Zi(i=1, 2, …,m且m (1) 该指标是能够反映地震时、 空、 强和地下介质异常的综合判定指标. 1.2 因子分析法 因子分析法是主成分分析法的发展, 其关键在于正交因子模型的建立和应用. 地震活动参数正交因子模型的建立如下: 存在m(m≤p)个公共因子fi(i= 1, 2, …,m), 使参数变量xi可用其线性组合表示为 (2) 式中: X=(x1, x2, …, xp)T; F为公共因子, F=(f1, f2, …, fm)T; ε为误差或特殊因子, ε=(ε1, ε2, …, εp)T; A为因子载荷矩阵A=(aij)p×m, 其中aij为第i个指标在第j个公共因子上的载荷, 是第i个变量与第j个公共因子的相关系数; 特殊因子εi相互独立, 且服从正态分布N(0, σ2). 设原始数据矩阵为 这里n为样本数, p为变量数. 由式(2)可以得到初始因子载荷矩阵A.A中通常有一些变量在几个公共因子上均有较大载荷, 使得初始公共因子的物理意义难以得到合理解释, 这时可旋转载荷矩阵A, 用一个正交阵右乘, 使旋转后的因子载荷阵结构简化, 便于对公共因子进行解释. 结构简化就是使每个变量仅在一个公共因子上有较大的载荷, 这种变换因子载荷的方法称为因子旋转. 基于主成分分析的过程, 根据各公共因子得分fi和相应的权值(贡献率)ei, 因子分析的综合指标为 (3) 将多参数中的信息合并后按照类别再分类, 可用单因子综合指标表示为 (4) 与主成分综合指标相比, 单因子综合指标可以根据需求进行因子筛选, 且筛选后所提取的单因子综合指标能够更细化地表现多类别的特征. 2.1 地震活动参数分析 以2013年4月22日内蒙古科尔沁MS5.3地震为例, 计算得到地震发生前后震中周围200 km范围内的11个地震活动性参数(频次N,b值,η值,A(b)值,Mf值,AC值,C值,D值,E值,Rm值, 响应比Y)随时间的变化曲线, 如图1所示. 参数计算震级为ML2.5—6.0, 累计时间为18个月, 滑动步长为1个月. 从该图中可见, 不同参数在地震发生前变化规律明显不一致. 图1 2013年科尔沁MS5.3地震11个地震活动参数的变化曲线 对选取的11个参数进行线性相关性计算, 结果列于表1, 表中相关系数的数值大小代表相关性强弱, 正负代表相关方向. 可以看出, 除响应比Y与各参数的相关性较弱外, 其余各参数之间均存在较强的相关性. 其中: 频次N,C值,D值, 能量E等4个与地震强度相关性较大的参数之间的相关性相对更强;η值,A(b)值,AC值,Rm值等4个与地震发生地地下介质变化相关较大的参数之间的相关性相对更高. 表1 2013年科尔沁MS5.3地震11个活动性参数的相关性系数 进一步检验可知: 参数变量数据KMO(Kaiser-Meyer-Olkin)检验(Kaiser, 1960; Hill, 2011)的统计量结果为0.663, 说明各参数之间的相关性较强; Bartlett’s球型检验(Bartlett, 1937)的相伴概率P值小于设定显著性水平0.05, 独立性假设不成立, 也说明各参数之间存在相关性, 即研究震例的地震活动参数作为变量符合主成分分析法和因子分析法对数据的要求. 2.2 主成分分析 科尔沁地震活动参数主成分分析中的成分特征值、 贡献率和主成分累计贡献率列于表2, 可见少数几个主成分中已经涵盖了大部分的参数信息. 参数变量主成分载荷矩阵列于表3, 可以看出表中与其它参数相关性较弱的响应比Y在对不同主成分的影响程度上是反向增加的, 但其在选取5个主成分的情况下, 仍能发挥较大作用, 说明主成分综合分析中的信息涵盖是全面的. 表2 2013年科尔沁MS5.3地震活动参数主成分特征值和贡献率 Table 2 Eigenvalues and contribution rate of HorqinMS5.3 earthquake in 2013 表3 2013年科尔沁MS5.3地震活动参数主成分载荷系数 图2 2013年科尔沁MS5.3地震前后综合指标W的变化Fig.2 Variation of the comprehensive index W before and after 2013 Horqin MS5.3 earthquake 选用5个主成分, 在信息涵盖率高于85%的情况下, 计算科尔沁地震发生前后的综合指标W, 得到W随时间变化的曲线, 如图2所示. 可以看出, 在地震发生前两年, 综合指标有明显的异常变化. 表4 2013年科尔沁MS5.3地震因子载荷系数 2.3 因子分析 为了进一步解析综合指数的异常变化, 在主成分分析的基础上, 对参数变量矩阵进行旋转, 重新整合信息, 得到因子载荷矩阵, 如表4所示. 与表3中主成分载荷对比可知, 经过旋转的因子对不同变量的敏感度发生了变化, 在承载多参数统计意义信息的同时, 较好地表达出了综合信息单因子的不同物理倾向. 因子分析将单一参数的载荷尽可能集中于单一因子上, 在表达统计意义的基础上, 更便于不同因子物理意义的解释. 其中: 因子1对频次N,C值,D值和能量E这4个与地震强度相关较大的参数更为敏感; 因子2对η值,A(b)值,AC值和Rm值这4个与地震发生地地下介质变化相关较大的参数更为敏感; 因子3受到b值和Mf值不同方向的较大程度影响, 也与介质变化特征相关; 因子4则受到响应比Y的影响最大, 变化趋势与响应比单参数变化相似. 选择4个因子计算单因子综合指标Wfai的结果如图3所示, 可以看出不同单因子综合指标的变化规律均有其自身的特点. 与地震强度相关的Wfa1在地震发生前两年开始有显著变化; 与地下介质变化相关的Wfa2和Wfa3则从地震发生前4年开始有变化; 由于因子4受到响应比Y的影响很大,Wfa4的变化规律与图1中响应比Y的变化类似. 单因子综合指标排除了信息重叠对分析结果可靠性的影响, 同时实现了信息最小完整集内特征的合理分类. 不同单因子综合指数的时间变化规律, 代表了不同物理特征的先后变化规律, 符合地震孕育发生过程中由介质变化、 能量聚集及地震强度所反映的普遍特征. 图3 2013年科尔沁MS5.3地震单因子综合指标Wfai的变化曲线 为了进一步对综合指标方法的区域可用性展开分析, 在典型震例的研究基础上, 本文对1970年以来东北华北地区(34—55°N, 110—135°E)地震目录中较为完整的28次中强震进行了11个地震活动参数(地震频次N,b值,η值,A(b)值,Mf值,AC值,C值,D值,Rm值, 能量E, 响应比Y)的主成分分析. 参数计算中, 按照地震孕育过程的可能影响范围, 取以震中为圆心的圆域(MS5.0—5.4, 半径为200 km;MS5.5—5.9, 半径为250 km;MS6.0—7.0, 半径为300 km;MS≥7.0, 半径为350 km), 选取ML≥2.5地震序列, 以窗长1.5年、 步长1个月进行计算. 图4给出了28次中强震前后主成分综合指标W随时间的变化曲线, 可以看出, 在地震发生前1—2年, 综合指标W均有显著的变化. 发生在郯庐断裂带的1975年海城MS7.3, 1978年营口MS5.9, 1995年苍山MS5.2, 1999年岫岩MS5.4, 2013年灯塔MS5.1这5次地震前1—2年综合指标W均呈明显下降的特征; 发生在张渤断裂带的1978年唐山MS7.8, 1995年滦县MS5.0和1998年张北MS6.2地震前1—2年, 综合指标W均呈升高与降低交替出现的特征, 且震后W呈快速上升; 发生在山西断裂带的1981年丰镇MS5.5, 1989年大同MS6.1, 1998年张北MS6.2和1999年广灵MS5.6这4次地震中, 丰镇地震与广灵地震的综合指标特征相似, 即震前1—2年综合指标W呈显著下降, 而大同地震和发生在张渤断裂带、 山西断裂带交界处的张北地震则与张渤断裂带地震的特征相似. 由此说明, 不同断裂带地区地震综合指标的特征具有一定的固有特色, 主成分载荷变化特征也较为相似, 这与所选地震活动参数中包含反映地下介质信息的参数有关. 传统的地震活动参数大都具有明确的物理意义, 包含着丰富多样的信息, 但由于数据信息大量重叠、 分析手段单一、 交互综合复杂等问题, 其在应用上颇为受限. 主成分分析和因子分析两种数据挖掘方法, 依据不同参数本身的特点及其相互关系, 对信息进行重新整合, 完成了参数的降维, 简化了多参数变量的分析过程, 合理地避免了信息矛盾问题, 实现了融合信息特征的再提取. 1970年以来, 东北华北的29次MS≥5.0地震的综合指数W分析结果表明, 综合指标在地震发生前均有明显的前兆变化. 通常在地震发生前的1—2年内, 综合指数均有下降再上升的趋势变化, 且发震震级越大, 影响时段越长, 变化程度越显著, 这一变化特征可以作为地震预报研究中的判据. 进一步对单因子综合指标Wfai分析, 从参数变量统计学变换中挖掘合理的物理解释, 在综合指标约简降维的同时, 细化了地震异常分析, 使综合指数的应用更为广泛. 图4 东北华北28次MS≥5.0地震综合指标W的变化曲线 国家地震局预测预防司. 1997. 测震学分析预报方法[M]. 北京: 地震出版社: 49--116. Department of Prediction and Prevention, State Seismological Bureau. 1997.AnalysisandPredictionMethodsofSeismometry[M]. Beijing: Seismological Press: 49--116 (in Chinese). 韩渭宾. 2003. 地震活动性参数分类及其相关性初步研究[J]. 四川地震, (3): 1--5. Han W B. 2003. Primary study on the classifying among the seismicity parameters and their correlativity[J].EarthquakeResearchinSichuan, (3): 1--5 (in Chinese). 华爱军, 刘西林, 刁守中, 李红. 2001. 华北地区中等、 大地震前算法复杂性AC值异常变化特征[J]. 内陆地震, 15(4): 326--330. Hua A J, Liu X L, Diao S Z, Li H. 2001. Abnormal characteristics of arithmetic complexityACvalue before moderate, strong earthquakes in North China[J].InlandEarthquake, 15(4): 326--330 (in Chinese). 李永振. 2011. 主成分分析法在辽宁地区地震预测中的应用[J]. 西北地震学报, 33(1): 76--79. Li Y Z. 2011. Application of primary components analysis method to earthquake prediction in Liaoning Province[J].NorthwesternSeismologicalJournal, 33(1): 76--79 (in Chinese). 陆远忠, 阎利军, 郭若眉. 1999. 用于中短期地震预报的一些地震活动性参量相关性讨论[J]. 地震, 19(1): 11--18. Lu Y Z, Yan L J, Guo R M. 1999. Discussion about correlation of some seismological parameters in medium- and short-term earthquake prediction[J].Earthquake, 19(1): 11--18 (in Chinese). 王炜, 林命週, 赵利飞, 马钦忠. 2006a. 地震活动参数约简的因子分析方法[J]. 西北地震学报, 28(4): 303--308. Wang W, Lin M Z, Zhao L F, Ma Q Z. 2006a. Factor analysis method for reducing seismicity parameters[J].NorthwesternSeismologicalJournal, 28(4): 303--308 (in Chinese). 王炜, 刘悦, 李国正, 吴耿锋, 马钦忠, 赵利飞, 林命週. 2006b. 我国大陆强震预测的支持向量机方法[J]. 地震学报, 28(1): 29--36. Wang W, Liu Y, Li G Z, Wu G F, Ma Q Z, Zhao L F, Lin M Z. 2006b. Support Vector Machine method for forecasting future strong earthquakes in Chinese mainland[J].ActaSeismologicaSinica, 28(1): 29--36 (in Chinese). 王岩, 邵媛媛, 曹凤娟, 郭晓燕. 2016. 基于因子分析的地震综合指数在辽宁地区地震预测中的应用[J]. 防灾减灾学报, 32(1): 1--7. Wang Y, Shao Y Y, Cao F J, Guo X Y. 2016. Application of comprehensive index to earthquake prediction of Liaoning using factor analysis method[J].JournalofDisasterPreventionandReduction, 32(1): 1--7 (in Chinese). 中国地震局监测预报司. 2002. 强地震中短期预报方法及其效能研究[M]. 北京: 地震出版社: 45--87. Department of Monitoring and Prediction, China Earthquake Administration. 2002.StudyonMedium-andShort-TermForecastMethodsandTheirEfficiency[M]. Beijing: Seismological Press: 45--87 (in Chinese). 中国地震局监测预报司. 2007. 中国大陆地震序列研究[M]. 北京: 地震出版社: 20--24. Department of Monitoring and Prediction, China Earthquake Administration. 2007.ResearchesonEarthquakeSequencesofChineseMainland[M]. Beijing: Seismological Press: 20--24 (in Chinese). Bartlett M S. 1937. Properties of sufficiency and statistical tests[J].ProcRSocA, 160(901): 268--282. Gunopulos D, Das G. 2001. Time series similarity measures and time series indexing[J].AcmSigmodRecord, 31(2): 624. Hill B D. 2011.TheSequentialKaiser-Meyer-OlkinProcedureasanAlternativeforDeterminingtheNumberofFactorsinCommon-FactorAnalysis:AMonteCarloSimulation[D]. Stillwater, Oklahoma State: Oklahoma State University: 40--43. Hotelling H. 1933. Analysis of a complex of statistical variables into principal components[J].JEducPsychol, 24(6): 417--441. Kaiser H F. 1960. The application of electronic computers to factor analysis[J].EducPsycholMeasur, 20(1): 141--151. Moghaddam B. 2002. Principal manifolds and probabilistic subspaces for visual recognition[J].IEEETransPatternAnalMachIntell, 24(6): 780--788. Comprehensive index analyses on seismic activity parameters based on data mining forMS≥5.0 earthquakes in northeast China and North China Wang Yan*Cao Fengjuan Wang Liang Zhang Bo Zhai Lina (EarthquakeAdministrationofLiaoningProvince,Shenyang110034,China) According to the data characteristics of seismic activity parameters, taking theMS5.3 Horqin, Inner Mongolia earthquake in 2013 for a typical case, the present paper introduces principal component analysis method and factor analysis method to reduce the dimension of parameter variables on the condition of information loss as little as possible, and extracts the comprehensive index. The result shows that the comprehensive indexWhad been changed significantly two years before the earthquake. Furthermore, by conducting factor analysis on Horqin earthquake, several single factor comprehensive indices with physical meanings are extracted, not only eliminating the inconsistency caused by the overlapping of information, but also achieving the refinement of the comprehensive index. In further research, the principal component analysis result about the eleven seismic activity parameters (N,b,η,A(b),Mf,AC,C,D,E,Rm,Y) of 29 earthquakes withMS≥5.0 in northeast China and North China shows that comprehensive indexWof principal component analysis had obvious precursor changes in 1—2 years before the earthquakes. This suggests that the index W can be taken as a precursory in earthquake prediction research. seismic activity parameters; principal component analysis; factor analysis; comprehensive index 辽宁省地震局专项项目(LZ-201606)和震情跟踪定向工作任务(2015010112)共同资助. 2016-01-15收到初稿, 2016-07-01决定采用修改稿. 10.11939/jass.2016.06.010 P315.5 A 王岩, 曹凤娟, 王亮, 张博, 翟丽娜. 2016. 基于数据挖掘的东北华北MS≥5.0地震活动参数综合指标分析. 地震学报, 38(6): 906--913. doi:10.11939/jass.2016.06.010. Wang Y, Cao F J, Wang L, Zhang B, Zhai L N. 2016. Comprehensive index analyses on seismic activity parameters based on data mining forMS≥5.0 earthquakes in northeast China and North China.ActaSeismologicaSinica, 38(6): 906--913. doi:10.11939/jass.2016.06.010. *通讯作者 e-mail: wangyancau@126.com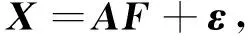
2 2013年科尔沁MS5.3地震综合指标分析



3 东北华北中强震综合指标分析
4 讨论与结论