双极性锌银贮备电池优化设计的可靠性研究

冯秀丽， 原勇强， 李必进， 崔益秀

(中国工程物理研究院电子工程研究所，四川绵阳621900)

双极性锌银贮备电池优化设计的可靠性研究

冯秀丽， 原勇强， 李必进， 崔益秀

(中国工程物理研究院电子工程研究所，四川绵阳621900)

围绕双极性锌银贮备电池低温脉冲负载能力不足的问题，开展了双极性锌银贮备电池的优化设计，提出了两套设计方案,同时对两套优化方案获得的低温放电数据进行了系统讨论。结果显示在显著性水平为0.01时,根据GB/T4882-2001中夏皮洛-威尔克检验方法验证两套设计方案获得的放电数据均为正态分布的;采用GJB/T376-87中计量数据估计可靠度的方法得出方案B具有较高的可靠性。最后筛选出方案B为双极性锌银贮备电池的优化方案。

双极性锌银电池；贮备电池,优化设计；可靠性评估；正态性检验

双极性锌银贮备电池[1]属于一次电池，干态贮存，使用时借助气体发生器产生高压推动电解液进入电堆体，激活电池进入工作状态。它的独特之处[2]在于由一片正单极、若干个双极性片和一片负单极按次序堆叠形成电堆且共用1个进液通道，这使得双极性锌银贮备电池多为贫液设计，从而降低电池内部短路的概率。正是这种贫液设计，容易引发双极性锌银贮备电池在激活过程时出现电解液在电堆体内分布不均匀的现象，导致电池内阻升高，低温脉冲负载能力不足。因此解决双极性锌银贮备低温负载能力的有效途径——提高电解液用量。但是电解液量提高多少是一个值得研究的问题。

目前,双极性锌银贮备电池可靠性验证方案没有国家标准可依据。鉴于双极性锌银贮备电池是一次产品，激活性能直接影响电池的工作性能，而火工品的发火性能直接决定电池激活性能，为此借鉴GJB 376火工品可靠性评估方法完成双极性锌银贮备电池工作可靠性的评估[3-4]。在样本量少的情况下，采用计数数据评估可靠度会导致评估结果过于保守，而采用计量数据评估可靠度是一个不错的选择[5]。

本文针对双极性锌银贮备电池低温脉冲负载能力不足，提出了增加电解液用量的两套优化方案。按两套优化方案分别生产15组电池，在低温环境下放电，收集电池脉冲负载电压。根据GB/T4882-2001中夏皮洛-威尔克检验方法[6]，在一定的显著性水平下，对方案A和方案B收集的放电数据的正态性做出判断，再根据GJB/T 376-87中计量数据估计可靠度的方法，对两套电池优化方案可靠性做出评估，筛选出双极性锌银贮备电池的优化方案。同时本文的研究结果将为一次性贮备电池的可靠性评估提供一些思路。

1　双极性锌银贮备电池的优化方案

针对贫液设计的双极性锌银贮备电池在低温环境下脉冲负载能力不足的问题，提出了增加电解液用量的两套优化方案。方案A为在原电池电解液体积的基础上增加8%，电池的其他组件不变；方案B为在原电池电解液体积的基础上增加12%，电池的其他组件不变。按上述两套方案分别组装15只双极性锌银贮备电池。

2　放电数据的收集与正态性的判断

2.1数据收集

将30只双极性锌银贮备电池放在10℃环境下保温4 h，然后按一定的技术要求放电，记录电池在5C倍率下的最低放电电压，结果见表1。

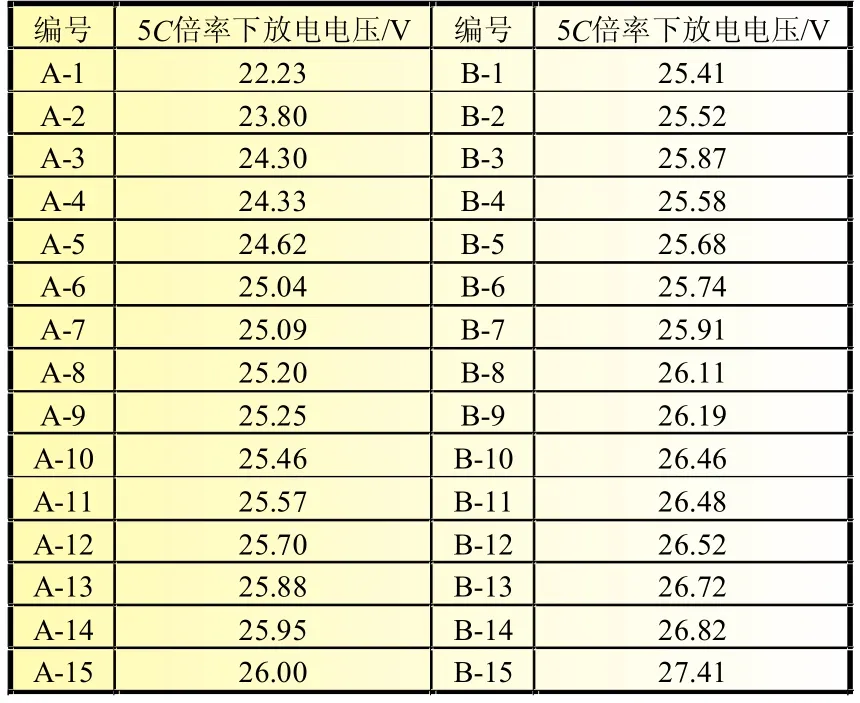
表1　低温环境下优化后电池5C倍率放电电压

2.2数据评估

2.2.1评估方法的介绍

夏皮洛-威尔克检验是基于次序统计量对它们期望值的回归，是一个完全样本的方差分析形式的检验。检验统计量(W)为样本次序统计量线形组合的平方(S2)与通常的方差估计值(nm2)的比值。在显著性水平a=p的情况下，从GB/T4882-2001表11查得样本量为n，p=a情况下的p分位数Wp。如果计算统计量W值小于Wp，则拒绝零假设，即数据是非正态分布的；否则接受零假设，即数据是正态分布的。本检验方法涉及的数学公式见(1)～(4)。

公式(1)为样本算数均值的数学表达形式:

公式(2)为夏皮洛-威尔克检验的辅助量S的数学表达形式:

式中：S为夏皮洛-威尔克检验的辅助量；ak为夏皮洛-威尔克检验的系数；x(n+1－k)为按非降次序排列的样本中，样本的第(n+1－k)个值；xk为按非降次序排列的样本中，样本的第k个值；n为样本量；k为按非降次序排列的样本内，观察值x的个数；当n为偶数，k取值范围为[1，n/2]，当n为奇数时，k取值范围为[1，(n－1)/2]。

公式(3)为方差估计值nm2的数学表达形式:

式中：nm2为方差估计值；xi为按非降次序排列的样本中，样本的第i个值；为算数平均值。

公式(4)为检验统计量的数学表达形式：

式中：W为检验统计量；S2为夏皮洛-威尔克检验的辅助量的平方；nm2为方差估计值。

显著性水平[7]是指在零假设为真的情况下，假设检验这种方法犯第一类错误的概率。本文设定显著性水平为0.01，样本量n=15，a=p=0.01，p的分位数Wp=0.835时，讨论Wp与计算所得的W值间关系，从而对两种方案中放电数据的正态性做出判断。

2.2.2方案A放电数据的正态性的判断

从表1可知，方案A共有15个独立放电数据并按升序排列。根据公式(1)，方案A获得的放电数据的算数均值为24.961 33 V。在方案A中n=15，k=7，从GB/T4882-2001表10中查得a1～a7数据值,具体情况见表2。

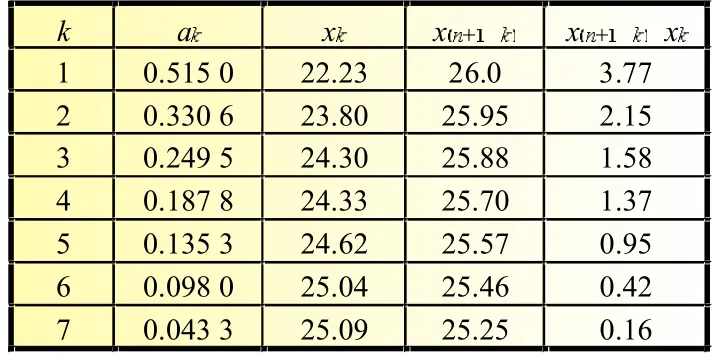
表2　方案A电池放电数据收集与处理结果

根据表2中数据，通过公式(2)～(4)，计算得出方案A中S=3.480 41，nm2=13.989 37，W=0.865 9。由于计算得到的W值(0.865 9)大于Wp值(0.835)，所以在显著性水平为0.01时不拒绝零假设，方案A获得的放电数据是正态分布的。

2.2.3方案B放电数据的正态性的判断

从表1可知，方案B共有15个独立放电数据并按升序排列。根据公式(1)，方案B获得的放电数据的算数均值为26.141 33 V。在方案B中n=15，k=7，从GB/T4882-2001表10中查得a1～a7数据值,具体情况见表3。

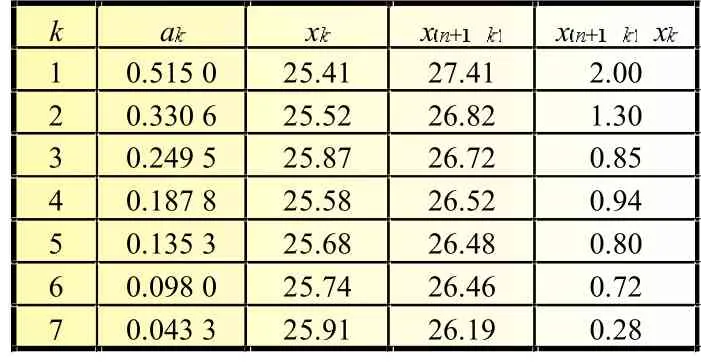
表3　方案B电池放电数据收集与处理结果

根据表3中数据，通过公式(2)～(4)，计算出方案B中的S=2.114 077，nm2=4.757 773，W=0.93。由于计算得到的W值(0.939)大于Wp值(0.835)，所以在显著性水平为0.01时不拒绝零假设，方案B获得的放电数据是正态分布的。

3　优化方案的可靠性评估

3.1评估方法的介绍

从本文第二部分可知，采用夏皮洛-威尔克检验方法，在显著性水平为0.01时方案A和方案B获得的放电数据服从正态分布，可用正态统计容许限计算可靠度。本文讨论的双极性锌银贮备电池5C放电电压的容许上限Lu为29.7 V，容许下限Ll为24.3 V。根据公式(5)～(7),计算出正态容许限系数Ku和Kl。

查GJB376-1987附表C(P110页)，得出在Ku、n=15、r=0.80的条件下可靠度Ru及在Kl、n=15、r=0.80的条件下可靠度RL，最后根据公式(8)计算出优化方案中锌银贮备电池的可靠度。

公式(5)是样本观测值标准偏差的数学表达式：

式中：σ为标准偏差；nm2为方差估计值。

公式(6)是正态容许限系数Ku数学表达式：

式中:Ku为正态容许限系数；Lu为电压容许上限；为算数平均值；σ为标准偏差。

公式(7)是正态容许限系数Lu数学表达式：

式中：Lu为正态容许限系数；Ll为电压容许下限；为算数平均值；σ为标准偏差。

公式(8)是可靠度数学表达式：

式中：R为电池可靠度；Rl为容许下限可靠度；Ru为容许上限可靠度。

3.2方案A的可靠性评估

方案A优化后的双极性锌银贮备电池5C放电电压的算术均值为24.96，标准偏差σ为0.999 6，容许上限Lu为29.7 V，容许下限Ll为24.3 V。根据公式(5)～(7),计算出方案A放电数据正态容许上限系数Ku=4.74，正态容许下限系数Kl=0.66。查GJB376-1987附表C(P110页)，得出在Ku=4.74、n=15、r= 0.80的条件下可靠度Ru为0.999 95；Kl=0.66、n=15、r=0.80的条件下可靠度RL＜0.762 1，最后根据公式(8)计算方案A中优化后的锌银贮备电池的可靠度小于0.762 0。

3.3方案B的可靠性评估

通过方案B优化后的双极性锌银贮备电池5C放电电压的算术均值为26.14，标准偏差σ为0.582 9，容许上限Lu为29.7 V，容许下限Ll为24.3 V。根据公式(5)～(7),计算出方案A放电数据正态容许上限系数Ku=6.10，正态容许下限系数Kl=3.15。查GJB376-1987附表C(P110页)，得出在Ku=6.10、n=15、r=0.80的条件下可靠度Ru为1.0；Kl=3.15、n=15、r=0.80的条件下可靠度RL为0.994 43，最后根据公式(8)计算-方案A中优化后的锌银贮备电池的可靠度为0.994 43。

4　结论

通过对双极性锌银贮备电池两套优化方案的研究，得出结论如下：

(1)在显著性水平0.01时，方案A和方案B获得的双极性锌银贮备电池低温5C放电数据均是正态分布的；

(2)在置信度为0.80时，方案A设计的双极性锌银贮备电池的可靠性小于0.762 0；方案B设计的双极性锌银贮备电池的可靠度为0.994 43；

(3)在原电池电解液体积的基础上增加12%的优化方案B可提高双极性锌银贮备电池的低温脉冲负载能力，是较优的优化方案。

[1]杨希仁.双极性锌银贮备电池组电解液分配系统的研究[J].电源技术,1998,22(6):224-246,249.

[2]冯秀丽,崔益秀,原勇强.双极性锌银贮备电池失效分析[C]//2015年全国金相检测及失效分析技术交流会论文集.青岛：2015年全国金相检测及失效分析技术交流会，2015：99-101.

[3]高艳,刘合财,龚敏庆.热电池的可靠性模型[J].贵阳学院学报，2010，5(3)：52-54.

[4]梁凤岗，常赟.热电池可靠性验证方案探讨[J].电源技术，2002，26(2)：95-97.

[5]国防科学技术工业委员会.GJB 376火工品可靠性评估方法[S].北京：国防科学技术工业委员会，1987.

[6]国家质量技术监督局.GB/T4882-2001数据的统计处理于解释正态性检验[S].北京：国家质量技术监督局，2001.

[7]张小天.显著性水平的含义[J].社会学研究，1997(2)：31-36.

Reliability research on optimal design of bipolar silver-zinc reserve battery

FENG Xiu-li,YUAN Yong-qiang,LI Bi-jin,CUI Yi-xiu
(China Academy of Engineering Physics,Mianyang Sichuan 621900,China)

The bipolar silver-zinc reserve batteries are deficient in impulsive load volt at the lower temperature.To solve this problem,two pieces of optimal design were presented and two sets of discharge data from optimal design at the lower temperature were obtained.The normality and reliability of discharge data from optimal designs were discussed systematically.The normality of discharge data was tested according to Shapiro-Wilk inspection method from GB/T4882-2001 at the remarkable level of 0.01.It is concluded that discharge data from optimal designs are normal.According to measurement data assessment method from GJB/T376-87,reliability assessment of optimal designs were conducted and design B possessed higher reliability.Thus design B was screened as the optimal design.

bipolar silver-zinc battery;reserve battery;optimal design;reliability assessment;normality tests

TM 911

A

1002-087 X(2016)10-2002-02

2016-03-18

冯秀丽(1977—)，女，辽宁省人，副研究员,博士，主要研究方向为电池设计。