考虑多因素的电网关键线路主客观综合辨识模型
陈卉灿, 栗然, 吕子遇, 翟晨曦, 李永彬
(1.广东电网有限责任公司电力调度控制中心, 广东 广州 510600;2.新能源电力系统国家重点实验室(华北电力大学), 河北 保定 071003)
考虑多因素的电网关键线路主客观综合辨识模型
陈卉灿1, 栗然2, 吕子遇2, 翟晨曦2, 李永彬2
(1.广东电网有限责任公司电力调度控制中心, 广东 广州 510600;2.新能源电力系统国家重点实验室(华北电力大学), 河北 保定 071003)
提出考虑多因素的电网关键线路主客观综合辨识方法——从电网拓扑结构以及运行状态角度出发,建立子指标体系,针对以往研究没有深入考虑各个子指标在关键线路辨识过程中地位和作用的问题,利用层次分析法确定各子指标主观权重,利用熵权法确定客观权重,在综合考察主客观权重的基础上,构建关键线路的综合辨识指标。最后利用IEEE 39节点系统为例进行分析,与研究成果进行比较,说明该方法的合理性和可靠性。
复杂网络理论;电网运行状态;层次分析法;熵权法;关键线路辨识
为了适应国民经济的飞速发展,满足社会日益增长的电力需求,电网规模不断扩大,在一定程度上降低了电网的安全稳定性能。近年来频发的大面积停电事故就是电网安全问题。这些大停电事故一般都是由薄弱环节触发的连锁故障引起。因此,采用合理的方法对电网关键线路进行辨识,对及早发现潜在危险、维护社会利益,具有重大的现实意义。
目前,已有很多学者展开了对电网关键线路辨识的研究,并且取得了一定成果。基于电力网络的复杂网络理论具有无标度特性以及小世界特性[1-2],从拓扑结构角度进行关键线路的辨识具有明显的优势。文献[3]将发电机出力作为权重,定义了带权重线路的介数指标,并将线路介数值提高到其相邻线路的指标最高值进行修正,辨识处于电网关键位置的线路。文献[4]利用电抗作为权重,提出了电抗加权介数的概念,用于关键线路的辨识。文献[5]利用节点的运行容量以及运行极限对电抗介数进行修正,根据运行情况修改电抗参数。此外,还有一些文献从电网运行角度,采用电力系统分析方法进行关键线路辨识。文献[6]从潮流流动角度,提出潮流分布熵和潮流转移熵的概念,从冲击和后果辨识关键线路。文献[7]除了利用潮流熵指标之外,还通过求取节点电压偏移、节点重要度指标,构建评价关键线路的综合指标。
以上文献评价指标各有侧重,考虑因素比较单一。为了提高关键线路辨识结果的准确性,综合考虑电网拓扑结构和运行状态成为今后研究的重点。文献[8]基于复杂网络理论,结合功率输送关系,定义功率介数指标进行关键线路的辨识。并利用效能函数验证结果的合理性。文献[9]综合考虑继电保护的影响、节点电压偏移、拓扑结构以及潮流分布等因素,提出了综合介数指标,对电网的关键线路进行辨识。文献虽然综合考虑拓扑结构以及运行状态,但大部分只是将这些因素进行相对简单的组合,并没有考虑各个指标之间的相对重要程度,只是简单地人为赋予权重,并没有深入研究挖掘。
本文提出一种综合考虑拓扑结构以及运行状态的带权重的关键线路辨识方法。首先引入基于电抗的加权介数指标、基于节点度数的联系度指标以及基于有功功率状态重要度指标3个子指标,然后分别采用层次分析法、熵权法确定3个指标的主观权重和客观权重,根据决策者对主客观的需求程度,构建关键线路的综合辨识指标。最后以IEEE 39节点系统为例,进行关键线路的辨识,并通过与已有文献的研究成果进行比较,说明本文方法的可行性以及可靠性。
1 关键线路辨识指标
1.1 基于电抗的加权介数指标
在复杂网络理论中,边介数定义为边被所有节点对的最短路径经过的次数[10],即
(1)
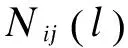
介数作为一种辨识关键环节的常用工具,经常应用于一些无权无向网络中,直接将其应用于复杂电网关键线路的搜寻,势必存在较大的误差。因此,有必要针对电网特点对传统介数进行修正。
电网的主要功能就是将能量从发电机节点输送至负荷节点。忽略线路损耗,有功功率的简化计算公式[4]为
(2)
式中:Pij为线路ij流过的有功功率;ui、uj为节点i、j的电压;αij为节点i和节点j的电压相位差;xij为线路ij的电抗。
由式(2)可知,线路传输的有功功率与线路电抗存在着反比关系。在功率的诸多传输路径中,电抗值小的路径承担着较大的功率传输任务。
结合复杂网络理论中介数的定义以及电力系统的特点,文献[4]重新定义了最短路径的概念:电源节点到负荷节点的所有路径中,线路电抗和最小路径为该发电-负荷节点对的最短路径。线路被所有最短路径经过的次数定义为基于电抗的加权介数。
基于电抗的加权介数,不仅考虑了各个线路的差异,反映电网的拓扑结构,而且一定程度上反映了潮流流动的物理规律。断开线路的电抗介数越高,切断的功率传输路径越多,网络平均路径长度增加的越多,造成的后果越严重。相对于传统的介数指标,能够更好的识别电网关键线路。
1.2 基于节点度数的联系度指标
在复杂网络理论中,节点度数定义为与节点相连的线路数量之和[11]。节点的度数反映了节点之间联系的紧密程度。节点度数越大,与外界信息交换越频繁,在拓扑结构中的位置越重要。
网络平均度数指各个节点度数的平均值,计算公式为
(3)
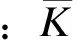
电网中难免出现电抗介数相同的线路,为了更好从结构上辨识电网的关键线路,借鉴文献[11]利用节点度数来计算线路关键指标的思想,定义线路的联系度指标
(4)
Sl描述了线路与外界联系的紧密程度,线路两端节点度数越大,则与该线路相连的线路数越多,其所处的位置也就越关键。
综上所述,基于电抗的加权介数指标Bl和基于节点度数的联系度Sl共同从拓扑结构角度为关键线路的辨识提供了思路,但各自的侧重点有所不同:Bl在考虑了潮流流动物理规律的基础上,注重的是边(线路)在整个网络中信息传输(电能)的作用;Sl侧重衡量边(线路)之间联系的紧密程度。
1.3 基于有功功率的状态重要度指标
电网关键线路的识别要综合考虑电网拓扑结构以及电网运行状态,为此,提出基于有功功率的状态重要度指标
(5)
式中:Cij为线路ij的状态重要度指标;Pij为线路ij流过的有功功率;Rij为线路ij的有功功率裕度;Pijmax为线路ij的有功功率极限。
基于有功功率的状态重要度指标,从电网运行角度为关键线路的辨识提供了思路。一方面,实时运行中,线路的主要功能就是传输有功功率,因此有功功率越大的线路,其承担的任务越重,在电网中越关键;另一方面,从故障后果角度而言。线路流过的有功功率越大,其因故障或者蓄意攻击而断开后,其潮流转移量越大,可能造成的后果越严重。此外,当存在线路切断潮流转移现象时,有功功率大,但裕度小的线路能够承载的潮流转移量越小,越有可能出现越限情况,造成进一步开断,继续引发潮流大规模转移,最终导致连锁故障的发生。
2 关键线路综合辨识指标
2.1 子指标归一化
文章第一节从拓扑结构、运行状态角度说明3个子指标在单位、数量级方面均存在差异。为了提高综合辨识指标的准确性,首先要将子指标分别进行归一化处理。
将基于电抗的加权介数指标归一化为
(6)
将基于节点度数的联系度指标归一化为
(7)
将基于有功功率的状态重要度指标归一化为
(8)
式中:Bl、Sl、Cl分别为3个子指标的原始计算结果;Bmin、Bmax、Smin、Smax、Cmin、Cmax分别为3个子指标计算结果的最小值和最大值。
2.2 基于层次分析法的主观综合指标
利用层次分析法[12](analytical hierarchy process, AHP)确定各个指标的权重,构建主观综合指标。层次结构模型共3层,如图1所示。

图1 层次结构模型

(9)
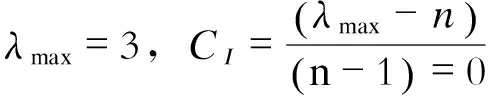
(10)
2.3 基于熵权法的客观综合指标
熵权法是一种简单的客观赋权方法,其基本思想是根据各评价指标所提供信息量的大小来确定指标权重[13]。
设归一化第j个指标Uj的熵为Hj,则
(11)
(12)
当fij=0,令fijlnfij=0。
式(11)-式(12)中:xij为第i个对象的第j个归一化指标值;n为对象个数。
利用熵的概念计算指标i权重公式为
(13)
针对某指标而言,各个对象的指标值差异越小,其熵值越大,则熵权值越小。尤其当各个对象具有相同指标值时,熵值为1,权值为0。因此,熵权法充分挖掘了已有数据提供的信息,更加注重对象之间的差异性,差异性越大的指标辨识对象的能力必然越强。
利用熵权值以及归一化的子指标构建客观综合指标
(14)
V2l构建了关键线路的综合辨识指标
(15)
式中:a、b分别为主客观指标的权重,根据具体情况进行取值。
Vl为决策者根据实际需求制定相关权重提供了一定空间,避免辨识过于主观;另一方面,利用熵权法充分挖掘了已有的数据信息,辨识结果更加合理。
3 算例分析
3.1 算例基本信息
本文以IEEE 39节点系统为例,其拓扑结构如图2所示。该系统共有10台发电机、19个负荷节点和46条线路。按照文献[14]提供的思路为各条线路配置最大有功传输容量。

图2 IEEE 39节点系统图
3.2 关键线路辨识
a) 首先计算各条线路基于电抗的加权介数指标Bl、基于节点度数的联系度指标Sl、基于有功功率的状态重要度指标Cl。
b) 根据求得的指标值,利用熵权法求出权重,得到客观综合指标
(16)
由层次分析法得到的主观综合指标
(17)
根据决策者对主客观的需求程度,对参数a、b赋予不同的取值,不同的取值会影响线路综合辨识指标的计算结果。本文均衡看待主客观权重的影响,令a=0.5,b=0.5得到关键线路的综合辨识指标
(18)
IEEE 39节点系统各条线路的综合辨识指标计算结果如图3所示。
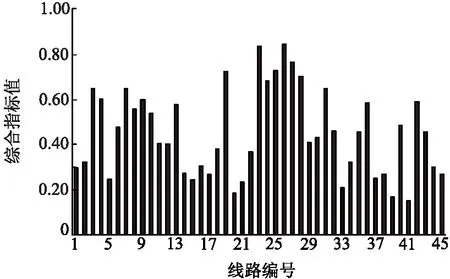
图3 关键线路综合辨识指标结果
由图3可以发现,综合辨识指标值呈现明显的分级现象。只有少数线路的指标值较高,属于关键线路:指标值超过0.8的线路有2条;超过0.7的线路有 6 条;大部分线路的指标值相对较低,集中在0.40~0.20之间。这与实际情况是一致的,少数的关键线路对电网的安全运行起着至关重要的作用,它们一旦故障,将大大影响系统的正常运行,甚至造成系统解列。
按本文方法选取综合指标排在前10位的线路,并将结果与已有模型进行对比,结果见表1。其中,文献[3]采用带权重的线路介数法进行辨识,文献[15]利用效用风险熵进行关键线路的辨识。
表1 关键线路辨识结果对比

排名综合指标值本文方法文献[3]文献[15]10.845845L16-17(26)L15-16(25)L16-19(27)20.836036L13-14(23)L16-17(26)L14-15(24)30.765401L16-19(27)L16-19(27)L15-16(25)40.729838L15-16(25)L16-21(28)L13-14(23)50.724684L10-13(19)L16-24(29)L2-3(3)60.703895L16-21(28)L17-18(30)L16-24(29)70.681861L14-15(24)L17-27(31)L4-5(8)80.649183L3-18(7)L2-25(4)L16-17(26)90.648068L17-27(31)L2-3(3)L5-6(10)100.647431L2-3(3)L1-2(1)L26-28(43)
注:括号内为线路编号;下标为2个节点间的线路编号。
从表1可知道,利用3种方法得到的前10位关键线路中有1/2以上数的相同线路。说明本文方法的可行性和可靠性,但排序结果不同以及其他关键线路辨识结果的差异是由于考察指标的侧重点不同而导致的。
从电网结构角度出发,线路第L15-16以及L16-17的基于电抗的加权介数指标在所有线路中是最大的。由图2也可以发现,这两条线路属于重要的联络通道,它们一旦故障将造成系统解列成两个子系统,削弱了系统之间的联系,影响发电机组的功率外送,造成部分区域的供给不足,大大增加了系统瘫痪的可能性及其后果,文献[3]可证实。
L14-15在本文以及文献[15]中视为关键线路。文献[15]指出线路L14-15断开,将导致潮流大范围转移,降低系统的均衡性,这在文献[6]也得到证实,文献[3]的方法更关注拓扑结构,并没有将此线路视为关键线路。
L17-27传输的有功功率较小,按照文献[15]的方法,不属于关键线路,但从电网拓扑结构角度而言,若其发生故障,会影响发电机37、38的功率外送[16],文献[3]也证明了这一点。此外,该线路的裕度较小,但其他线路故障造成潮流转移时,L17-27很容易发生过载,引发连锁故障。因此本文将L17-27识别为关键线路。
通过以上分析可以发现,本文提出主客观综合辨识指标综合考虑了电网拓扑结构以及运行状态,能够较好辨识电网关键线路。
4 结束语
本文提出了一套考虑多因素的电网关键线路主客观综合辨识方法。从电网拓扑结构以及运行状态角度出发,提出了基于电抗的加权介数指标、基于节点度数的联系度指标、基于有功功率的状态重要度指标。为了更好衡量各个子指标在辨识过程中的相对重要程度,利用层次分析法确定主观权重,利用熵权法确定客观权重。在综合考量主客观权重的基础上,构建了关键线路的综合辨识指标。最后利用IEEE 39节点系统为例进行了分析,通过与已有的研究成果进行比较,说明了方法的合理性以及可靠性。
但本文考察的因素还不够完善,将电压等级、故障引起的风险等因素纳入其中,构建一套完善的关键线路辨识方法,是今后工作的重点。
[1] WATTS D J.Small Worlds:The Dynamics of Networks Between Order and Randomness[M].USA:Princeton University Press, 1998.
[2] CHASSIN D P, PROSSE C.Evaluating North American Electric Grid Reliability Using the Barabasi-albert Network Model[J].Physic A, 2005, 355(2/4):667-677.
[3] 曹一家, 陈晓刚, 孙可.基于复杂网络理论的大型电力系统脆弱线路辨识[J].电力自动化设备, 2006, 26(12):1-5.
CAO Yijia, CHEN Xiaogang, SUN Ke.Identification of Vulnerable Lines in Power Grid Based on Complex Network Theory[J].Electric Power Automation Equipment, 2006, 26(12):1-5.[4] 刘耀年, 术茜, 康科飞, 等.基于电抗加权介数指标的电网脆弱线路辨识[J].电力系统保护与控制, 2011, 39(23):89-92.
LIU Yaonian, SHU Xi, KANG Kefei, et al.Identification of Vulnerable Lines in Power Grid Based on the Weighted Reactance Betweenness Index[J].Power System Protection and Control, 2011, 39(23):89-92.
[5] 丁明, 韩平平.加权拓扑模型下的小世界电网脆弱性评估[J].中国电机工程学报, 2008, 28(10):20-25.
DING Ming, HAN Pingping.Vulnerability Assessment to Small-world Power Grid Based on Weighted Topological Model[J].Proceedings of the CSEE, 2008, 28(10):20-25.[6] 李勇, 刘俊勇, 刘晓宇, 等.基于潮流熵的电网连锁故障传播元件的脆弱性评估[J].电力系统自动化, 2012, 36(19):11-16.
LI Yong, LIU Junyong, LIU Xiaoyu, et al.Vulnerability Assessment in Power Grid Cascading Failures Based on Entropy of Power Flow[J].Automation of Electric Power Systems, 2012, 36(19):11-16.
[7] 蔡晔, 曹一家, 李勇, 等.考虑电压等级和运行状态的电网脆弱线路辨识[J].中国电机工程学报, 2014, 34(13):2124-2131.
CAI Ye, CAO Yijia, LI Yong, et al.Identification of Vulnerable Lines in Urban Power Grid Based on Voltage Grade and Running State[J].Proceedings of the CSEE, 2014, 34(13):2124-2131.
[8] 王涛, 高成彬, 顾雪平, 等.基于功率介数的电网关键环节辨识[J].电网技术, 2014, 38(7):1907-1913.
WANG Tao, GAO Chengbin, GU Xueping, et al.Power Betweenness Based Identification[J].Power System Technology, 2014, 38(7):1907-1913.
[9] 刘小丽, 毛弋, 梁杉, 等.基于综合介数的电网脆弱线路辨识[J].电力系统保护与控制, 2016, 44(2):116-121.
LIU Xiaoli, MAO Yi, LIANG Shan, et al.Identification of Vulnerable Lines in Power Grid Based on Comprehensive Betweenness Index[J].Power System Protection and Control, 2016, 44(2):116-121.
[10] 汪小帆.复杂网络理论及其应用[M].北京:清华大学出版社, 2006.
[11] 刘耀年, 何俊, 曲晓, 等.基于关键性指标的电网脆弱线路辨识[J].电测与仪表, 2012, 49(10):42-45.
LIU Yaonian, HE Jun, QU Xiao, et al.Critical Indicator in Vulnerable Line Identification in Power System[J].Electrical Measurement & Instrumentation, 2012, 49(10):42-45.
[12] 王莲芬, 徐树柏.层次分析法引论[M].北京:中国人民大学出版社, 1990.
[13] 吴明, 富鑫, 刘广鑫.基于熵权法的天然气供需关系综合评价[J].当代化工, 2016, 45(1):92-95.
WU Ming, FU Xin, LIU Guangxin.Evaluation of the Relationship Between Supply and Demand of Natural Gas Based on Entropy-right Method[J].Contemporary Chemical Industry, 2016, 45(1):92-95.
[14] 鞠文云.基于复杂网络理论的电力系统脆弱元件辨识指标研究[D].武汉:华中科技大学, 2013.
[15] 丁明, 过羿, 张晶晶.基于效用风险熵的复杂电网连锁故障脆弱性辨识[J].电力系统自动化, 2013, 37(17):52-57.
DING Ming, GUO Yi, ZHANG Jingjing.Vulnerability Identification for Cascading Failures of Complex Power Grid Based on Effect Risk Entropy[J].Automation of Electric Power Systems, 2013, 37(17):52-57.
[16] 鞠文云, 李银红.基于最大流传输贡献度的电力网关键线路和节点辨识[J].电力系统自动化, 2012, 36(9):6-12.
JU Wenyun, LI Yinhong.Identification of Critical Lines and Nodes in Power Grid Based on Maximum Flow[J].Automation of Electric Power Systems, 2012, 36(9):6-12.
栗然 (1965),女,河北保定人。教授,工学博士,主要研究方向为新能源与并网技术,电力系统分析、运行与控制。
吕子遇 (1992),男,河北保定人,在读硕士研究生,主要研究方向为新能源与并网技术,电力系统分析、运行与控制。
(编辑 王夏慧)
Subjective and Objective Comprehensive Identification Model for Power Grid Critical Lines Considering Multiple Factors
CHEN Huican1, LI Ran2, LÜ Ziyu2, ZHAI Chenxi2, LI Yongbin2
(1.Guangdong Power Grid Power Dispatching Control Center, Guangzhou, Guangdong 510600, China; 2.State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Baoding, Hebei 071003, China)
This paperpresents a subjective and objective comprehensive identification method for power grid critical lines considering multiple factors which is to establish a sub-index system based on power grid topology structure and operational state.In allusion to the problem of past research not considering position and function of each sub-index in identifying critical lines, it uses analytical hierarchy process (AHP) to determine subjective weight of each sub-index and entropy-right method to confirm objective weight.On the basis of comprehensively investigating subjective and objective weight, it constructs comprehensive identification index for critical lines.By taking IEEE39 node system for an example, it analyzes and compares research results, and proves reasonability and reliability of this method.
complex network theory; power grid operational state; analytical hierarchy process; entropy-right method; critical line
2016-05-16
2016-07-16
广东电网有限责任公司重点规划专题资助项目(036000QQ00150002)
10.3969/j.issn.1007-290X.2016.11.019
TM614
A
1007-290X(2016)11-0100-05
陈卉灿(1989),女,湖北赤壁人。助理工程师,工学硕士,主要从事电力系统分析与控制等方面的工作。

