一种新型灰色绝对关联度在结构损伤识别中的应用

杨泽众

华北水利水电大学（450045）

一种新型灰色绝对关联度在结构损伤识别中的应用

杨泽众

华北水利水电大学（450045）

基于一种新的灰色绝对关联度来研究结构损伤识别问题。结果表明，这种方法可以准确快速地定性出结构的损伤程度大小，符合实际情况。

结构损伤；灰色理论；绝对关联度；数值模拟

0 引言

工程结构在施工以及使用过程中，由于构件的质量缺陷、荷载的作用以及环境的侵蚀等方面的影响，通常会出现不同程度的损伤。结构的损伤实际上是结构性态的改变，损伤识别就是要根据结构性态的变化去判断结构损伤的情况[1]。由于结构损伤程度的大小与各振动参数之间很难建立确定的数学关系，因此，结构的损伤识别问题可以视为灰色系统问题。当结构的某一位置发生损伤时，通过计算结构在损伤前后静态参数的关联度来分析判断结构的损伤程度。

1 灰色关联度理论

1.1 灰色绝对关联度模型

在灰色系统理论中，灰色关联度分析是很重要的一部分。灰色关联度分析的基本思想是根据数据序列所形成的曲线,比较其几何形状的相似程度，来判断出联系的紧密性。用灰色关联度来描述这种相似程度[2]。曲线几何形状接近，数据序列之间的关联度较大，反之则较小。

进行灰色关联度分析时，首先应当确定参考数列，然后将其他数列与参考数列进行比较，分析其接近程度，作出判断。灰色关联度的计算方法为：

首先，定义参考数列X0={x0(k){k=1,2,…,n}

定义比较数列Xi={xi(k){k=1,2,…,n}(i=1,2,…,m)

定义关联系数X0（k）与Xi（k）的关联系数为：

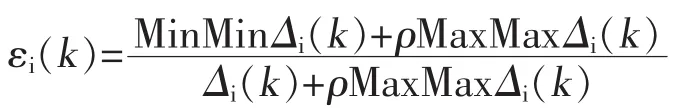
式中，△i（k）表示第k时刻X0（k）与Xi（k）的绝对差，△i(k)=x0（k）-xi（k）；Min△i（k）表示第一级最小差，MinMin△i（k）表示两级最小差，即在第一级最小差Min△i（k）的基础上，按i=1，2，…，m找出最小差中的最小差；Max△i（k）与MaxMax△i（k）同理。

综合各点的关联系数,得到整个xi曲线与参考曲线x0的关联度ri为：

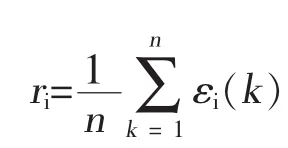
灰色绝对关联度[3]的计算：

关联系数：

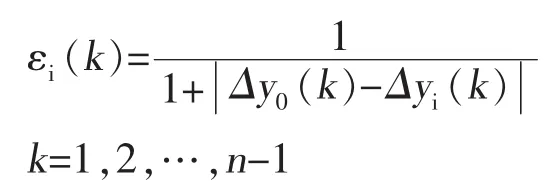
关联度：

1.2 新的灰色绝对关联度模型

灰色关联度理论基本思想是根据序列曲线几何形状来判断不同序列之间的联系是否紧密。但是当两个序列存在负相关关系时,按照传统算法计算，关联度是大于零的，说明其之间存在相似的发展关系，与实际情况相矛盾。为了克服关联模型的不足，本文采用一种拓展型的灰色绝对关联度模型[4]。

首先，定义定义参考数列X0=｛x0(1),x0(2,)…,x0(n)｝

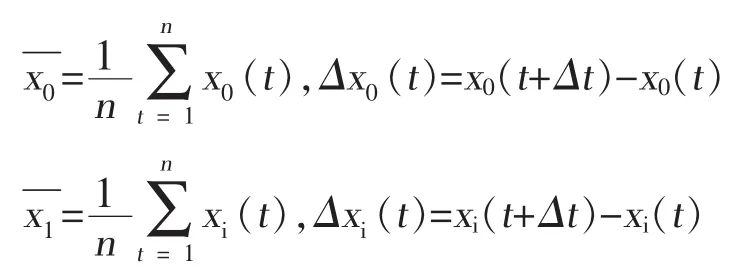
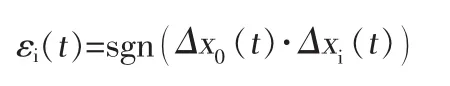
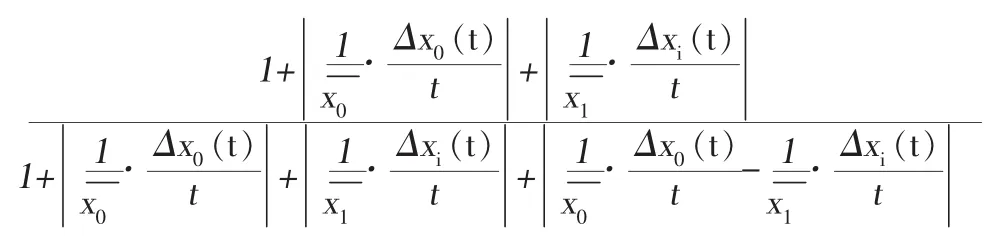
为关联符号函数。在实际中，大部分都是离散的数据，这里t取离散的数，即t=2…n，而△t=1，i= 1,2…m，εi（t）称为灰色绝对关联系数，εi称为X0与Xi的灰色绝对关联度，如下式所示：

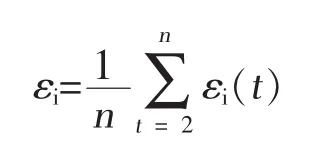
结构损伤的产生会导致结构特征参数的改变。在特征参数中，频率的测量最为直接方便，因此，本文选用频率作为分析结构损伤的特征参数。

首先，利用有限元建立简支梁模型，计算得到完好的模态频率，作为参考数列。然后，通过数值模拟，利用计算元刚度的降低来模拟结构损伤，作为比较数列。得到参考数列与比较数列后，计算关联数列和关联度，并根据关联度的大小，来判断结构的损伤程度。

根据灰色系统理论，若一个待识别结构的因素变量所示的曲线几何形状与完好结构的因素变量所示的曲线几何形状关联程度越小，则说明结构发生损伤的概率越大。

2 模型示例

如图1建立简支梁模型。简支梁的尺寸为：梁长700 mm，梁宽15 mm，梁高40 mm，弹性模量为2.06×1011Pa,泊松比为0.25,质量密度为7500 kg/m3。

图1 简支梁模型

通过有限元软件ANSYS计算出完好模型的前五阶频率，作为参考数列。得到如下数据：

然后通过计算元刚度的降低来模拟结构发生了损伤。损伤分三种情况，分别为：第5单元刚度损伤10%（工况一）；第5单元刚度损伤15%（工况二）；第5单元刚度损伤30%（工况三）。同样通过有限元软件来计算出前五阶模态频率，作为对比数列。得到如下数据：

通过本文介绍的新型灰色绝对关联系数的计算方法，计算得出如下结果：

所以三种工况的新型绝对关联度分别为：

通过以上的计算结果可以得出，第一种工况的关联度最大，其结构因素变量的曲线几何形状与完好结构因素变量的曲线几何形状关联程度也越大，说明其损伤程度最小；工况二次之，工况三的关联度最小，说明其损伤程度最大。以上结论与所建模型情况相符合。

当关联度接近于1的时候，说明对比数列与参照数列较接近。本文所设的三种工况损伤程度都不大，所以关联度都比较接近。但是通过本文介绍的新型绝对关联度的计算方法，仍然可以判断出三种工况的损伤程度大小，并与实际相符合，说明本文介绍的方法合理实用。

3 结语

文章通过对灰色关联度理论进行研究，结合传统灰色绝对关联度理论的特点，利用一种新型的灰色绝对关联度理论进行结构损伤识别问题的分析。通过ANSYS有限元软件建立模型,分三种损伤情况进行了数值分析，结果表明新型的灰色绝对关联度理论可以有效地进行结构损伤识别。

[1]黄天立.结构系统和损伤识别的若干方法研究[D].上海：同济大学，2007.

[2]刘思峰，党耀国，方志耕.灰色系统理论及其应用]M].北京：科学出版社，2005.

[3]梅振国.灰色绝对关联度及其计算方法[J].系统工程,1992, 10（5）.

[4]刘勇,刘思峰,Jeffrey Forrest.一种新的灰色绝对关联度模型及其应用[J].中国管理科学，2012,10(20).