对易拉罐的优化设计研究
向国锐
(成都七中实验中学,四川 成都 610000)
S1=πr2,S2=πr2,S3=2πrh
S=S1+S2+S3
S=2πr2+2πrh
minS=2πr2+2πrh
V2=V3=2πr2a
V材=V1+V2+V3=2πrha+8πra2+hπa2+4πa3+4πr2a
V材≈V=2πrha+4πr2a
minV=2ahπr+4aπr2
对易拉罐的优化设计研究
向国锐
(成都七中实验中学,四川 成都 610000)
本文考虑了生活中已知容积(体积)的易拉罐材料最省问题,在容积不变的情况下,分别讨论了易拉罐材料的表面积以及体检的最优模型。利用极值存在原理,通过求导数的方法,分别给出了在不同情形下的易拉罐最优设计,同时得到用料最少时罐体的高与半径的关系。
容积;设计;易拉罐
1 问题介绍
在生活中随处可见的如加多宝、王老吉、可口可乐等易拉罐饮料,如果我们仔细观察,发现他们的形状大小极其相似,皆大体是一个直圆柱形状。那么为何规格也极其相似,我将就此形状建立相应的数学模型来说明材料最省的规格,给出优化方案。
2 模型的建立与求解
2.1 易拉罐的体积测量
选啤酒罐(罐上标量355毫升)作为材料,测量其真实容积,为了避免一次测试造成的人为误差,多次测量并求平均值作为最终容积。
将啤酒罐装满水后倒入500毫升量筒内,平视液面凹处并读数。重复上述操作十次,记录每次的读数,数据如表1所示。算出十次测量的平均值作为最终容积。

表1 啤酒罐容积的10次测量数据
求十次测量平均值并作为真实体积,得到容积平均值为364.95毫升。为了便于计算,下面将罐体容积按V0=365毫升进行计算。
2.2 易拉罐模型的建立与求解
易拉罐的上下底面可近视为圆面,侧壁是平滑的柱形,其底面与侧壁连接处的卷边以及上底面的拉环等小技巧设计所用的材料统统忽略,即把该易拉罐形状假设为圆柱体,只考虑构成这圆柱体所用的材料,并以此建立模型求出最优时的解。
2.2.1 忽略厚度的圆柱体模型的建立与求解
假设圆柱体各个面的厚度相同,并将厚度忽略不计。此时,设圆柱体高为h,底面半径为r,表面积为S(如图1所示)。圆柱体表面积大小即所用材料多少。

图1 忽略壁面厚度的罐体圆柱体模型
设S1,S2代表上下底面面积,S3代表侧面面积,则有
S1=πr2,S2=πr2,S3=2πrh
因为圆柱体的表面积为上、下底面面积和侧面面积之和,即
S=S1+S2+S3
故有,
S=2πr2+2πrh
从而得到在容积一定的情况下,表面积的优化模型为
minS=2πr2+2πrh
(1)
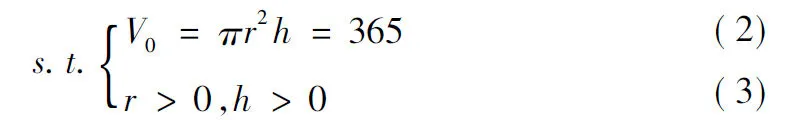
为了求解上述优化模型,先从(2)式中求得
(4)
将(4)式带入(1)式中,得
(5)
解得
(6)
将r的取值带入(4)式,得到
(7)

2.2.2 计入圆柱体厚度的模型建立与求解
在实际中圆柱体各面厚度并不相同,上下两底面厚度基本相同且大于侧壁的厚度,通过对易拉罐的实际测量,管壁厚度约为0.1毫米,罐盖和罐底的厚度是其他部分厚度的2倍左右。设侧壁厚度为a,上下两底面厚度为2a。圆柱体内部空间高为h,圆柱体内半径为r,易拉罐所用材料体积为V材(如图2所示),易拉罐所用材料的体积V材大小即材料的用量。

图2 考虑壁面厚度的罐体圆柱体模型
V1代表考虑厚度后易拉罐侧壁的材料体积,V2,V3分别代表罐顶盖和罐低的材料体积,则有
V1=[π(r+a)2-πr2](h+4a)=2πrha+8πra2+hπa2+4πa3
(8)
V2=V3=2πr2a
(9)
用,可得易拉罐所用材料的体积
V材=V1+V2+V3=2πrha+8πra2+hπa2+4πa3+4πr2a
(10)
因为壁面厚度a相对于罐体半径r很小,因此(10)中的含有a2,a3的项可以忽略,得到
V材≈V=2πrha+4πr2a
从而得到在容积一定的情况下,所用材料体积的优化模型为
minV=2ahπr+4aπr2
(11)

类似于模型(1),(2)和(3)的求解,从(12)中求得,
(14)
将(14)带入(11)中,并利用极值原理求解,得到方程
(15)
求解(15),得到
(16)
将(16)带入(14)可得
(17)
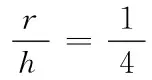
[1] 徐茂良,邓启良,刘睿,郑波.易拉罐形状和尺寸的最优设计模型[J].成都大学学报(自然科学版),2008,27(2):105-108
[2] 周文国.易拉罐的设计方案[J].中学数学教学,2002(1):12-12
[3] 王颖,王惠书.易拉罐的最优化问题[J].山西广播电视大学学报,2008,13(4):98-99
[4] 丁仕杰.《导数在生活中的优化问题举例》的教学和反思[J].吉林省教育学院学报旬刊,2013(11):36-37
[5] 裔晶晶,金健.易拉罐形状和尺寸的最优设计[J].常熟理工学院学报,2012(10):51-54
TH122
A
1671-1602(2016)20-0037-02

