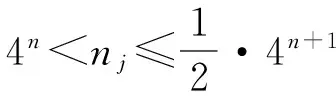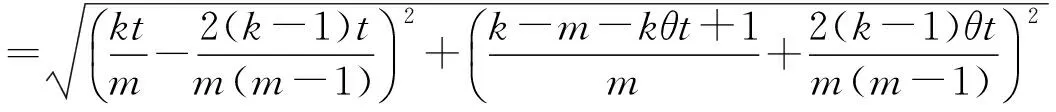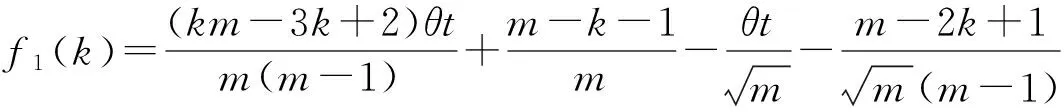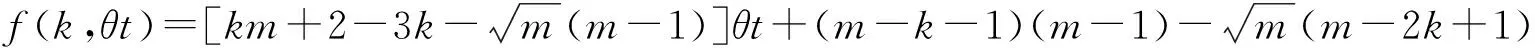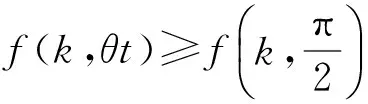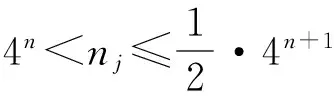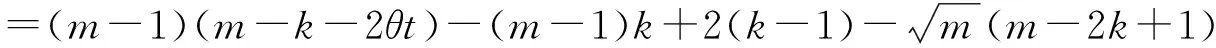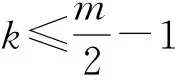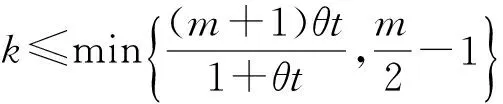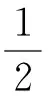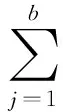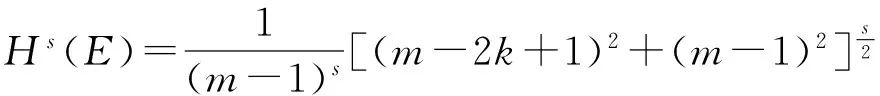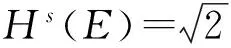含双参变量(θ,t)的广义Cantor尘的Hausdorff测度

金艳玲

(山西大学商务学院 基础教学部,山西 太原 030031)



含双参变量(θ,t)的广义Cantor尘的Hausdorff测度

金艳玲

(山西大学商务学院 基础教学部,山西 太原 030031)

研究在剪切和压缩变换作用下所得到的广义Cantor尘的Hausdorff测度问题．利用自然覆盖及图形的几何结构获得此类广义Cantor尘的Hausdorff测度精确计算公式．推广已有结论．

广义Cantor尘;Hausdorff测度;自相似集

自相似分形集的Hausdorff测度研究是分形几何中的一个困难问题．文献[1]对经典的分形集的Hausdorff测度的性质进行了讨论,文献[2,3]在经典Cantor集基础上通过单位正方形生成了Cantor集类,称为Cantor尘,讨论其性质,并得到一类Cantor尘的Hausdorff测度的计算公式,文献[4,5]则改变Cantor尘的生成方法,得到了另外一类Cantor尘的Hausdorff测度,文献[6]在[3]的基础上,加入了夹角变量,讨论了更广泛的Cantor尘的Hausdorff测度．本文则在[3]的基础上,研究在剪切和压缩变换作用下所得到的广义Cantor尘,即含双参变量的Cantor尘的Hausdorff测度精确计算公式．

1 图形的生成

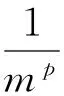
图1 含双参变量的广义Contor尘

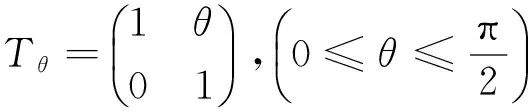
2 特殊点的坐标

为了讨论含双参变量(θ,t)的广义Cantor尘的Hausdorff测度,我们计算一些特殊点的坐标.

对于A点,讨论其坐标

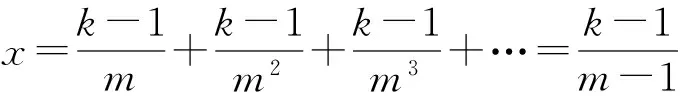
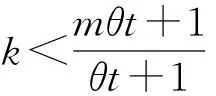
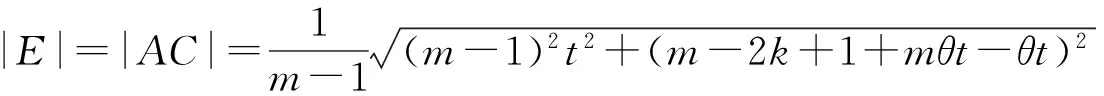
3 引理

引理1 如果开集U可以包含任意两个相邻两类的p级拷贝,则

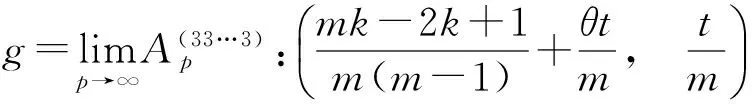
经过计算可知,|sl|>|gq|

引理2 如果U可以包含任意两个相对两类的p级拷贝,则

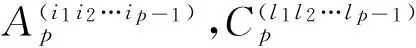
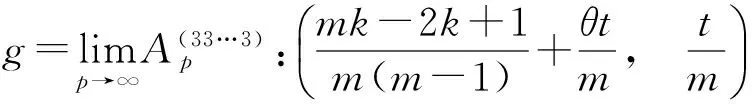
4 主要结论

定理1 设Uj是包含E的nj个p级拷贝的开集,则

其中s=logm4(m≥4)

证明:以下对p采用数学归纳法．

第一步:验证当p=1时,对nj=1,2,3,4都有结论成立．

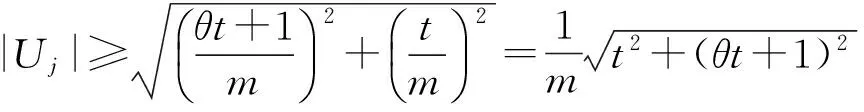
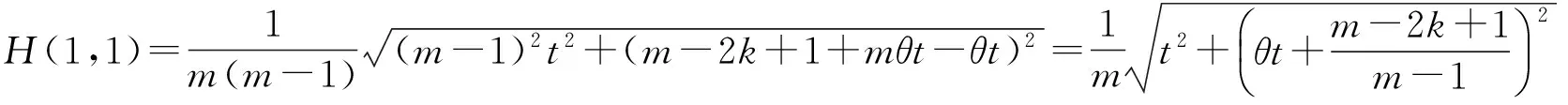
显然,|Uj|>H(1,1)

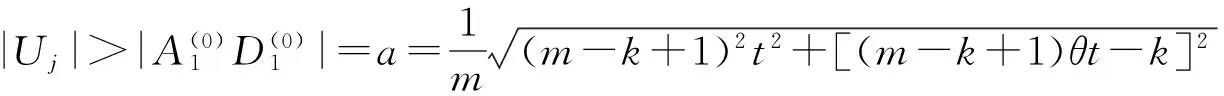
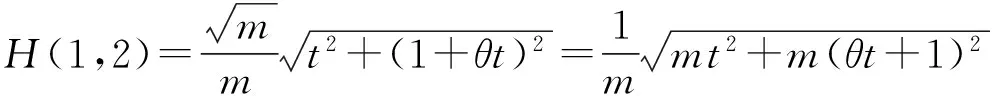
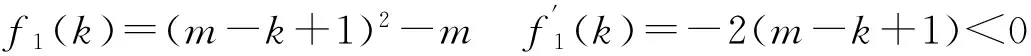
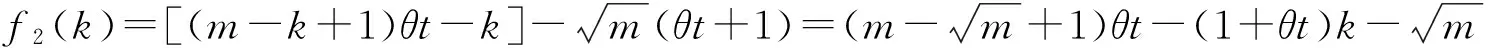
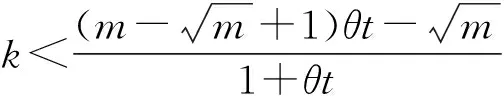
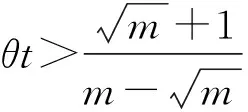
a≥H(1,2)⟹|Uj|≥H(1,2)

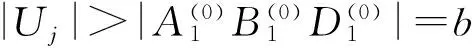
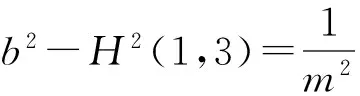
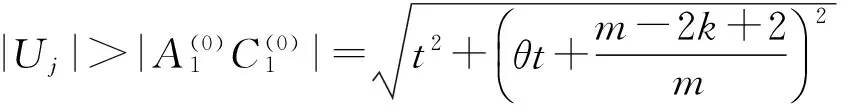
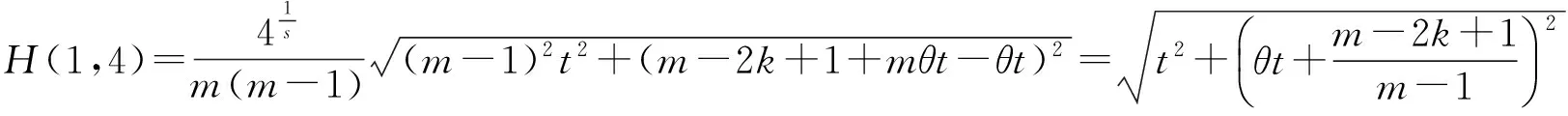
经过简单计算可得|Uj|≥H(1,4)

第二步:假设p=n时,有

以下证明p=n+1时,有

当1≤nj≤4n时,若Uj仅可包含nj个同类n+1级拷贝,则由归纳法可得

当4n

经计算,此项分子差小于f(k,θt).

故,|Uj|>c>H(n+1,nj)成立．

2) 若平面开集Uj可包含相对两类的n+1级拷贝,由引理2可得

定理2 设Hs(E)为含双参变量(θ,t)的广义Cantor尘E的Hausdorff测度,

证明:一方面,利用自然覆盖,由Hs(E)的定义有

故

特别地,

与已知结论均一致．

[1] 何伟弘,罗 俊,贾保国.Cantor尘和Sierpinski地毯[J].中山大学学报(自然科学版),1999,38(4):117-119

[2] 曾超益,许绍元.Cantor尘的Hausdorff 测度的初等证明[J].数学的实践与认识,2003,33(6):78-82

[3] 曾超益,袁德辉.m分Cantor尘的Hausdorff测度[J].纯粹数学与应用数学,2009,25(2):356-362

[4] 金艳玲,魏毅强.一类非齐次Moran集的Hausdorff测度[J].中北大学学报(自然科学版),2011,32(1):63-66

[5] 金艳玲.一类m分Cantor尘的Hausdorff测度[J].太原科技大学学报,2012,33(4):317-320

[6] 曾超益,袁德辉.含参变量Cantor集的Hausdorff测度[J].数学杂志,2011,31(4):729-736The Hausdorff Measure of a Class of Cantor Dust with Parameter(θ,t)

JIN Yanling

(Dept.Public Foundation,Business College of Shanxi University, Taiyuan 030031, China)

To sdudy the problem of the hausdorff measure of a class of cantor dust which is obtained by shear transformation and compressed transformation, using natural cover theory and its geometric construction,to obtain the exact value of the hausdorff measure of this set which is extention about this class of cantor dust.

generalized cantor dust; hausdorff measures; self-similar set

2016-08-17

山西大学商务学院科研基金项目(2014029).

金艳玲(1981-)，女，吉林通化人,硕士,山西大学商务学院讲师，主要从事分形几何研究.

1672-2027(2016)03-0001-05

O174.12

A