基于数据融合的公交客流规模测算方法

李林波，姜 屿，王 婧，吴 兵

(1.同济大学道路与交通工程教育部重点实验室，上海201804；2.济南市规划设计研究院，山东济南250101)

基于数据融合的公交客流规模测算方法

李林波1，姜 屿1，王 婧2，吴 兵1

(1.同济大学道路与交通工程教育部重点实验室，上海201804；2.济南市规划设计研究院，山东济南250101)

公交客流规模测算往往存在调查成本受限和准确度要求较高的矛盾。提出基于公交IC卡历史数据与人工补充调查数据的数据融合测算方法，以准确推算公交客流规模。首先根据公交线路的基本属性，采用聚类分析方法划分线路类型，从每一类中选择具有代表性的线路。基于IC卡数据分析公交客流时变特征，运用有序样本聚类Fisher算法将线路小时刷卡量进行聚类分析。划分刷卡量相似时段，进而采用优化方法确定调查抽样率，确定相应的调查车辆进行人工补充调查，最终经过数据融合计算获得公交客流规模。基于上海市某辖区IC卡数据进行案例分析，测算得到三类公交线路的日均客流量。

公共交通；客流规模；聚类分析；数据融合；公交IC卡；上海市

0 引言

优先发展公共交通往往需要通过财政扶持的形式激励公交企业提升服务质量，因此需要对公交线路的实际客流规模进行评估。目前，政府获取公交客流规模的主要方法有两种：1)利用公交企业年报，但由于企业数据管理不健全，导致年报数据往往存在很大的误差；2)利用公交IC卡(以下简称“IC卡”)数据，但是该数据只能反映持卡者的客流信息，无法反映总体公交客流情况，简单地使用IC卡刷卡比例推算总体客流情况也无法精准地反映公共交通的实际服务情况。人工调查方法是获取公交客流规模最为直接有效的方法，但由于调查费用太高而不现实。面对这一困境，基于IC卡客流数据，如何通过人工补充调查并采用数据融合技术对公交客流规模进行准确推算就显得很有意义。

随着信息技术的发展，越来越多的城市开始使用IC卡。各城市的IC卡系统发展的不统一导致信息研究方法的差异，主要包括上客车站判断[1-2]、下客车站判断[3-4]以及换乘判断[5-6]三个内容。文献[7]从数据管理、数据质量控制、数据分析与应用等方面详细阐述利用IC卡系统进行公交客流调查的方法。文献[8]对出行调查和IC卡信息利用进行对比分析，并探讨两者融合的可行性。文献[1]和文献[9]提出如何将IC卡记录的原始信息转化为可直接运用于城市交通规划及公交运营调度的基本信息。文献[10]对IC卡数据的采集方法和数据结构进行分析总结，确定IC卡数据分析的具体目标。这些研究成果为人工调查数据和IC卡数据的融合处理提供了借鉴。

本文提出一种公交客流规模测算方法，即通过分时段人工抽样调查实际公交客流情况，并基于数据融合理念对IC卡数据进行总体扩样。首先，考虑到调查成本的限制，将所有公交线路进行分类，选出可以代表该类型公交客流情况的公交线路。其次，分析公交客流的时变特征，提出线路小时刷卡量聚类分析方法，从调查成本和结果精度两方面，借鉴最优化思想提出调查最佳抽样率的计算方法，并根据IC卡数据分析所对应的刷卡时段，详细梳理公交线路的运营调度计划，确定具体被调查的公共汽车，制定调查方案。最后，基于数据融合理念对IC卡客流数据进行扩样分析，测算公交客流总体规模。

1 IC卡数据聚类分析

1.1 聚类分析方法的优势

在公交客流调查中，通过一条或几条线路调查获得的IC卡数据扩样系数，以此对所有线路的IC卡客流进行总体客流规模估计的方法存在以下问题：1)由于不同线路客流情况不一样，采用同样的扩样系数会造成较大误差；2)同一线路在一天中的客流也存在显著的时变特征，采用同一扩样系数会放大或缩小客流总体规模。当然，增加调查线路是提高数据准确度的有效方法，但在实际过程中，受限于成本投入，其可操作性不强。

通过对不同线路客流情况的观测发现，在公交线路走向、车型配置和运营方式等方面相似的线路，其客流特征具有相似性[11]。因此，可以考虑在进行公交客流规模测算时，先将线路进行聚类分析[10]，进而抽取每一类线路中的部分车辆为代表进行调查分析，最终获得反映该类线路的客流特征信息。这样可以有效减小不同线路采用相同扩样系数带来的误差，同时，对不同类型线路的具体划分可以提高数据的有效性和结果的准确性。

此外，由于居民出行会随时间呈现周期性变化，因而公交客流的总体特征也会呈现周变、日变和时变特性。通过对公交线路IC卡刷卡量的分析发现，任何公交线路的客流情况在某一时段里总是呈现相似的时变特征，主要表现为一天中各个小时的流量在某些相邻时段内IC卡刷卡量的相似性[11]。鉴于这种相对稳定的特征，可以根据现有的小样本数据将性质相似时段的IC卡数据进行归类分析，这种按照时间顺序来分析客流特征的过程在统计学中被归为有序样本聚类问题。

1.2 相似线路聚类分析

为了对数条信息完整的公交线路进行合理分类，需要选取聚类指标，聚类指标应能够比较客观、全面地反映每一类型线路刷卡量的变异特征。线路长度、车站数量为线路的自身属性，会直接影响公交运营的实际情况，进而影响整条线路的客流量级、客流构成和IC卡刷卡比例等。线路类型是规划者对公交线路属性的划分，不同类型线路的客流量及服务对象不同，每种交通对象群体都有不同的持卡比例，从而影响整条线路的刷卡情况。而平均发车间隔和线路拥挤程度则会影响乘客是否选择乘坐该线路，不同社会地位、经济条件对象的接受程度各不相同，进而反映的不同群体使用IC卡的比例也会相应受到影响[12]。

线路长度(LoR)、车站数量(NoBS)、线路类型(RT)、平均发车间隔(ADI)以及线路拥挤程度(CD)5个指标分别从总体、个体的角度影响线路的客流总量，能在一定程度上反映线路客流的变异性。因此，选择这五个指标作为公交线路的聚类属性构造样本矩阵，并利用SPSS18.0软件实现聚类过程。

1.3 相似小时聚类分析

相似小时聚类分析通常应用有序样本聚类Fisher算法[13-14]，可以有效划分公交客流的相似时段，对于抽样时间的选取具有重要的现实意义。

设有序变量依次为x1,x2,…,xn，其中每个变量代表公交客流小时刷卡数据，是一维向量。如果出最小误差函数e随分段数k变化的曲线，取该曲线拐弯处或开始变平处对应的分段数作为最适宜的分段数。

4）求解最优分段。确定分段数k后，在所有可能的分段方案表示对样本x1,x2,…,xn的最优k分割，则一定是在某一个截尾子段的最优k-1分割之后再添加一段形成的。这样就可以从各个截尾子段的最优二分段出发，建立一种递推公式求出各种k值下的最优分割，从而使得求最优分割的精确解得以实现。具体步骤如下：

1）定义类直径。设变量x1,x2,…,xn的某一归类为其均值向量

则类直径

2）定义误差函数。将n个样本划分为k个区间段，为记号简单，变量xi用下标i表示，用表示某一种分法，即

其中1=i1＜i2＜…＜ik≤n，定义这一分类的误差函数

当n和k给定时，总离差平方和一定，当类内平方和越小，则类间平方和越大，分类越合理。因此，聚类的目的是要找到一种分法使误差函数达到最小。

3）确定区间划分个数。有序聚类法本身并未给出合适的划分段数。本研究通过做中找出使达到极小值的最优k分段，记为若要将样本划成k段，首先确定jk使得达到极小值，即满足

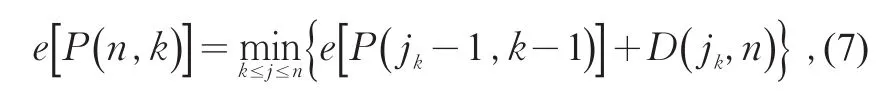
2 人工调查抽样方案

2.1 抽样率计算

调查成本及调查精度是抽样调查的主要关注点。因此，在保证一定精度的条件下减少费用或在限定费用的条件下尽量提高精度十分重要。若不考虑非抽样误差，调查精度与样本量在一定范围内直接正相关。当抽样样本超过一定数量后，单位样本量的增加对于精度的提高效果不再明显。同时，调查成本与样本量基本呈线性正相关关系。应该存在一个合适的抽样率，使得调查精度与调查成本达到均衡最优。这可以被归结为一个多目标最优化问题：抽样率f为决策变量，两个目标分别为调查成本最低及调查精度最高。

在公交客流跟车调查过程中，调查成本C调主要包括两个部分：固定成本C固和变动成本C变。前者指与样本量大小无关的成本，包括宣传费用、调查组织协调费用等；后者是随样本量增加而增加的成本。如果单位样本量的调查成本(包括人工费和材料费等)为C单，实际运营车辆数为N，抽样率为f，则调查成本

在统计学中，通常以允许相对误差r来表示要求的精度。由简单随机抽样的样本量计算公式

式中：n为样本量；n0为重复抽样样本量。可以计算得到样本的允许相对误差r相对于抽样率f的公式为

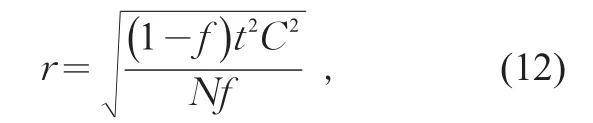
式中：t为对于一定置信度的百分位限值，当置信度为95%时t=1.96；s为总体标准差；为总体均值；C为总体变异系数，

由上可知，调查成本与调查精度两个指标衡量量纲不同，需要对两个指标进行量纲统一化处理。本研究从成本角度出发，提出调查精度成本折算系数Cr，将调查精度转换为成本进行分析。值得一提的是，在不同调查过程中实施者对成本和精度的关注度不同，借鉴多目标规划求解中加权求和的基本思想：决策者和分析者事先交换意见，根据p个目标的重要程度不同，分别乘以一组权系数然后相加作为目标函数，将多目标规划问题转换为单目标规划问题求解，即

研究中根据具体调查情况，对调查成本和调查精度折算成本赋予权重。根据实际情况对二者的重视程度和限制要求赋予权重，两权重之和为1。由此得到两个指标的总成本与抽样率的关系

式中：λ1，λ2分别为调查成本和调查精度折算成本的权重，且λ1+λ2=1。当r=1时，即调查允许相对误差为1，调查精度最差，则认为花费在此次调查中的变动成本全部无效；在调查线路的全部车辆时，成本最大，则Cr=NC单。那么，调查精度转化的成本rCr越小，得到的调查精度越高。因此，计算合适的调查率，使得调查成本与调查精度达到均衡最优，即求得C总的最小值。对公式(14)关于f求导，令导数为零，即可得到合适的抽样率取值。

2.2 抽样车辆确定

通常情况下，公交客流量在一天中的不同时段有高有低，持卡乘客比例也不尽一致(如通勤时段乘客使用IC卡比例较高)，但在所划分的客流时段内具有一定的稳定性。因此，在获得代表线路不同时段内的IC卡比例和客流特征后，可作为同类型中其他线路的参考值测算各条线路的公交客流量。车辆抽样应遵循以下原则：确保抽样车辆在一天内的班次尽可能多，并且运营班次覆盖每一类客流时段。被选中车辆的首班发车时间定为抽样调查开始时间。此外，为避免按照优化计算确定的抽样车辆总量较少而不能覆盖聚类后的时段，需适当增加抽样车辆数量。

车辆抽样方法包含四个步骤：

1）从调查成本和结果精度两个角度出发，根据抽样率计算公式，考虑实际情况赋予调查成本和调查精度相应的权重，计算得到调查的最佳抽样率，并结合具体线路的车辆数，得到代表线路抽样调查的样本量(车辆数)；

2）提前对公交线路的基本调度信息进行详细梳理，了解所选调查日期的调度计划安排，明确各运营车辆当天的运营班次总数及具体运营时间；

3）根据有序样本聚类算法，利用代表线路历史时期的IC卡数据，对该线路一天的客流时段进行聚类划分；

4）比较该线路各运营车辆具体班次运营时间与聚类得到的公交客流时段，遵循车辆抽样原则和计算所得抽样车辆总量对车辆进行抽样。

3 公交客流规模测算案例分析

3.1 数据来源

本文使用的IC卡数据均来自于上海市某辖区IC卡系统终端，日期为2011年10月1日—2012年9月30日以及2012年11月20日，研究时段为5:00—20:00。该区现有公共汽车运营企业两家，公共汽车场站管理公司一家，停车场四家，公共汽车运营线路56条(包括市通郊线路14条、跨区线路10条、区内线路32条)，运营车辆518辆，从业人员1 850余人，每车日均运营380 km，日均发送47班次。人工补充调查日期为2012年11月20日(星期二)，补充调查日期的选择充分考虑了代表线路的客流波动情况和天气变化情况[11]。

3.2 相似线路聚类分析

利用SPSS18.0软件对该区33条信息完整的公交线路进行聚类分析。设置最小聚类数为2，最大聚类数为4。聚类方法选择Ward法(离差平方和法)，转换值标准化选择按照个案Z得分，其余均选择默认值。最终选择将线路聚为三类：类型一发车间隔较小、线路相对拥挤；类型二属于长距离线路、发车间隔中等；类型三属于短距离、不拥挤线路，平均发车间隔较长(见表1)。此时每类线路特征较明显且分类结果更加符合实际情况。

综合考虑三种类型线路的属性特征，各选取一条典型线路作为研究对象，分别为XN专线、SF专线和NQ7路，并以XN专线为例说明计算过程。

3.3 相似小时聚类分析

在线路相似小时聚类分析时，考虑到后续分析涉及逐小时的公交客流特征，所用数据应为每天每小时的完整数据。由于公共汽车在5:00前及20:00后客流量较少，且不是本研究重点关注的时段，因此选择5:00—20:00作为研究时段。

以XN专线的IC卡刷卡记录为基础数据，由于人工补充调查日期是星期二，因此在剔除异样数据后，取XN专线2011年10月1日—2012年9月30日期间所有星期二客流数据进行平均，以小时为单位进行统计，得到15个样本数据(见图1)。

为简化计算，以每小时客流量占全天客流量的比值作为聚类属性，得到有序聚类样本：X={5.59,11.54,10.32,5.82,4.45,4.07,4.48,4.42,4.57,5.48,6.74,9.39,8.93,7.88,5.87}。采用Fisher算法，可以做出最小误差函数e随分段数k变化的曲线(见图2)。曲线开始变平处对应的分段数为6，因此，将15个数据样本分为6段较为适宜(见表2)。

表1 公交线路聚类结果Tab.1 Bus routes clustering

图1 XN专线星期二小时客流量均值Fig.1 Average hour-flow of XN special line on Tuesday

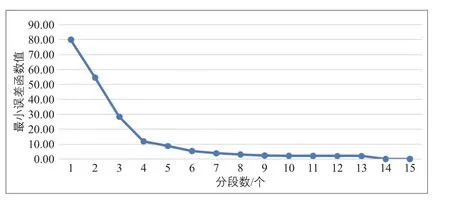
图2 分段数k与最小误差函数的关系Fig.2 Relationship between classification numberkand the minimum error function

表2 研究线路时段划分结果Tab.2 Time period classification of selected lines

3.4 抽样率计算

XN专线实际运营车辆17辆，调查选择95%的置信度，则t的取值为1.96。根据上海市历史数据计算得到总体变异系数C为0.26。从总体调查角度看，平均每条线路固定成本为500元，单辆车的调查成本为800元，则线路的调查精度折算成本为13 600元。本次调查没有明确强调成本、精度的重要性，故取λ1=λ2=0.5，据此可以得到线路不同抽样率下调查成本变化情况(见图3)。

在整个抽样调查中，调查精度与样本量在一定范围内直接正相关(图3中表现为调查精度折算成本与抽样率负相关)，然而，当样本量超过一定值后，单位样本量的增加对于精度的提高效果不再明显(在抽样率较高时，调查精度折算成本下降速度放缓)。

将线路数据代入公式(14)，对抽样率f求导，令导数为0，得到最佳抽样率为17%。因此，XN专线应抽样3辆车。采用类似方法，得到SF专线和NQ7路最佳抽样率分别为16%和22%，抽样量分别为3辆和2辆。

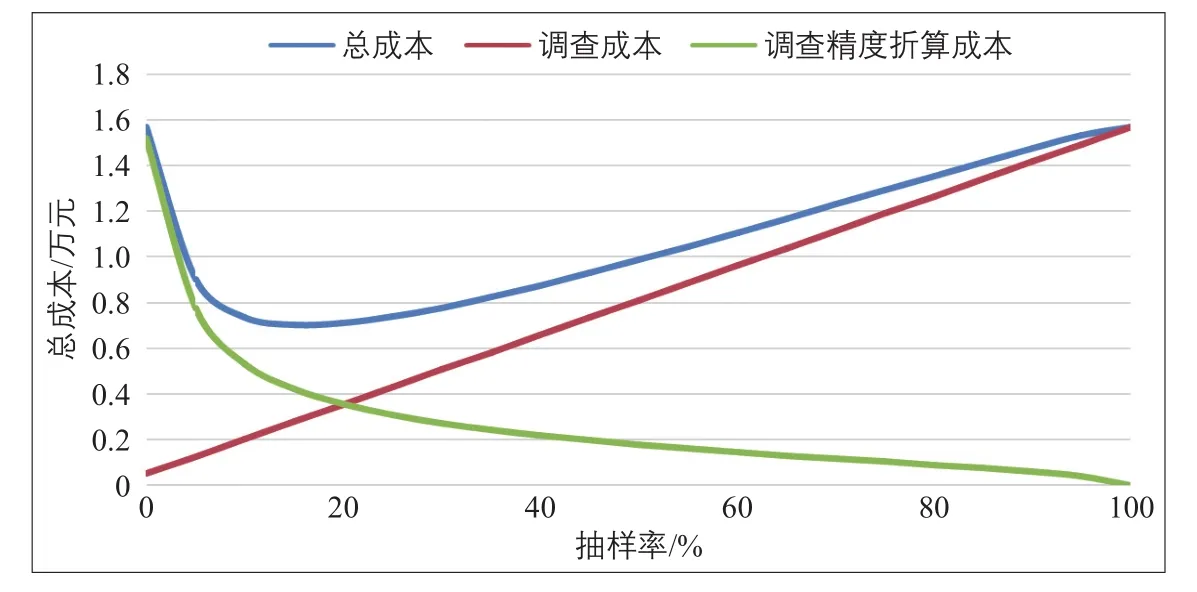
图3 XN专线调查成本曲线Fig.3 Curve of investigation cost of XN special line

3.5 抽样车辆确定

根据XN专线调度表可知，该线路首班车5:00从南桥汽车站发出，末班车22:35从莘庄地铁站发出，全日共74班次，包括XN专线上行方向36班次，下行方向38班次。为保证所选车辆运行时间在上、下行两个方向覆盖各个客流时段，最终选取3号、7号及12号车作为调查对象(见图4)。采用类似方法，得到SF专线调查开始时间依次为5:20，6:10及7:00；NQ7路调查开始时间依次为5:25和6:34。

3.6 日客流量测算

IC卡数据结构多样，首先应筛选分析所需的四个字段：线路代码、设备代码、交易发生日期及交易发生时刻。然后根据线路代码对照表筛选出调查线路，根据设备代码对照表筛选出调查车辆。如果没有设备代码对照表，可根据跟车调查记录的到站时间匹配相同时间的刷卡记录，在整条数据中即可查询对应的设备代码。将三组人工补充调查数据按时间进行加和汇总，将整合后的上客数及刷卡人数统计表格转化为以30 min为单位的统计表，根据客流时段划分结果将IC卡数据比例分别取平均值，得到各客流时段IC卡刷卡量占客流总量的比例(见表3)。

显然，IC卡比例在不同类型线路间以及各个时间段内均有很大差异。总体而言，类型三线路(以NQ7路为代表)的持卡比例整体较高，主要因为类型三线路基本均为区内线路，线路长度较短，乘客类型同质性较强。分时段对比，类型一线路(以XN专线为代表)在早晚高峰时段的持卡比例明显高于其他时段，主要因为类型一线路发车间隔较小，线路相对拥挤，属于典型的通勤线路；类型二线路(以SF专线为代表)属于跨区线路，距离长，发车间隔长，因此在9:00—16:00的非高峰时段持卡比例最高，与居民进出市中心的情况比较吻合。

图4 XN专线调查车辆运营时间对应的研究时段Fig.4 Time periods corresponding to operational time of surveyed vehicles of XN special line

使用MySQL软件中的SQL语句编写该线路客流总量的代码，将人工补充调查日期当天的IC卡数据导入程序内，经过扩样运算得到各线路的日均客流量(见表4)。

4 结语

本文基于调查成本与调查精度的综合考虑，在对不同线路IC卡流量特征的观测基础上，提出采用通过聚类分析获取补充调查的代表线路，并基于代表线路客流时段特征的差异，采用Fisher算法对代表线路的调查时段进行划分，从而对同一线路获取多个时段的IC卡数据扩样系数，并将之应用于同类型其他线路的IC卡客流扩样，从而获得公交日客流量。这对于城市公共交通规划和公交补贴政策的执行具有一定的参考价值，也在实际过程中得到很好的应用。此外，补充调查日期的选取非常关键，目前一般的方法是基于经验。本研究采用的补充调查日期严格考虑了客流波动情况和天气影响情况，尽量选择能够代表客流年日均值的时间进行调查[11]，这是进行公交客流规模测算时需要注意的方面。

表3 研究线路各时段IC卡比例Tab.3 IC card using rate of selected lines in each time period

表4 各线路类型客流总量统计结果Tab.4 Total volume for each type of bus lines人次·d-1

[1]陈学武，戴霄，陈茜.公交IC卡信息采集、分析与应用研究[J].土木工程学报，2004，37(2)：105-110.Chen Xuewu,Dai Xiao,Chen Qian.Approach on the Information Collection,Analysis and Application of Bus Intelligent Card[J].China Civil Engineering Journal,2004,37(2):105-110.

[2]陈绍辉，陈艳艳，赖见辉.基于GPS与IC卡数据的公交站点匹配方法[J].公路交通科技，2012，29(5)：102-108.Chen Shaohui,Chen Yanyan,Lai Jianhui.An Approach on Station ID and Trade Record Match Based on GPS and IC Card Data[J].Journal of Highway and Transportation Research and Development,2012,29(5):102-108.

[3]Barry J,Newhouser R,Rahbee A,et al.Origin and Destination Estimation in New York City with Automated Fare System Data[J].Transportation Research Record,2002,1817(02-1045):183-187.

[4]郭婕.公交IC卡通勤乘客OD确定方法研究[D].南京：东南大学，2006.Guo Jie.The Method of Determining the OD of Bus IC Commuter[D].Nanjing:Southeast University,2006.

[5]陈君.基于IC卡数据的城市公共交通需求分析理论与方法[D].上海：同济大学，2009.Chen Jun.Research on the Travel Demand AnalysisofUrban PublicTransportation Based on Smart Card Data[D].Shanghai:Tongji University,2009.

[6]Chu K A,Chapleau R.Enriching Archived Smart Card Transaction Data for Transit Demand Modeling[J].Transportation Research Record,2008,2063:63-72.

[7]Chu K A,Chapleau R,Trépanier M.Driver-as-sisted Bus Interview:Passive Transit Travel Survey with Smart Card Automatic Fare Collection System and Applications[J].Transportation Research Record,2009,45(2105):1-10.

[8]Trepanier M,Morency C,Blanchette C.Enhancing Household TravelSurveysUsing Smart Card Data[C]//Transportation Research Board.Transportation Research Board 88th Meeting Compendium of Papers DVD.Washington DC:Transportation Research Board,2009(09-1229):1-15.

[9]陈学武，戴霄，杨敏.先进的公交出行数据采集分析方法[C]//交通系统工程与智能交通运输系统及智慧城市研究组.2005年海峡两岸智能交通运输系统学术研讨会暨第二届同舟交通论坛.智能交通运输系统研究与实践.上海：同济大学，2005：595-603.

[10]戴霄.基于公交IC信息的公交数据分析方法研究[D].南京：东南大学，2006.Dai Xiao.Approach on the Information Analysis of Urban Public Traffic Base on the Data of Bus Intelligent Card[D].Nanjing:Southeast University,2006.

[11]王婧.公交客流调查与数据分析方法研究[D].上海：同济大学，2015.Wang Jing.Research on Methods of Bus Ridership Survey and Data Analysis[D].Shanghai:Tongji University,2015.

[12]姜平，石琴，陈无畏，张卫华.公交客流预测的神经网络模型[J].武汉理工大学学报(交通科学与工程版)，2009，33(3)：414-417.Jiang Ping,Shi Qin,Chen Wuwei,Zhang Weihua.ForecastofPassengerVolume Based on Neutral Network[J].Journal of Wuhan University of Technology(Transportation Science&Engineering),2009,33(3):414-417.

[13]方开泰.有序样品的一些聚类方法[J].应用数学学报，1982，5(1)：94-101.Fang Kaitai.Some Clustering Methods for the Order Sample[J].Acta Mathematicae Applicatae Sinica,1982,5(1):94-101.

[14]Fisher W D.On Grouping for Maximum Homogeneity[J].Journal of the American StatisticalAssociation,1958,53(284):789-798.

Passenger Volume Estimation Based on Data Fusion

Li Linbo1,Jiang Yu1,Wang Jing2,Wu Bing1
(1.The Key Laboratory of Road and Traffic Engineering of the Ministry of Education,Tongji University,Shanghai 201804,China;2.Ji'nan City Planning and Design Institute,Ji'nan Shandong 250101,China)

Accurate passenger flow estimation through surveys does not come without costs.This paper proposes a data fusion method based on the data from public transit IC card and supplementary surveys to accurately estimate passenger flow information.This paper first divides bus service routes into groups by their characteristics using cluster analysis method,and then selects one representative route from each group.Based on the temporary variation of bus passenger flow extracted from IC cards data,the paper categorizes IC card charging records per hour using Fisher algorithm of ordered sample cluster.By grouping time periods with similar IC card charging volumes,the paper determines the optimized sample rate and corresponding buses for the supplementary surveys.Consequently,bus passenger flows are estimated by data fusion method.Taking one district in Shanghai as an example,the paper demonstrates how to estimates daily passenger volumes of three types of bus routes using the above method.

public transit;passenger volume;cluster analysis;data fusion;public transit IC card;Shanghai

1672-5328（2016）01-0043-08

U491.1+7

A

10.13813/j.cn11-5141/u.2016.0107

2015-09-15

国家自然科学基金面上项目“基于出行服务链的城镇群交通模式发展研究”(51178346)

李林波(1974—)，男，湖南岳阳人，副教授，主要研究方向：交通规划与管理。

E-mail:llinbo@tongji.edu.cn