Fracture Characterization of High-Density Polyethylene Materials Using the Energetic Criterias
M.N.D.Cherief,M.Elmeguenni,M.Benguediab
1 Introduction
The use of polymer materials keeps increasing significantly in the recent decades,especially,the pressure pipe applications.As a consequence,this plastic material is requesting the use of a new methodology of analysis in order to assess the capability of this type of material to resist to different and complex loading.That’s why the study of the behavior of these materials arouses currently a great interest in the world of research.Many recent papers in fracture analysis of complex solid structures and materials are presented see[Dong and Atluri(2012,2013)].The fracture toughness of HDPE is lower than that of commercial metallic and ferrous alloys.In addition,its strength and rigidity are low compared to both metals and concrete,which is partially offset by its low weight(specific strength)[Tarek,ELBagory,Hossam,Sallam,Maher,and Younan(2014)].All the aspects of chain microstructure,e.g.,molecular weight and its distribution,monomers content and its distribution,long-chain branching and its distribution and short-chain branching and its distribution,are important characteristics that intensely affect the mechanical and rheological properties of polymers in particular.
Semi-crystalline polymers are heterogeneous and compressible at the solid state,therefore the impact of microstructure on mechanical properties is affected by disturbing parameters,i.e.,crazes and cracks,while in the molten state homopolymers are incompressible and homogeneous and the influence of microstructure on rheological properties is not affected by such distractions[Eskandari,Nekoomanesh,Ahmadi,and Arabi(2012)].
In the other hand,both types of loading,static[Chan and Williams(1983)]and dynamic[Hertzberg and Manson(1980)],are capable of initiating a brittle cracking,and causing propagation in a slow stable manner,either a critical crack size is attained for fast fracture,or until the net section stress is high enough for ductile failure[Sandilands and Bowman(1986)].The mechanical properties of polymeric materials are indeed sensitive to many parameters,even under normal operating conditions,such as loading rate and temperature[M.Bendouba,Djebli,Aid,Benseddiq,and Benguediab(2015)].
Besides,Impact behavior of semi-crystalline polymers has received considerable attention in recent years,and has been investigated by many authors.According to Plati and Williams(1975);Vu-Khanh and Charentenay(1985);Vu-Khanh and Fisa(1990);Vu-Khanh(1994)polymers can break in very distinct manners under impact.The fracture tests on the samples with different crystalline morphologies revealed that,depending on the composition,unstable(Brittle)and stable(Ductile)fracture could occur[Elmajdoubi andVu-Khanh(2003)].Several modes of fracture have been identified depending on the amount of plastic deformation at the crack tip and the stability of crack propagation.For each mode,an appropriate analysis must be used to determine the impact fracture energy of the material[Mamat,Vu-Khanh,Cigana,and FAVIS(1997)].
Actually,the aim of this paper is to investigate some analytical approaches,analyze and/or propose modification or a new approach based on the two criteria used for the impact fracture concept of Plati and Williams(1975);Mamat,Vu-Khanh,Cigana,and FAVIS(1997).
2 Material and experimental methods
In this subsection,the investigated material is described,the specimen’s geometry and the experimental procedure are presented.The polymer investigated in this work,is the High-density polyethylene(HDPE).It’s one of the most used polymers in the world,for his large variety of industrial applications,in particular for packaging industries;of Building and Public Works.The HDPE is a thermoplastic polymer with good strength,toughness and resistance to acids as well as aging.
2.1 Material characteristics
The HDPE materials was provided by a piping company.The physical properties are:density 0.9(g/cm3),Melt-Mass-Flow=1.2(g/10 min),Molecular-Weight 310000,Glass Transition Temperature=84(°C)and the Melting Point=180(°C),and crystallinity index ≈ 66%.The true strain at break is around 250%.The Young’s modulusEobtained from the initial slope is equal to 850 MPa.The yield stress σy,defined as the intersection point between the tangent at the origin and the tangent of the plateau before hardening,is equal to 25 MPa.
All specimens were machined from pipe samples supplied by an industrial company for piping.
In order to examine the sensitivity of the different approaches of the fracture mechanics concepts and examine their relevance regarding the highly deformable materials such as HDPE pipe materials,SENB specimen configuration(under Three Point Bending and Charpy test)was considered for the fracture toughness investigation.
2.2 Sample geometry
The specimen geometry is presented in Figure 1.Its depth was chosen according to ASTM E399(1997).Various crack lengths‘a’were studied.The normalized crack lengthsa/Wwere in the range of 0.35<a/W<0.6.
For the Three Point Bending,the fracture tests were conducted at room temperature under a constant displacement rateW/10 mm/min according to the specimen width as a basic test condition.
Impact fracture tests are made with Instrumented standard Charpy test.The standard test methods for Notched Bar Impact Testing of Materials are specified and used.

Figure 1:Schematic representation of SENB specimen configuration.
2.3 Methods and analysis
2.3.1 Static case
The three point bending tests have been conducted at a velocity ratioW/10 in order to highlight the first characteristic elements of the failure mode of HDPE,and verify the feasibility of the test method used to characterize the toughness.We begin by presenting the evolution of the load-displacement curves obtained from tests carried on specimens SEMB for different crack lengths(a/W).
2.3.2 Dynamic case
Charpy test served to determine the impact resistance of the HDPE material.Spite of his high ductility,HDPE is obviously sensitive to notch effects and likely to be brittle to large strain rate.Impact tests were carried out on a pendulum for assessing the energy absorbed during the fracture process.For these tests,a hammer of 5 Joules was selected.The total energy measured must remain between 10%and 60%of the maximum capacity of this hammer.The tests were made on a Ceast pendulum 9050(Impactor II)having a speed of impact 4 m/s approximately.
The fracture tests on the samples with different crystalline morphologies revealed that,depending on the composition,unstable(Brittle)or stable(Ductile)fracture may occur[Elmajdoubi and Vu-Khanh(2003)].
Brittle fracture occurs when the strain energy stored in the sample up to the point of fracture is much larger than the energy dissipated in the creation of the two fracture surfaces.In this case,the crack grows in an unstable manner.
The remaining part is transformed into kinetic energy.The sample generally tends to break completely into two halves and fly away after fracture,and for many poly-mers,with the naked eye,the surface appears rough and often shows a branching effect[Mamat,Vu-Khanh,Cigana,and FAVIS(1997)].
For this type of fracture mechanics,Williamset al.have proposed a model based on linear elastic fracture mechanics(LEFM)to determine the impact fracture energy.The energy absorbed by the specimen to break(U),can be related to the toughness of the material(GC).
The expression for the critical strain energy release rate or fracture energy is given by:

WhereBis the sample thickness,Wis its width,and φ is a geometrical function which can be evaluated for any geometry by considering the appropriate calibration factor established for pre-cracked samples.
For the ductile fracture behavior,another approach taking into account the crack initiation and crack propagation energies in the material has been proposed by[Vu-Khanh(1994)],assuming that the fracture energy of the polymer with ductile behavior varies linearly with crack extension and is given by:

In whichGris the actual fracture energy,Giis the fracture energy at crack initiation,Tarepresents the rate of change ofGrwith crack extension,andAis the fracture surface.
3 Results and discussion
The load-displacement curves for SENB specimen configuration with various crack lengths(a/W)were obtained.As expected,the increasement of initial crack length leads to a decrease of the maximum load.The curves were corrected by eliminating compression and pin penetration effects.One of the corrected curves is shown in Figure 2.
In general,the obtained results exhibits three levels behavior:an initial linear behavior followed by a nonlinear plastic behavior and an eventually a plastic softening.
The toughness is usually measured from the evaluation of the deformation rate energy per unit thickness for a displacement or critical load,the energy absorbed during the fracture of the material is obtained by integrating the area under the curve Figure 2.

Figure 2:Load-plastic displacement curve.

Figure 3:Plastic energy versus the normalized crack length.
Figure 3 shows the variation of the energy by thickness unitU/Bversus the crack length.It is clearly observed that at constant displacement,the evolution of the energy can be estimated linear in the first approximation.
In order to characterize,understand better the fracture behavior concept,and to identify the microstructural processes of damage of the HDPE,the area near the crack-tip was observed by means of a field emission scanning electron microscope(FESEM Hitachi-S4700)using secondary electrons.In Figure 4,the fracture surface of SENB specimen is shown.

Figure 4:Micrograph around the crack tip and details for four magnifications.
It exist three possible modes of crack propagation:stable propagation which translates a ductile behavior,unstable propagation for a brittle behavior and a mixed propagation in the case of a combination of the previous modes.The energy of propagation depends on the mode of propagation which itself depends on the length of the initial notch and can go from “totally unstable”to “mixed”and then “completely stable”when increasing this length Figure 5.
In general,after impact,the load increases at a rate corresponding to the notched compliance of the specimen.The phase(1)include the formation of a craze zone at the notch tip which is later seen on the fracture surface of the material.
After the initial phase,there is a rapid crack propagation,which corresponds to the development of a smooth zone in the center of the specimen(2).
Finally,the last region is related to the extension of the shear lips and the rotation of a ductile hinge on the fracture surface of the material(3).
Figure 6 presents the total energy absorbed as a function ofBWφ for unstable fracture(Brittle),in the other hand,Figure 7 shows the variation of the total energy absorbed versusB(W−a)for a stable fracture(Ductile).Given the nature of the propagation,the propagation energy is the slope of the lines obtained.
It’s very difficult to measure the exact load deflection curve and to evaluate the exact fracture toughness under the dynamic loading condition,so we are obliged to use the energetic criteria in this paper.Now we will present an analytical study in order to propose a new mixed approach of the two modes of fracture(brittle and ductile)with a change in the energy equation based on Williams and Vu-Khanh approaches.

Figure 5:Fracture Surface of an impacted sample.
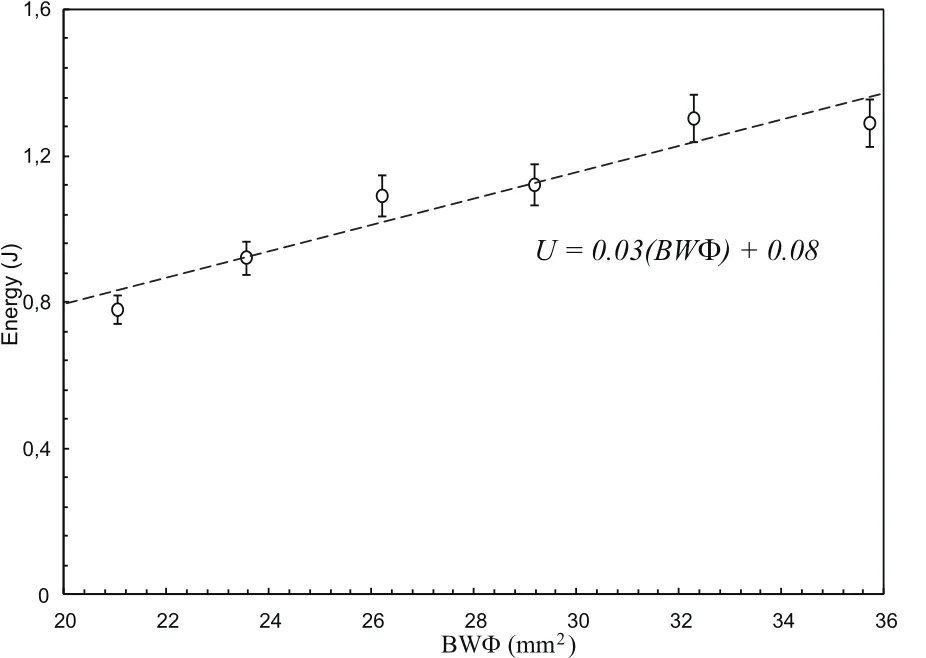
Figure 6:Energy values evolution for unstable fracture(Brittle).

Figure 7:Energy values evolution for a stable fracture(Ductile).
From Figure 6 we have:

From Figure 7 we have:

Williamset alhave shown that:

In the case of the Three Point Bending,we have:

With:

For the other constant:
With

Eq.6 becomes

The tests are made with distance between supports given as:S=4WSo:

The corresponding(Y)function given by Brown and Srawley(1966)is:

Combining and replacing all the values in Eq.12,the geometry factor(φ)can be determined for all(a/W)conditions used in this study Figure 8.

Figure 8:Geometry factor(φ)values determined for arc-shaped specimens.
So,after analysis we obtained the following results:

We replace Eq.14 in Eq.4 to write the equation of the total energy as a function of a single parameter(a/W),so Eq.4 becomes:

After factorization,Eq.5 becomes:

Then the equation of the total energy will be written:


The length of notch should respect the condition:

Figure 9:Energy values evolution for dynamic testing.
HDPE specimens were tested for determining impact energy per unit area(BW)according to notch depth ratios(a/W)for static and dynamic load which are analyzed and compared.
The figures show the evolution of the energy byBWΦ for unstable fracture(figure 6),and the energy evolution as a function ofB(W−a)for stable fracture(figure 7).As we can see,in the both cases;unstable and stable fracture there is an increase of energy.

Figure 10:Static testing vs dynamic testing.
In this analytical study,an equation(figure 9)based on vu-khann and Williams approaches has been determined to describe the two modes of fracture(brittle and ductile)and to compare the total absorbed energy as a function of one parameter(a/W)for both cases,static(Three Points Bending)and dynamic loading(Charpy)(figure 10).
The results of this study show that there is a significant difference between static and dynamic testing.The absorbed energy per unit area of each types of loading(static and dynamic)decreased when the notch depth ratio of HDPE increased.According to Mehmet,Necmettin,Avcı,and Erkendirci(2014)]the predominant type of damage that occurred in the Charpy impact test originates from delamination damage of HDPE.However,the reason in decrease of absorbed energy are fast crack propagation.The absorbed energy per unit area for dynamic load are higher than static load in all notch depths,It was shown that there is a velocity influence due to the nonlinearity of the contact stiffness between Charpy specimen’s and striker[Rager,Williams,and Ivankovic(2003)].According to Martínez,Arencón,Rodríguez,and Salazar(2014);Major and Lang(2002)the high rate fracture testing has special problems because of the presence of dynamic effects:vibrations in the test system and inertial loads create forces on the specimen different from the forces in the hammer.Decreasing the testing rate reduces dynamic effects,and some control of the effect of inertial loads may be achieved by mechanical damping of the load transmission.
4 Conclusion
In this paper,the mechanical behavior in large plastic deformation of a HDPE material was studied by using experimental and analytical methods.
The material was tested experimentally under static and dynamic tests with SENB specimen by using the Three Point Bending and Charpy impact tests(brittle and ductile for a stable and unstable propagation).
In addition,the fracture toughness of this material was analyzed in an analytical study based on two different approaches in order to propose a new mixed approach for the two modes of fracture.The main findings are given below.
·The absorbed energy per unit area of each types of loading(static and dynamic)decreased when the notch depth ratio of HDPE increased.
·The predominant type of damage that occurred in the Charpy impact test originates from delamination damage for HDPE.
·The absorbed energy per unit area for dynamic load are higher than static load in all notch depth.
·The reason of decrease in absorbed energy are fast crack propagation.
The main objective was to check the validity of the used concepts,and to show difference between the static and dynamic fracture mechanics and to determine correct impact fracture resistance values for the designated specimens and to fill a gap in this area of research.
Bendouba,M.;Djebli,A.;Aid,A.;Benseddiq,N.;Benguediab,M.(2015):Time-dependent J-integral solution for semi-elliptical surface crack in HDPE.CMC:Computers,Materials&Continua,vol.45,no.3,pp.163–186.
Brown,J.W.F.;Srawley,J.E.(1966):In plane strain crack toughness testing of high strength metallic materials.ASTM STP 410,American Society for Testing and Materials,pp.1–65.
Chan,M.K.V.;Williams,J.G.(1983):Slow stable crack growth in high density polyethylenes.Polymer,vol.24,pp.234–244.
Dong,L.;Atluri,S.N.(2012):SGBEM(UsingNon-hyper-singularTractionBIE),and super elements,for non-collinear fatigue-growth analyses of cracks in stiffened panels with composite-patch repairs.CMES:Computer Modeling in Engineering&Sciences,vol.89,no.5,pp.417–458.
Dong,L.;Atluri,S.N.(2012):SGBEM Voronoi Cells(SVCs),with embedded arbitrary shaped inclusions,voids,and/or cracks,for micromechanical modeling of heterogeneous materials.CMC:Computers,Materials&Continua,vol.33,no.2,pp.111–154.
Dong,L.;Atluri,S.N.(2013):Fracture&fatigue analyses:SGBEM–FEM or XFEM.Part 1:2D structures.CMES:Computer Modeling in Engineering&Sciences,vol.90,no.2,pp.91–146.
Dong,L.;Atluri,S.N.(2013):Fracture&fatigue analyses:SGBEM–FEM or XFEM.Part 2:3D solids.CMES:Computer Modeling in Engineering&Sciences,vol.90,no 5,pp.379–413.
Elmajdoubi,M.;Vu-Khanh,T.(2003):Effect of cooling rate on fracture behavior of polypropylene.Theoretical and Applied Fracture Mechanics,vol.39,pp.117–126.
Eskandari,J.J.;Nekoomanesh,M.;Ahmadi,M.;Arabi,H.(2012):From molecular weight distribution to linear viscoelastic properties and back again:application to some commercial high-density polyethylenes.Iran Polym J,vol.21,pp.403–413.
Hertzberg,R.W.;Manson.(1980):Fatigue of Engineering Plastics.Academic Press,London.
Major,Z.;Lang,R.W.(2002):Determination of rate dependent fracture toughness of plastics using precracked charpy specimens.European Structural Integrity Society,vol.30,pp.137–144.
Mamat,A.;Vu-Khanh,T.;Cigana,P.;FAVIS,B.D.(1997):Impact Fracture Behavior of Nylon-6/ABS Blends.Journal of Polymer Science Part B:Polymer Physics,vol.35,pp.2583–2592.
Martínez,A.B.;Arencón,D.;Rodríguez,J.;Salazar,A.(2014):Influence of the notch sharpening on the impact fracture toughness of ethylene-propylene block copolymers.Polymer Testing,vol.36,pp.75–81.
Mehmet,T.D.;Necmettin,T.;Avcı,A.;Erkendirci,O.F.(2014):Fracture toughness of filament wound BFR and GFR arc shaped specimens with Charpy impact test method.Composites Part B:Engineering,vol.66,pp.7–14.
Plati,E.;Williams,J.G.(1975):The determination of the fracture parameters for polymers in impact.Polymer Engineering and Science,vol.15,pp.470.
Rager,A.;Williams,J.G.;Ivankovic,A.(2003):Numerical determination of the energy calibration function gd for high rate charpy impact tests.European Structural Integrity Society,vol.32,pp.199–205.
Sandilands,G.J.;Bowman,J.(1986):An examination of the role of flaw size and material toughness in the brittle fracture of polyethylene pipes.Journal of materials science,vol.21,pp.2881–2888.
Tarek,M.A.A.E.-B.;Hossam,E.M.S.;Maher,Y.A.Y.(2014):Effect of strain rate,thickness,welding on the J-R curve for polyethylene pipe materials.Theoretical and Applied Fracture Mechanics,vol.74,pp.164–180.
Vu-Khanh,T.(1994):Impact fracture characterization of polymer with ductile behavior.Theoretical and Applied Fracture Mechanics,vol.21,pp.83–90.
Vu-Khanh,T.;Charentenay,F.X.(1985):Mechanics and mechanisms of impact fracture in semi-ductile polymers.Polymer Engineering and Science,vol.25,pp.841–850.
Vu-Khanh,T.;Fisa,B.(1990):Effects of fillers on fracture performance of thermoplastics:Strain energy density criterion.Theoretical and Applied Fracture Mechanics,vol.13,pp.11–19.
 Computers Materials&Continua2016年3期
Computers Materials&Continua2016年3期
- Computers Materials&Continua的其它文章
- A Numerical Study Comparing The Effect on Residual Stresses of Two Different Types of Projectiles During Shot Peening
- A Model to Describe the Fracture of Porous Polygranular Graphite Subject to Neutron Damage and Radiolytic Oxidation
- Higher-Order Line Element Analysis of Potential Field with Slender Heterogeneities
