“对应”十法

江西 曾建生

“对应”十法

江西 曾建生

分数应用题有一个共同的特点，就是每一个具体数量总对应着一个分率，每一个分率也有一个具体数量和它对应。然而，有些题目数量关系比较复杂，具体数量与分率没有直接对应。这时，正确找出量率对应的关系就成为解答这类题目的关键。找对应的方法很多，下面介绍十种方法，供同学们参考。

一、画图找对应

【分析与解】根据题意可画出如下线段图：

二、列表找对应

【例2】第一个鱼缸里有8条金鱼，第二个鱼缸里有6条金鱼，现在向两

个鱼缸里共放进16条金鱼后，第二个鱼缸里的金鱼数正好是第一个鱼缸的。每个鱼缸各放进多少条金鱼？

【分析与解】根据已知条件“第二个鱼缸里的金鱼数正好是第一个鱼缸的”，我们可以把第一个鱼缸现有的金鱼数看作单位“1”，再设法找到能确定的金鱼条数和相对应的分率。列表如下：

三、假设找对应

【例3】甲、乙两个粮库共存粮264吨，如果从甲粮库中调出，乙粮库中调出，则共调出78吨粮。甲、乙两个粮库原来各存粮多少吨？

四、整体找对应

【例4】某果农把一批苹果装筐送往水果批发市场。第一次搬出这批苹果的，共装29筐还剩5千克；第二次搬出剩下的苹果和第一次装筐

剩下的5千克共装21筐。这批苹果共有多少千克？【分析与解】根据题意画出示意图：

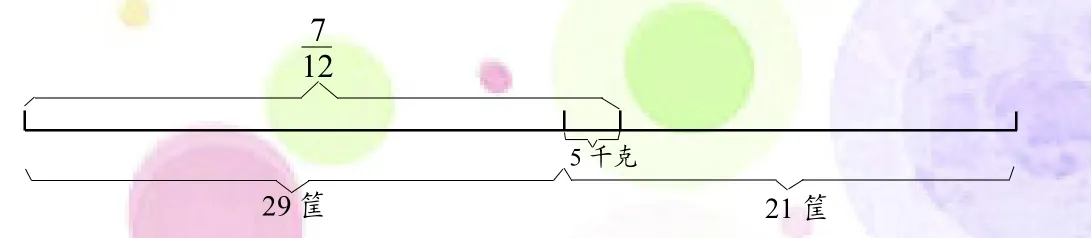
因为从搬出的份数这个角度找不到和5千克对应的分率，因此要从装筐的角度进行整体分析。29筐占总筐数的，即29筐苹果占这批苹果的，所以，5千克对应的分率是，那么这批苹果有5ч=1500(千克)。

五、倒推找对应

六、重叠找对应

【分析与解】分析题意可知，(54+90)表示的是第一层、第二层、第三层和第四层共有的本数，其中第二层出现了两次，也就是(54+90)表示的是这个书架上书的总数加上第二层书的本数。又知道第二层书占这个书架书的

【例6】一个书架有四层，第一层和第二层共有54本书，第二、第三和第，由此可求出余下油的重量是20ч

=30（千克）。根据“第一次用去全桶的

七、比较找对应

【分析与解】列式对应比较分析：

八、按份数找对应

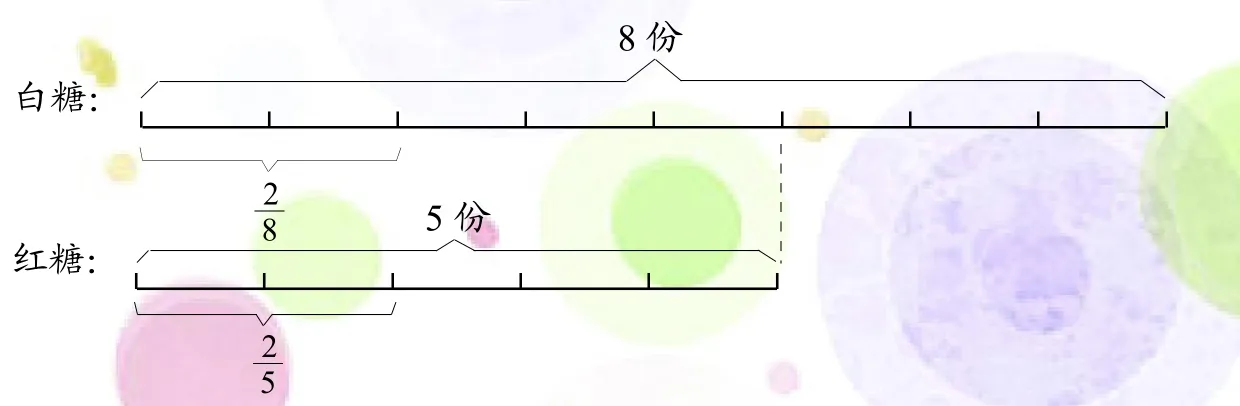
由图可知，白糖和红糖的相应份数分别是8份和5份，再根据“白糖重量的与红糖共重620千克”，可以求出620千克的对应分率，即8Ч+5=，所以白糖的重量是620чЧ8=480(千克)。

九、移多补少找对应

【例9】甲、乙两人合作加工一批零件，完工时，甲加工了全部零件的少20个，乙加工了全部零件的多30个。这批零件有多少个？

【分析与解】题目中既有少20个，又有多30个，可以采用移多补少法。将乙加工零件数中的20个给甲，那么题目的条件就转化成：甲加工了全部零件的，乙加工了全部零件的多10个。所以10对应的分率就是(1)，这批零件有(3020)ч()=300(个)。

十、将比转化成分率找对应

【例10】张师傅加工一批零件，第一天完成的个数与未完成的个数之比是1∶2。如果再加工15个就可以完成这批零件的一半。这批零件共有多少个？

【分析与解】本题的关键是要找出15个对应的分率，那就需要先把比转化成分率，再找出隐含的分率。“第一天完成的个数与未完成个数的比是1∶2”，这句话可以理解为：第一天完成的个数是零件总个数的，这批零件的一半就是这批零件的。那么，15个对应的分率就是()

【练一练】

4.计划将一批零件按9∶7分给师徒加工，实际完成加工任务时，师傅加工了零件总数的，比分配给他的计划多加工30个零件。师傅计划加工多少个？

5.某地有甲、乙两个消防队，共有336人，抽调甲队人数的、乙队人数的，共抽调188人。甲、乙两消防队原来各有多少人？

参考答案

《小学数学五年级上册期末自测题》参考答案：

一、1.三十2.13.780.13780.532.63.＜＞=4.51.95195152.05.(5，2)(5，3) 6.4蓝黄7.a-3b46.5118.59.2410.280

二、1.Ч2.Ч3.Ч4.√5.Ч

三、1.C2.C3.C4.A5.B略

四、1.0.90.90.09；0.839.880.39；6.800.722.16.94.673.19.3512.89730

3.153.154.x=0.05x=0.5x=5

五、1.红色最多，黄色最少图略2.(1)略(2)平行四边形15cm2

六、1.4.5m2.1套3.363米4.第一根1.2m第二根3.6m5.1200kg6.18+3.1Ч12+4.7Ч3=69.3(元)