多孔钢波纹板拱桥地震时程响应分析

张百永

(安徽省交通规划设计研究总院股份有限公司，合肥 230088)



多孔钢波纹板拱桥地震时程响应分析

张百永

(安徽省交通规划设计研究总院股份有限公司，合肥 230088)

以泗许高速公路钢波纹板拱桥为例，利用有限元软件midas FEA建立了该桥的实际波纹形状有限元实体模型，根据现有的抗震分析理论，采用动态时程分析方法，考虑顺桥向、横桥向、三向叠加三种方向地震波，分析了该桥的地震响应性能。结果表明：研究同一个拱的拱脚处地震响应(位移、应力)最大，对于不同的拱跨，靠近两侧桥台处边跨更容易发生破坏；在三种方向地震波作用下，顺桥向和竖桥向位移较为明显，设计中应给予重点考虑。

钢波纹板；拱桥；实际波纹；时程分析

0 引 言

钢波纹板拱桥是一种新型结构形式，具有施工便捷、造型优美、价格低廉、环保等诸多优异性能，有着极强的生命力和广阔的应用前景。[1-2]在国外，已经有了比较成熟和完善的设计规范体系。[3]

目前，国内许多专家学者对其进行了较深入的研究。文献[4] 通过对钢波纹板涵洞进行野外现场测试，从不同的角度研究了其力学特征。文献[5]运用有限元的方法计算了不同回填高度下的拱圈弯矩和轴力，分析了回填高度对拱圈应力和变形的影响；文献[6]利用大型通用有限元软件ANSYS，通过等效钢波纹板的波纹形状，建立三维空间有限元实体模型，采用动态时程分析方法，对该桥在人工合成地震波、El Centro波及Taft波三种地震作用下分析位移和应力的规律。

从研究现状看，目前国内针对钢波纹板桥的研究主要集中在土压力方面[7]，而对于地震荷载的研究较少，因此非常有必要建立实际波纹形状的钢波纹板桥有限元数值模型用以研究地震荷载对于多孔钢波纹板桥的影响。

本文依托泗许高速公路一处三孔4 m钢波纹板拱桥，利用通用有限元软件midas FEA建立了该桥的实际波纹形状的三维空间有限元模型，利用动态时程分析法分析该桥在地震荷载作用下的力学性能。

1 工程概况

泗许高速公路钢波纹板拱桥图1，为3孔跨径4 m波纹钢拱结构形式。每孔跨度各4m、孔间墩身厚0.5m，桥长15.1m，路基宽12m，圆弧拱半径R为2.164 8m，中心角为135°，钢波纹板为150mm×50mm×28mm波形，厚度5mm，管顶覆土厚度1.2m、路面结构为18cm沥青混凝土面层加36cm水泥稳定碎石基层。墩台身为现浇钢筋混凝土结构。钢波纹拱和墩帽、台帽采用螺栓连接。

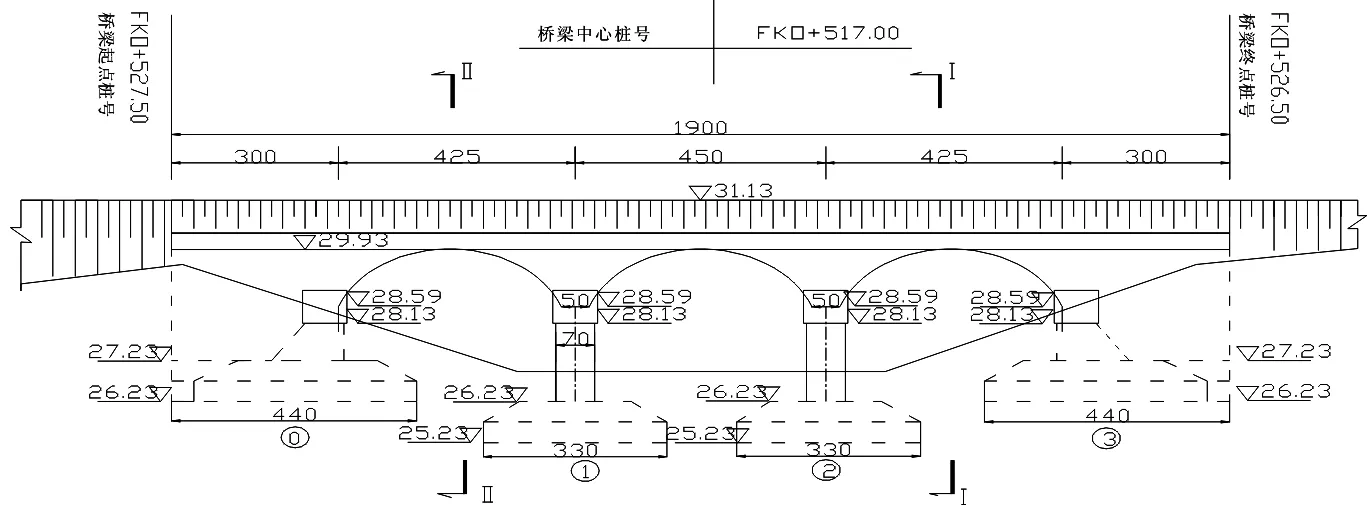
图1 钢波纹板拱桥立面布置图

2 有限元模型的建立

应用midas FEA有限元程序建立了钢波纹板拱桥结构三维空间模型如图2，模型尺寸为顺桥X方向桥长20.1m，横桥Z方向桥宽7.5m，竖直Y方向取2.6m。

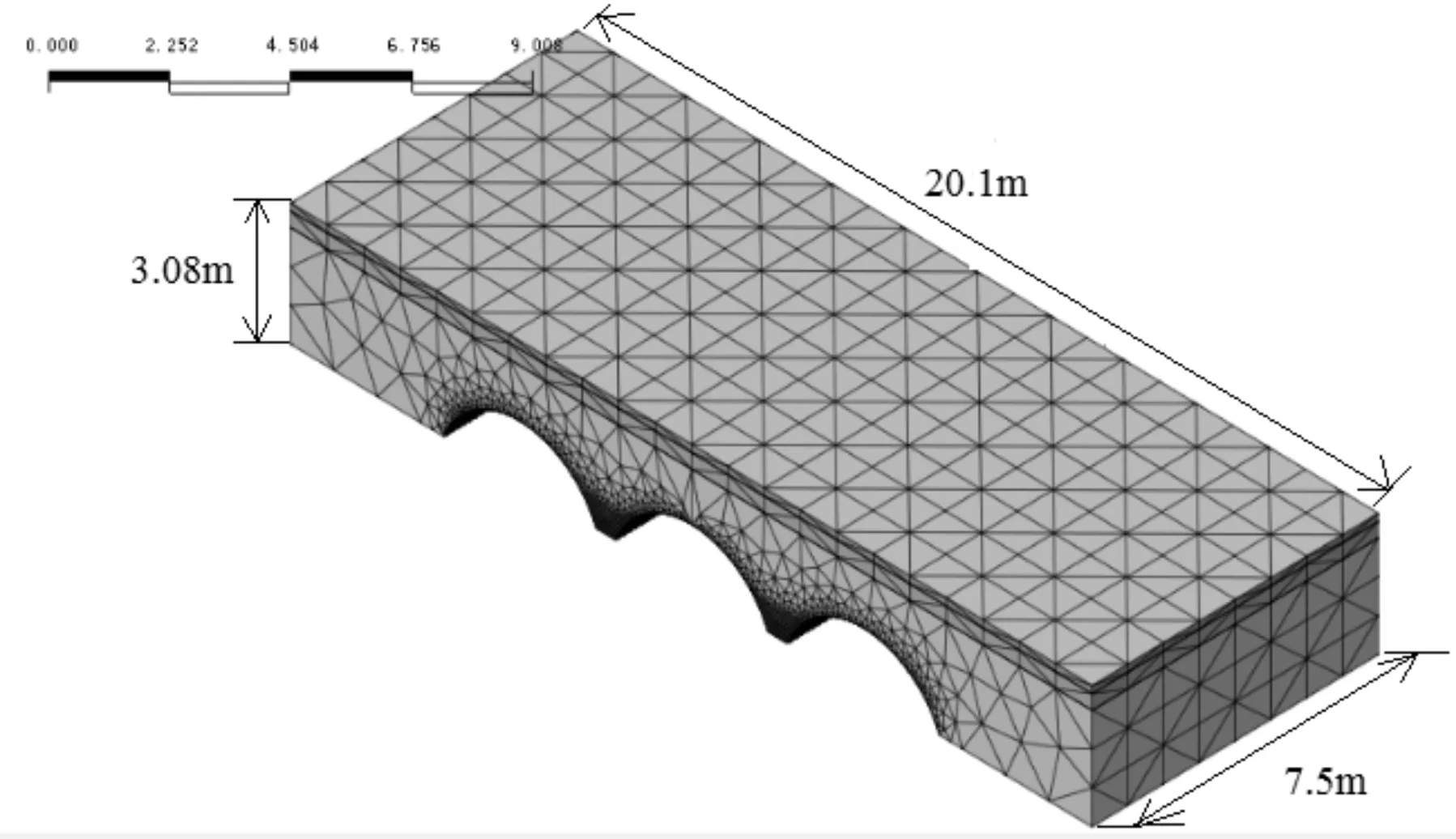
(a)钢波纹板拱桥整体模型图

(b)钢波纹板单元划分图

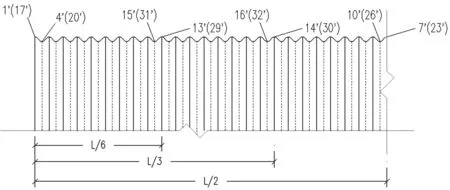
(c)拱顶控制点位置示意图

具体建模过程如下：(1)将具有一定波形的实际波纹钢板根据实际波形建立有限元模型，采用循环网格法，用三角形板单元模拟钢波纹板的受力情况。(2)根据彭贤明成果[8]，在结构受外荷载作用下，结构两侧一倍跨径内的土体变形较明显，一倍跨径以外的土体几乎无变化。考虑到这些方面本文取单倍跨径，采用循环网格法，用四面体实体单元模拟。(3)边界条件。本文对桥墩台进行建模时边界条件的具体说明如下：桥台底面以及墩底面由于受到地基作用，则在结构底部施加固定端约束；小桩号桥台台背侧立面由于受到覆土结构的作用，故在其上施加顺桥向水平约束，同理，大桩号桥台的台背侧立面也施加顺桥向水平约束；桥台的侧面由于受到覆土结构的作用，故对其施加横桥向水平约束。划分后单元总数275 408个，节点总数70 134个(见表1)。

表1 钢波纹板控制点说明

3 有限元模型的计算结果与分析

本文根据文献[9]现场实测的双车并行荷载工况下，中跨和边跨拱顶的应力随着荷载加载位置的实测值，与同种工况条件下的有限元模型模拟值进行对比分析如图3—4，分析结果可以得出如下结论：随着荷载移动，两者的应力变化情况是基本上是统一的，规律相同。在双车并行的条件下，中跨波峰位置两者相差最大绝对值不大于44.4%，波谷位置不大于42.2%，边跨波峰位置不大于29.2%，波谷位置不大于38.9%。且有限元模拟所得计算值在荷载同样的施加位置相对于实测所得数据较大些，说明本文通过采用有限元软件midas FEA，模拟钢波纹板实际波纹形状，建立有限元数值模型，对该多孔钢波纹板桥进行有限元分析是满足要求的，而且得出的结论和现场试验得出的规律是保持一致的，由此可以得出，本文的模型精度满足要求。

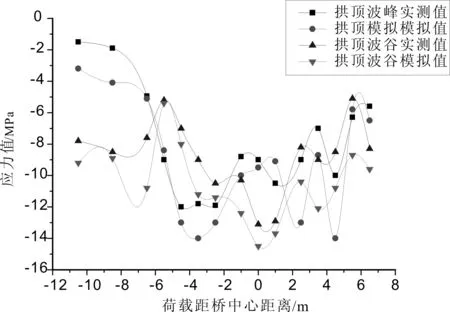
图3 双车并行条件下中跨应力值图

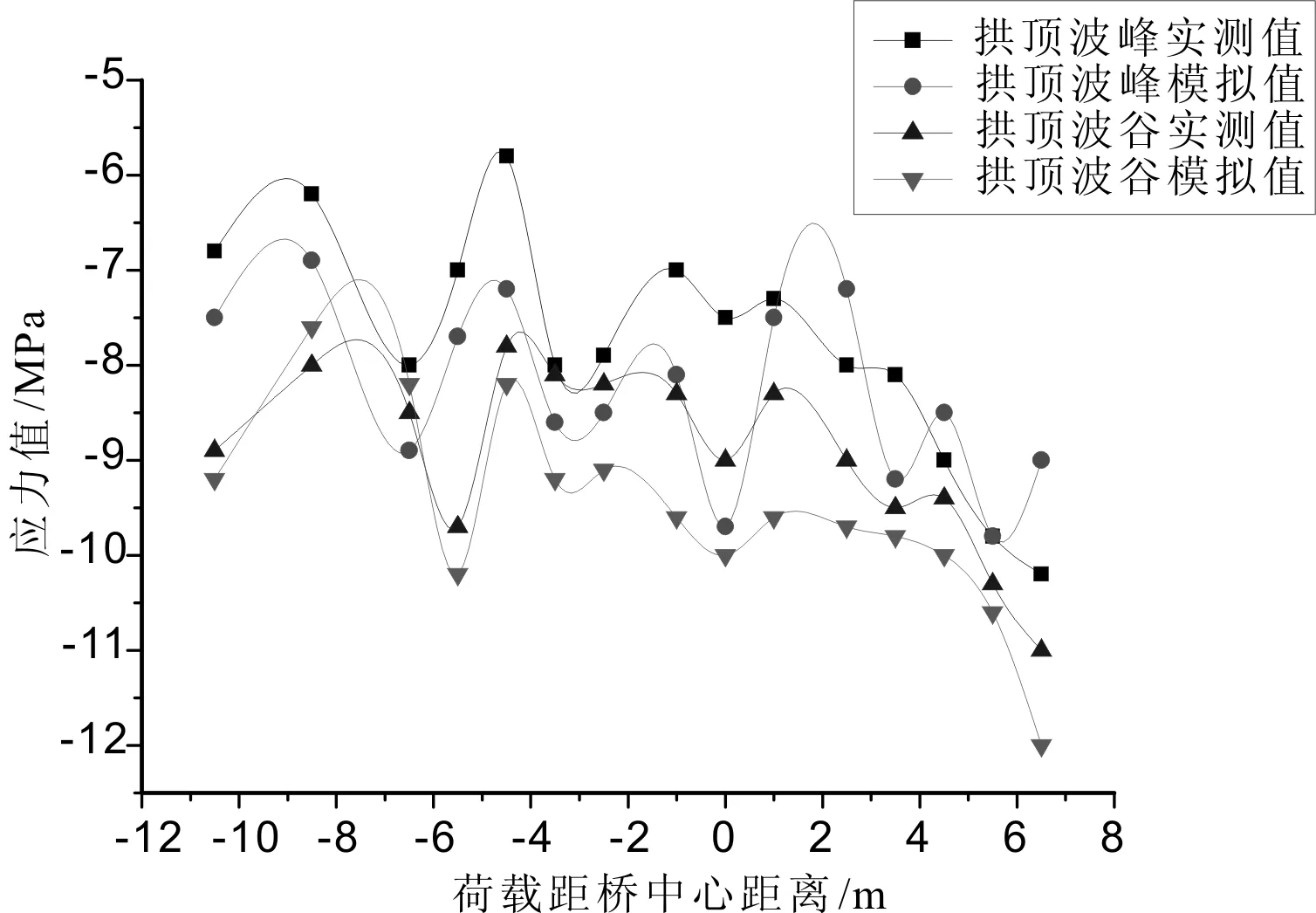
图4 双车并行条件下边跨应力值图

4 钢波纹板拱桥的自振特性

本文采用子空间迭代法，得到该结构的自振特性。通过计算，模型一阶自振频率为12.258Hz，主振型为反对称，双波浪型上翘或下弯；二阶自振频率为12.683Hz，主振型为正对称，双波浪型上翘或下弯，可以看出该种结构的刚度较大，如表2，为前十阶自振频率及振型计算结果。

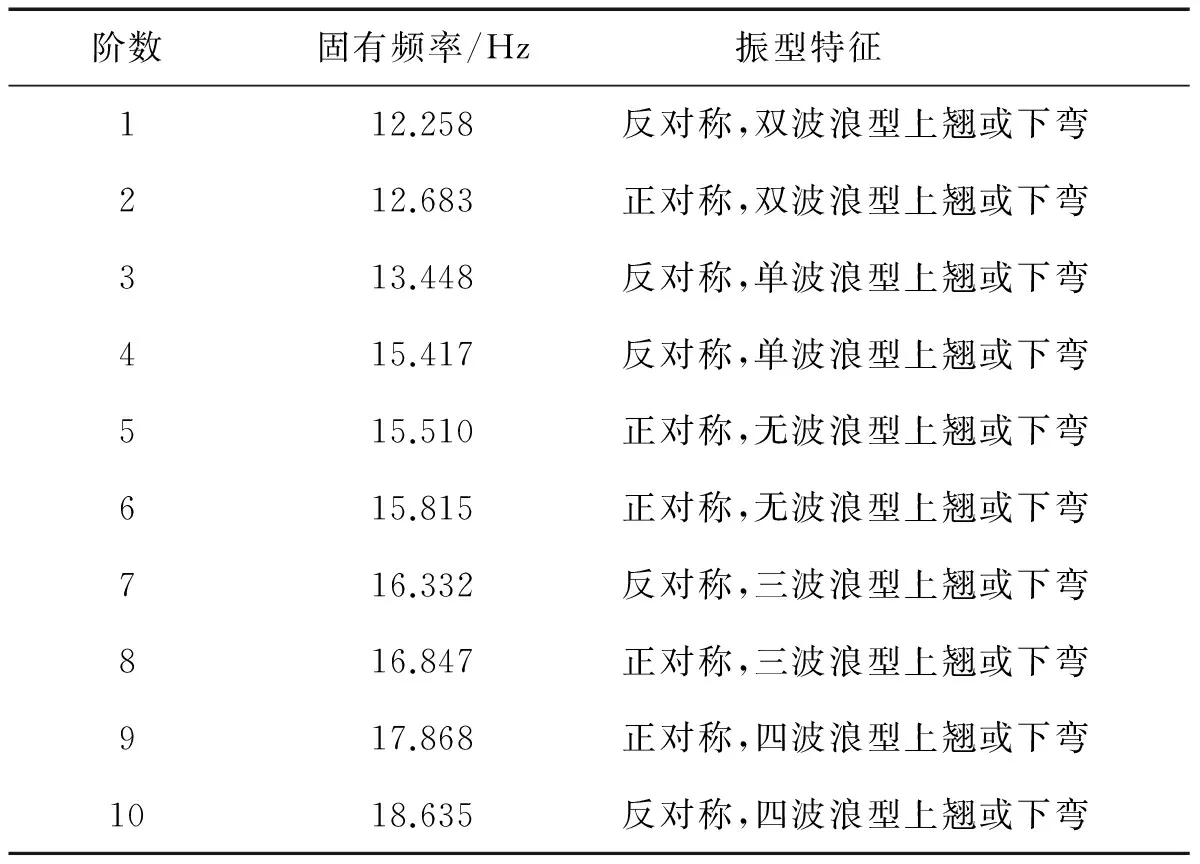
表2 桥梁前十阶自振频率及振型计算结果

5 钢波纹板拱桥的地震时程响应分析

5.1 地震波的选取和输入

本文采用规范标准化地震加速度时程获得地震波，本桥设防烈度为7度，设计基本加速度为0.15g，特征周期为0.4s，场地类别为Ⅱ类，特征周期不需要调整。选用Taft波用于本桥的地震响应分析，所得地震波曲线为图5。根据GB50011—2010(建筑抗震设计规范)知加速度最大值通常按1(水平1)∶0.85(水平2)∶0.65(竖向)的比例调整。本文在输入地震波时选择顺桥向、横桥向、三向叠加三种地震波输入方向。取图2(b)中钢波纹所示控制节点作为地震反应分析的关键位置。

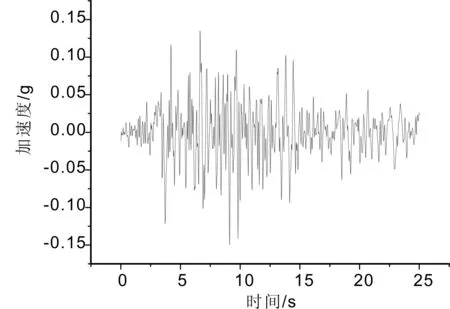
图5 Taft地震波地面加速度时程曲线

5.2 地震激励分析结果

5.2.1 顺桥向地震激励分析结果 在顺桥向地震波激励下，钢波纹板拱桥应力和位移分析结果如图6。

对于位移，顺桥向地震波作用下，该桥出现的位移主要是顺桥向和竖桥向位移，且以顺桥向的位移为主，顺桥向最大位移值为0.213mm,竖桥向最大位移为0.141mm；对于应力，顺桥向地震波作用下，各控制点的最大应力值为2.362MPa。

在顺桥向地震波作用下，多孔波纹板拱桥主要的位移为顺桥向和竖桥向，且以顺桥向的位移为主；在同一拱跨条件下，拱顶的位移要小于1/4拱线的位置，波峰的位移值与波谷的位移是相同的；同一位置，在不同拱跨条件下，中跨的顺桥向位移要小于边跨的顺桥向位移，在拱顶位置，边跨的竖桥向位移大于中跨的竖桥向位移，在1/4拱线的位置，边跨的竖桥向位移值要小于中跨的竖桥向位移，说明在同一拱线上，边跨的竖桥向位移从拱脚向拱顶变化幅度小于中跨的变化幅度。

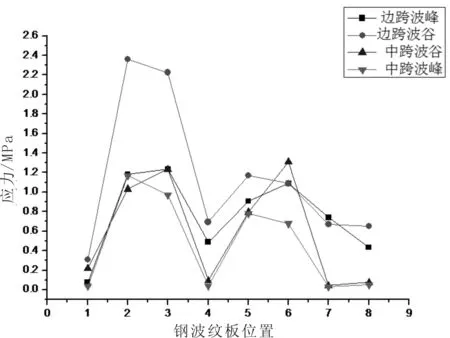
(a) 顺桥向地震作用下各控制点应力值

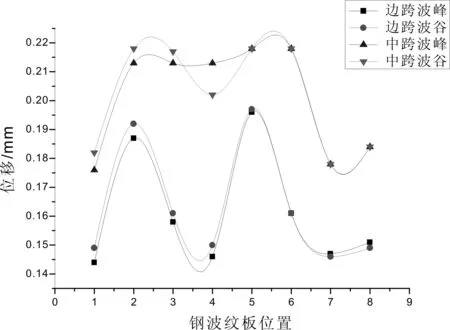
(b) 顺桥向地震作用下控制点顺桥位移值

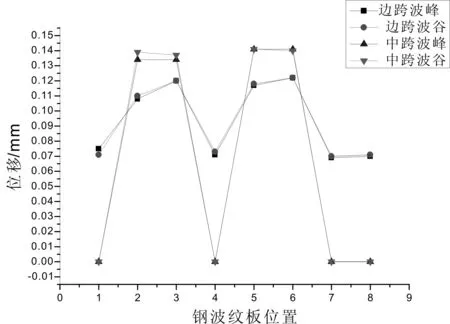
(c) 顺桥向地震作用下控制点竖桥位移值

5.2.2 横桥向地震激励分析结果 横桥向地震波激励下，钢波纹板拱桥应力和位移分析结果如图7。

图7 横桥向地震波应力时程分析结果

在横桥向地震波作用下，钢波纹板桥各控制点位移主要是横向和竖向位移，且钢波纹板桥的位移非常小，最大位移不超过0.1mm；横桥向地震波作用下最大应力值为2.772MPa。在横桥向地震波作用下，钢波纹板桥各控制点位移主要是横向和竖向位移，且钢波纹板桥的位移非常小，最大位移不超过0.1mm，说明钢波纹板桥的横向刚度非常大。

5.2.3 三向地震激励分析结果。在三向地震波激励下，钢波纹板拱桥应力和位移分析结果如图8。

在三向地震波作用下，多孔波纹板拱桥主要的位移为顺桥向和竖桥向，且顺桥向位移较大，横向位移仍不足0.1mm，整个结构最大顺桥向位移值为0.323mm，最大竖桥向位移为0.142mm。在三向地震波作用下最大应力值为3.488MPa。

在三向地震波作用下，多孔波纹板拱桥主要的位移为顺桥向和竖桥向，且顺桥向位移较大，横向位移仍不足0.1mm，说明横向刚度较大，且端部的位移值要小于横向跨中的位移值；在同一拱跨条件下，拱顶的位移要小于1/4拱线的位置，横桥向位移基本一致，波峰的位移值与波谷的位移是相同的；同一位置，在不同拱跨条件下，边跨的位移要大于中跨的位移，顺桥向位移值二者较为接近，且整个结构最大顺桥向位移值为0.323mm，竖桥向位移值二者相差较为明显，最大值为0.142mm，出现在边跨1/4拱线位置。

(a) 三向地震作用下各控制点应力值

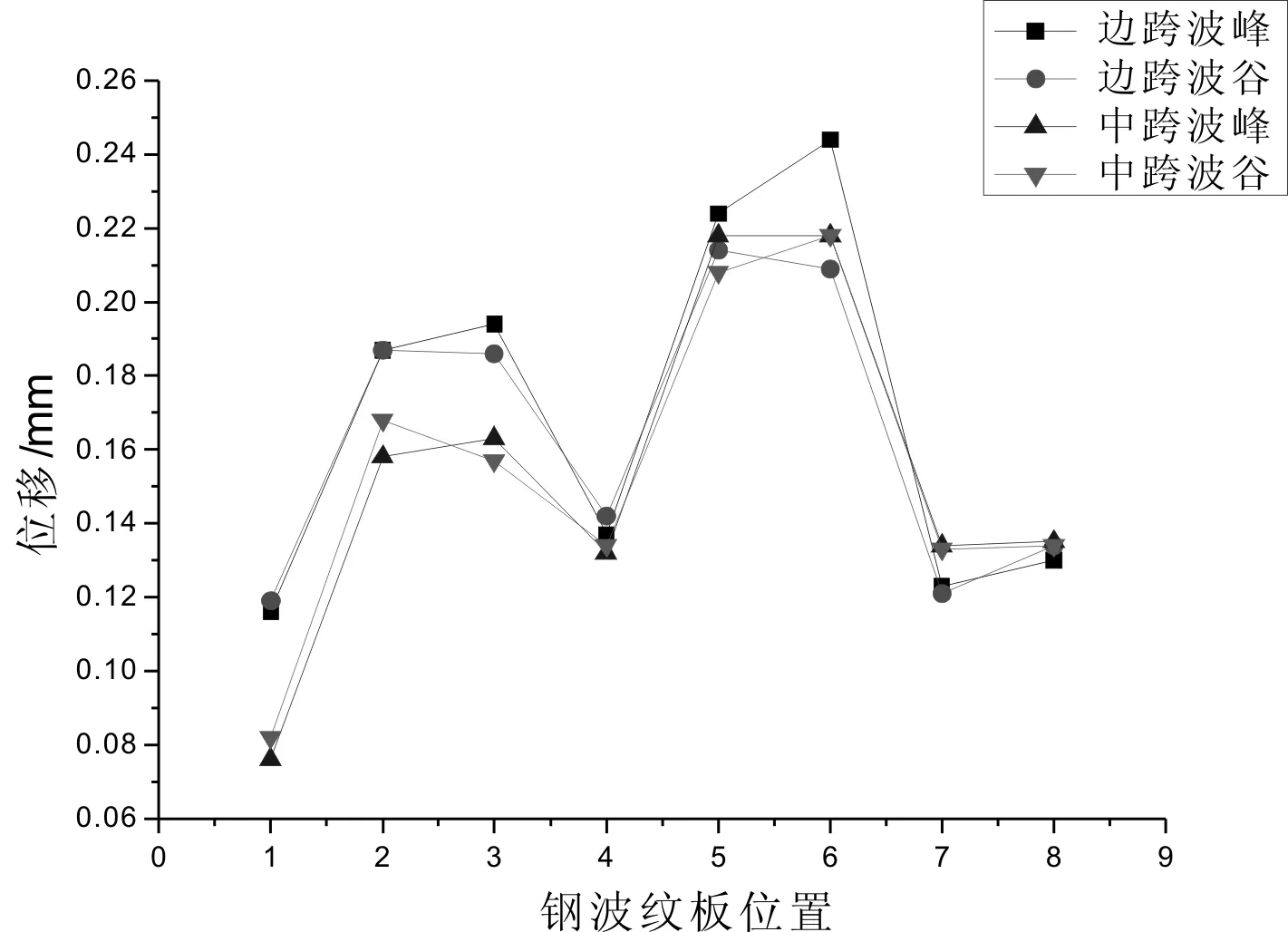
(b) 三向地震作用下控制点顺桥位移值

(c) 三向地震作用下控制点竖桥位移值

6 结 论

依托实际工程，应用有限元软件midas FEA建立钢波纹板拱桥的三维实体模型，通过模拟钢波纹板的实际波形，对该多孔钢波纹板桥进行地震时程响应分析，考虑了顺桥向、横桥向、三向三种方向地震波，得出结论如下。

(1)该桥的结构基频为12.184Hz，表明该桥刚度较大，振型特征主要为两侧桥台上部土体的上翘或下弯振动，与该桥的桥型及场地特性相符。

(2)在同一拱跨条件下，拱顶的位移要小于1/4拱线的位置，对同一个位置相邻的波峰和波谷，位移基本一致。拱顶的顺桥向位移较之四等分点要小29.2%左右，竖桥向位移要小26.3%，横桥向中部位移比端部位移大约5.4%。对于应力，拱顶的应力较之四等分点要小20%左右，横桥向中部应力比端部应力小约10%，同一位置的波峰比波谷应力要小15%左右。说明在同一拱跨条件下，应力和位移响应由拱顶向两侧拱脚处逐渐增大，在拱脚与桥墩连接处应力达到最大。这是由于拱的受力特点决定的，在一个拱圈上，拱脚位置受力最大，受力情况也最为复杂，所以会产生拱脚与桥墩连接处应力最大的现象。

(3)对于不同拱跨，边跨的位移值总是大于中跨的位移值。不同跨的相同位置，顺桥向位移边跨要比中跨大约4.3%，竖桥向位移要大约5.4%。相同位置的应力值，边跨要大于中跨。说明对于不同的拱跨，边跨的地震响应要大于中跨。这是因为中跨两侧所受力和边界条件相同，所以在地震作用下变形与受力曲线关于拱顶轴线基本呈对称性变化规律，而边跨两侧所受情况不同，所以其变形与受力曲线对称性较中跨要差，从而产生二者地震响应不一致的情况。

(4)在三种方向地震波作用下，该多孔波纹板拱桥的横桥向位移均较小，主要是竖桥向及顺桥向振动，说明该多孔钢波纹板桥的横向刚度较大，在抗震设计中应主要考虑竖桥向和顺桥向位移。这是因为该多孔钢波纹板桥的横向刚度较大，在抗震设计中应主要考虑竖桥向和顺桥向位移。

[1] 李祝龙.公路钢波纹管涵洞设计与施工技术研究[D].西安:长安大学公路学院,2006.

[2] 尹航.覆土波纹钢板拱桥力学性能分析及设计方法研究[D].北京.北京交通大学土木建筑工程学院,2008.

[3] National Corrugated Steel Pipe Association.Field Performance Evaluation of Polymer Coated CSP Structures in New York[R].Washington DC:2002.

[4] 李祝龙,刘百来,李自武.钢波纹管涵洞力学性能现场试验研究[J].公路交通科技,2006,23(3):79-82.

[5] 王全录,刘保东,李雨株,等.埋置钢波纹板管涵刚度对其受力性能的影响[J].北京交通大学学报,2012,26(4):1-4.

[6] 刘保东，尹航，王元丰,等. 覆土波纹钢板拱桥施工过程的受力分析[J]. 公路交通科技，2010, 27(1):50-53.

[7] 方诗圣,邹祥强,黄志福,等.地震作用下多孔钢波纹板拱桥力学分析[J].世界桥梁, 2015, 43(3):69-74.

[8] 彭贤明.钢波纹板桥梁结构数值分析[D].广州:华南理工大学土木与交通学院,2012.

[9] 李祝龙,梁养辉,黄志福,等.低路堤荷载作用下钢波纹板拱桥应变的测试研究[J].武汉理工大学学报,2013,31(5):939-942.

[责任编辑：张永军]

Seismic Time History Response Analysis of The Perforated Steel Corrugated Plate Arch Bridge

ZHANG Bai-yong

(Anhui Transport Consulting and Design Institute Co. Ltd.,Hefei 230088, China)

This paper takes the Huaibei section of the highway from Sihong to Xuchang as an example,by using the finite element software FEA Midas, the finite element model is established by simulating the actual ripple shape of the bridge.According to the existing seismic analysis theory,by dynamic time history analysis method,and the seismic waves in three directions, which are along the bridge direction, the transverse direction and the three direction, are considered.The seismic response performance of the bridge is analyzed.The results show，the seismic response (displacement, stress) is most obvious at the arch foot of the same arch.For the different span,the side span near the abutment is more prone to damage.Under the action of seismic waves in three directions,the displacement of bridge direction and vertical direction is more obvious, which should be mainly considered in the design.

corrugated steel plate;arch bridge;actual ripple;time history analysis

2016-06-12 2015-12-20

安徽省交通运输科技项目(ahjtkj2011-012)资助。

张百永，(1977—)，男，河南开封人，安徽省交通规划设计研究总院股份有限公司高级工程师。

U 448.22

A

2096-2371(2016)04-0083-07