基于梯度补偿的分布式电源逆并网逆变器稳定控制

周利骏，李沁愉，赵立骎，夏毅仁

（1.上海合泽电力工程设计咨询有限公司，上海200433；2.国网上海市电力公司市南供电公司，上海 200233）

基于梯度补偿的分布式电源逆并网逆变器稳定控制

周利骏1，李沁愉2，赵立骎1，夏毅仁1

（1.上海合泽电力工程设计咨询有限公司，上海200433；2.国网上海市电力公司市南供电公司，上海 200233）

近年来，由于以分布式光伏发电为代表的新能源发电的快速发展，我国弃风、弃光问题也日益突出，导致这一问题的出现主要原因在于新能源发电技术不够成熟、电能质量较差、无法就地消纳以及可控性、动态稳定性较差。针对分布式光伏发电进行了深入研究，通过构建光伏发电支路的逆变电路模型和引入并网点的电能质量变化梯度补偿的方式，来改进分布式电源并网控制系统的稳态性能。以IEEE16节点算例作为主模型分析了主模型和逆变电路模型的特征根和频域bode图，对比了传统结构和改进后的模型特征根、频域bode图和阶跃响应曲线。结果表明：该方法提升了分布式电源稳定控制性能，改善了控制系统的动态特性。

分布式电源；梯度补偿；动态特性；稳态特性；逆变电路模型

近年来，随着世界能源问题和环境污染问题的日益严重，以光伏发电和风力发电为代表的新能源发电技术引起了越来越广泛的关注和研究[1-2]。现阶段由于分布式发电技术相对不够成熟，以光伏逆变器为主要组成部件的分布式光伏发电电能质量因其自身低惯性、低阻尼的特点，导致起动态响应较快，针对小扰动问题解决能力较差，电能质量相对较低[2]。

针对光伏逆变器自身控制主要有主从控制、下垂控制、V/F控制、P/Q控制等多种控制方法，但是不同控制方法都有不同的显著缺陷[3-5]。PQ/VF控制方法主要应用于同时具备分布式电源并网的模式和分布式电源自发自用的模式下。这种控制方法在不同工作模式稳定运行的情况下，具有控制器稳态误差较小，振荡波动较平缓的特点。但在2种模式的切换过程，尤其是非计划型离网切换中由于需要进行控制器的切换，将导致逆变器调整控制时间较长，易出现电压骤降、骤升和大波动振荡等问题[6-8]。近年来，针对微电网及分布式电源逆变器稳定控制的研究较多，如文献[9-12]通过构建微电网及分布式电源支路的数学模型，并采用根轨迹的方法来分析了微电网及分布式电源的惯性和阻尼系数，具有一定的参考价值。大多数文章仅通过这些方法来提供分布式电源并网对电网系统的稳定性影响分析及建议。文献[13]提出了一种基于多模型预测控制的方法来解决分布式电源逆变器的稳定控制问题，但此方法由于具有多个控制模块切换，并未作多模型控制器的平滑切换处理，势必将因为控制器无法进行无扰切换及灵活调整功率输出而导致分布式电源并网处的母线电压波动震荡，从而导致其输出电能质量下降。

本文主要采用在功率下垂控制的基础上增加母线电压梯度补偿的方法，首先，通过研究分布式电源并网模型以及分布式电源并网点的根轨迹特征根来分析系统的阻尼特征根；其次，通过配置合理的并网点电能质量检测值的梯度变化补偿系数和控制器参数来增加分布式电源在并网点的阻尼系数和惯性系数，优化系统的特征根，从而达到系统应的稳定控制的效果。

1 逆变器模型

逆变器分为三相逆变器和单相逆变器，逆变器底层硬件电路又可划分为单极式和两级式。传统的三相两级式逆变器硬件电路如图1所示。

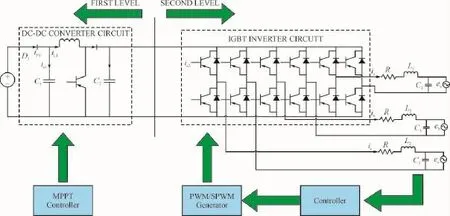
图1 传统三相两级式逆变器硬件电路Fig.1 Hardware circuit of the traditional three-phase two stage inverter

依据Kirchhoff′s回路方程，可对上图1中电路进行模型构建。三相两级式逆变电路数学模型，直流侧电路方程为：

交流侧电路方程如下：

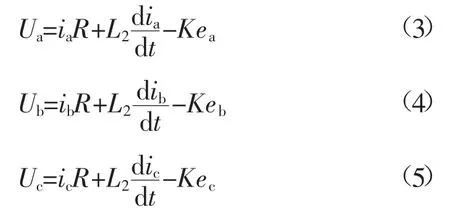
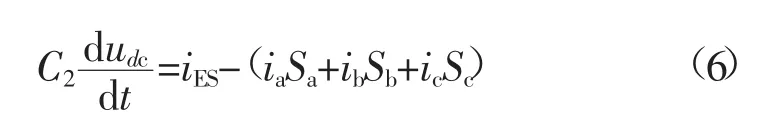
式中：upv为逆变器入口处输入电压；ipv为逆变器注入电流；udc为电容C2两端直流侧电压；Sk为直流侧斩波整流开关电路的开关控制量，经过对Sk进行傅里叶变换分析后，忽略高次谐波影响，可以得到Sk等于晶闸管的占空比；交流侧中Ke表示并网点电网侧母线电压，同直流侧Sk一样，交流侧S表示交流侧晶闸管占空比。

iES表示如下：

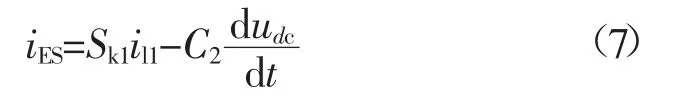
对式（3）至式（6）进行abc-dq0转换可得：

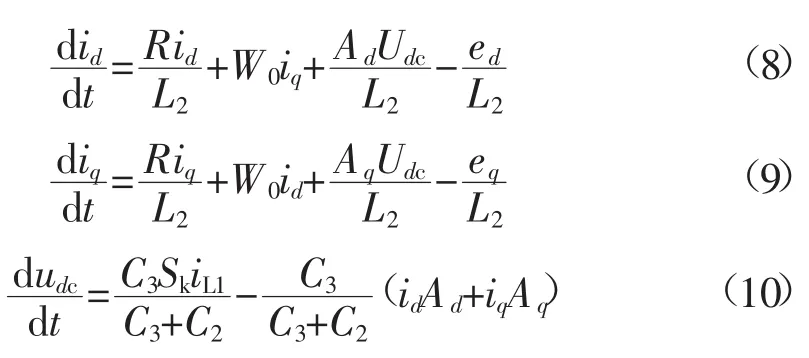
式中：Ad、Aq为Sa、Sb、Sc经过abc-dq0变换后得到的dq分量。通过式（1）、式（2）和式（8）—式（10）可以设逆变器电路的状态空间变量为：

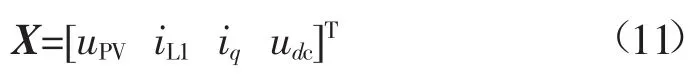
对式（1）、式（2）和式（8）—式（10）进行状态空间模型构建为：

其中输入控制量为：

输出响应量为：

状态空间方程系数为：

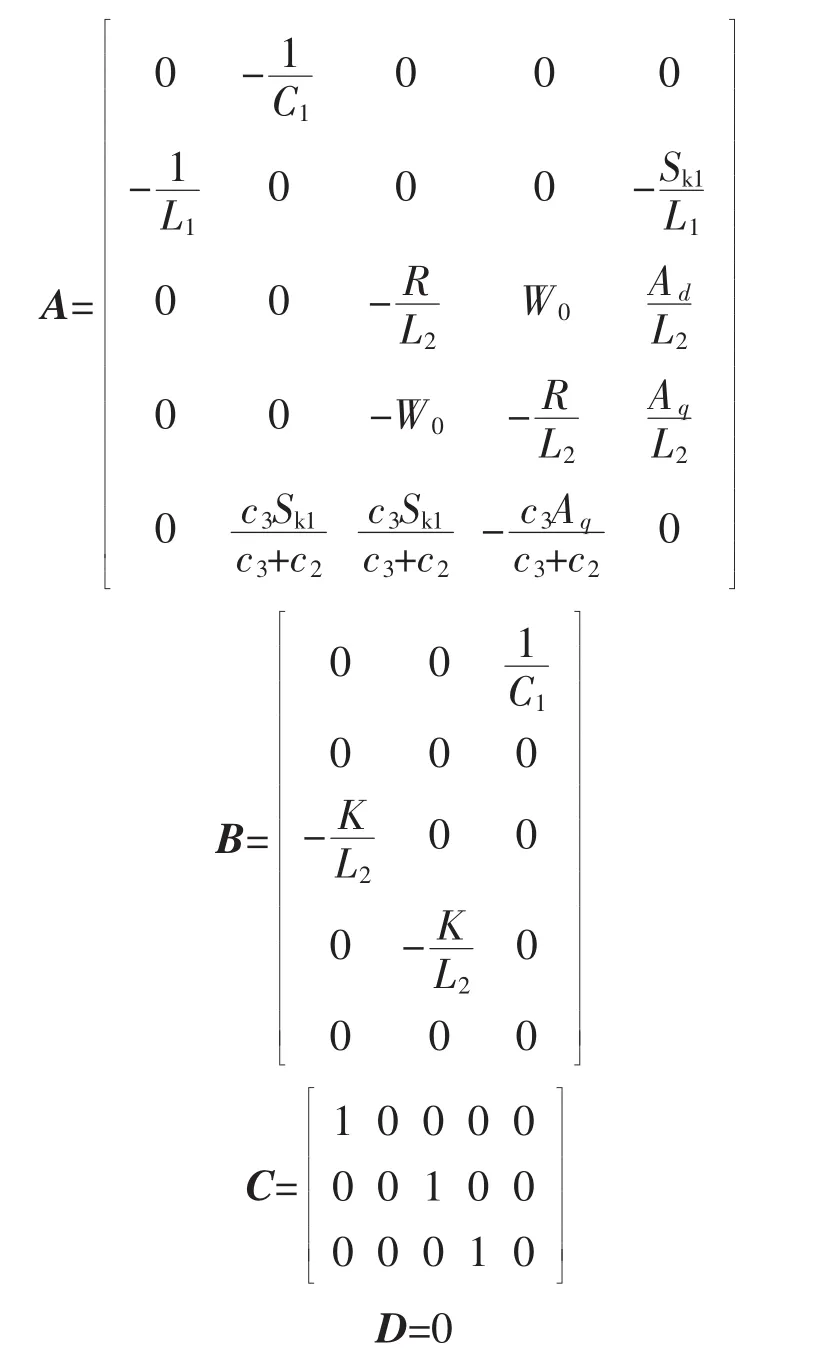
通过对式（12）—式（13）所表述的对象模型进行状态空间和传递函数的变换，可以得到系统对象的传递函数为：

2 控制器设计

逆变电路的对象模型可用传递函数G（s）表示，通过分析G（s）可以看出对象的输出量Vq、Vd存在耦合关系，需对其进行解耦补偿控制。传统功率下垂控制如图2所示，分为PQ控制环路、电压外环控制环路和电流内环控制环路。采用PI控制，系统经过PQ控制器后进入电压外环控制器中，由于电路中存在耦合情况，d轴与q轴重的电压和电流需要分别解耦如式（18）中的wcVq和wcVd作为电压环解耦补偿器，wLIq和wLId作为电流环解耦补偿器。

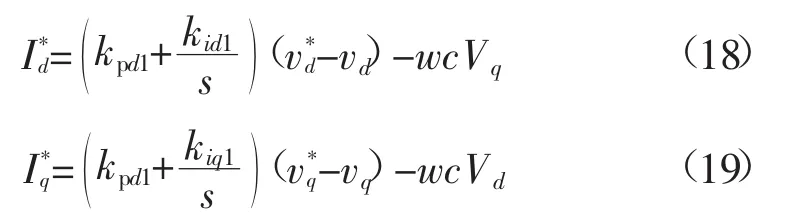
电流环控制方程为：

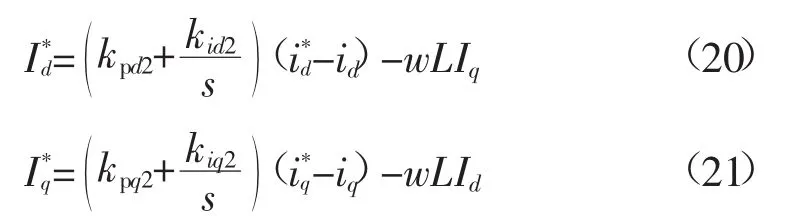
传统PQ控制器内部控制框图如图2所示。这种传统带有电压前馈的PI控制器通常用于电流控制的逆变器中，PI控制器控制灵活可靠，对模型辨识准确度要求不高。但此控制方法具有2个突出的问题：PI控制器跟踪正弦参考信号时会产生稳态误差；当出现干扰信号为周期信号时，由于积分性能差会出现抗干扰能力较差的问题。针对这些问题，采用电压梯度变化前馈补偿的方式进行改进。传统的电流环外引入电压梯度变化补偿如图3所示。

由传统下垂控制中P-F/Q-U的关系可知，d轴梯度变化的检测值为并网点母线频率变化值，而q轴梯度变化的检测值为并网点Ud变化值，并网点电能质量梯度变化率表示为：

将梯度变化率带入图3所示系统中可得d轴和q轴电压偏差表示为：

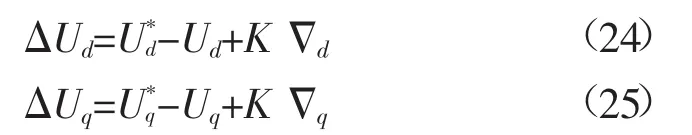
式中：K为补偿系数。

图2 传统PQ控制器内部控制框图Fig.2 Internal control block diagram of the traditional PQ controller

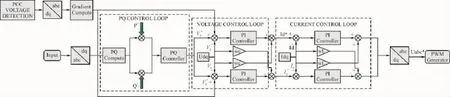
图3 带有梯度补偿的改进控制结构Fig.3 Improved control structure with gradient compensation

3 算例仿真

在文献[14-15]所引用模型的基础上，进行相关仿真研究。采用IEEE16节点改进的微电网模型进行仿真，如图4所示。图4中，节点N3、N13、N6、N9、N15接入分布式微电源。

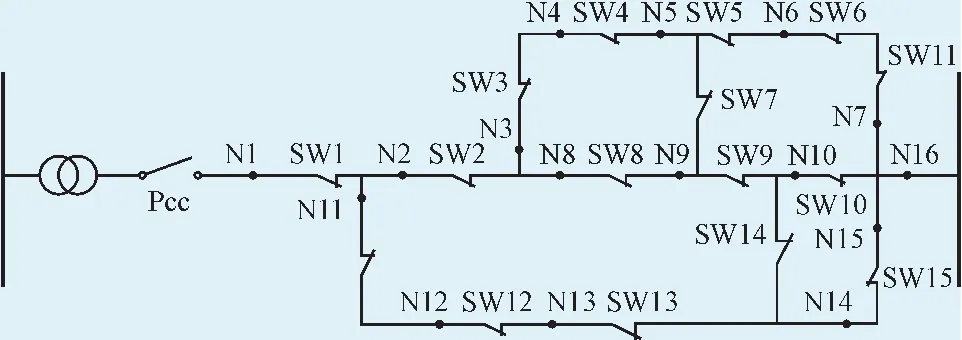
图4 16节点参考模型Fig.4 16 nodes reference model

N3接入发电单元表示为A1，N6接入发电单元表示为A2，N9为接入发电单元表示为A3，N13接入发电单元表示为A4，N15接入发电单元表示为A5。

算例仿真环境为Windows10系统，Matlab 2012a PSAT工具箱。利用PSAT工具箱对系统母线进行根轨迹分析如图5所示。

图5 算例系统的根轨迹图Fig.5 Root locus of a case system

由图5可知，系统存在实轴正半平面特征根，系统不稳定，当系统出现小扰动或者大的冲击干扰时将会出现控制器适配的情况，从而导致系统电能质量较差，甚至分布式电源支路退出系统的情况。为了进一步探究光伏支路的稳定性情况，对光伏支路的逆变电路模型d轴分量模型进行零点极点分析如图6所示，图7为光伏支路逆变电路模型的bode图分析。

图6 光伏支路逆变电路模型的零点、极点分析Fig.6 Analysis of zero and pole of photovoltaic circuit model

图7 光伏支路逆变电路模型的bode图分析Fig.7 Bode diagram analysis of photovoltaic circuit model

由图6可知，系统在实轴负半轴上有1个极点，在需轴正负半轴上有2个极点，其余零点极点均位于原点附近，由图7可知，系统应对干扰冲击稳定能力较弱，系统动态性能较差。需对模型进行零点极点校正设计。对图3所示的逆变器结构中的PI控制器和K进行参数配置。如图8和图7所示分别为配置的控制系统校正后的零极点图和bode图。

对比图6—图9可知，系统在进行补偿和PI控制器重新校正设计后动态性能明显改善。如图10所示为原系统模型解耦后d轴和q轴的阶跃响应曲线，如图11所示为进行补偿和参数校正配置后系统的d轴和q轴阶跃响应曲线。

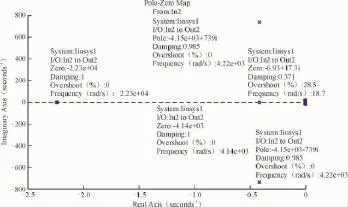
图8 校正设计后的光伏支路逆变电路模型的零点极点图分析Fig.8 Pole figure analysis of the model of the PV circuit model after correction design

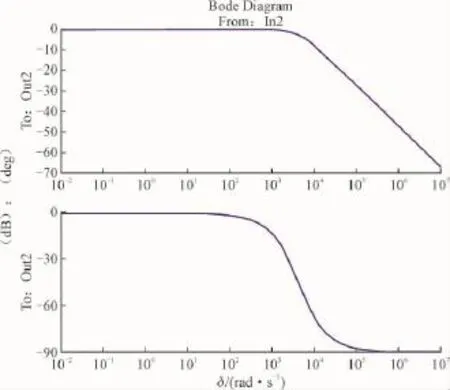
图9 校正设计后的光伏支路逆变电路模型的bode图分析Fig.9 Bode diagram analysis of the PV circuit model after calibration design

由图10、图11可知，原系统解耦后的d轴q轴的阶跃响应的调节时间分别为0.44 s和0.554 s，进行梯度补偿和参数校正配置系统解耦后的d轴和q轴的阶跃响应调节时间分别为0.003 97 s和0.019 s。通过图10和图11对比可知，经过梯度补偿和校正配置后的系统阶跃响应速度得到大幅提升，系统的稳态性能和动态性能得到改善。

并网点N3处接入分布式光伏电源后的电压输出曲线如图12所示。并网点输出电流如图13所示。并网点N3调整过程中有功功率检测曲线如图14所示。

4 结语

本文在传统的控制结构中引入并网点电能质量检测值梯度变化补偿的方法，使用带有分布式电源的IEEE16节点模型进行了特征根求取和根轨迹分析，说明了IEEE16节点系统在引入分布式光伏发电支路后动态性能较差。为了探究影响系统的主要因素，对光伏支路的逆变电路模型进行了特征根分析和频域Bode图分析，再次验证了传统分布式电源的动态性能较差，通过使用提出的并网检测值梯度变化补偿和根据逆变电路模型的特征根和频域Bode图进行控制系统校正配置后，再次进行了特征根和频域仿真分析验证。由实验结果可知，改进后的系统动态响应时间更快，系统阻尼特性得到改善，系统动态性能得到明显提升。通过光伏支路的电压、电流、及功率仿真输出曲线可以看出系统的动态性能得到明显提升。通过功率调节曲线和电压曲线的分析可以看出系统仍然存在稳态误差和震荡的情况，这是由于控制结构中PI控制器自身在进行控制过程中具有稳态误差和震荡的特性导致的。本文的下一步工作将是进行PI控制器研究并尝试寻找一种新型控制器来取代PI控制器从而消除稳态误差和震荡。

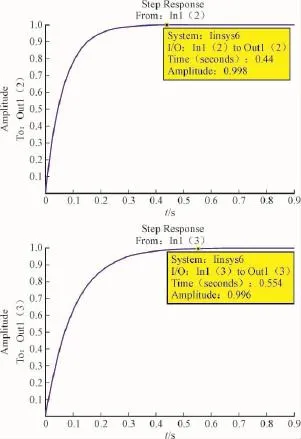
图10 原系统模型解耦后d轴和q轴的阶跃响应曲线Fig.10 The step response curves of the d and q axes after decoupling of the original system model

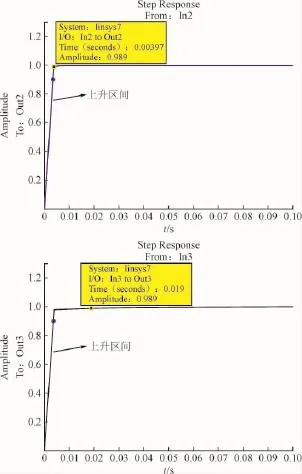
图11 梯度补偿和参数校正配置后系统解耦后d轴和q轴的阶跃响应曲线Fig.11 The step response curves of the d and q axes after the decoupling of the system after the gradient compensation and the parameter correction

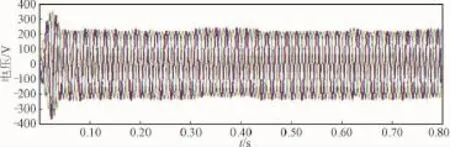
图12 并网点N3分布式光伏电源输出电压曲线Fig.12 Distributed PV power output voltage curve of the grid connection point N3

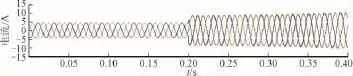
图13 并网点N3分布式光伏电源输出电流曲线Fig.13 Distributed PV power output current curve of the grid connection point N3

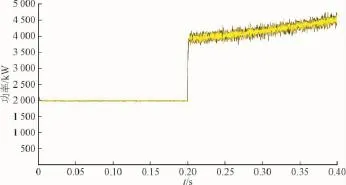
图14 并网点N3分布式光伏电源输出有功功率调节曲线Fig.14 Output active power regulation curve of distributed photovoltaic power supply of the grid connection point N3

[1]朱珺敏，李鹏，王阳，等.基于改进下垂特性的微网功率控制方法[J].电网与清洁能源，2012，28（6）：29-33.ZHU Junmin，LI Peng，WANG Yang，et al.Micro-grid power control method based on improved droop characteristics[J].Power System and Clean Energy，2012，28（6）：29-33（in Chinese）.

[2]杨仁花，黄伟，关丽，等.微网结构和运行控制[J].电网与清洁能源，2010，26（1）：48-55.YANG Renhua，HUANG Wei，GUAN Li，et al.Structure and operation control of micro-grids[J].Power System and Clean Energy，2010，26（1）:48-55（in Chinese）.

[3]申展，胡辉勇，雷金勇，等.分布式电源接入用户及用户侧微电网双向电能计量问题[J].南方电网技术，2015，9（4）:14-21.SHEN Zhan，HU Huiyong，LEI Jinyong，et al.Bidirectional metering issues of user side microgrid and user with distributed generation[J].Southern Power System Technology，2015，9（4）:14-21（in Chinese）.

[4]柳岩妮，公茂法，王来河，等.基于混沌优化蝙蝠算法的含分布式电源配电网故障区段定位[J].电力科学与工程，2016，32（8）:11-15.LIU Yanni，GONG Maofa，WANG Laihe，et al.Fault location of distribution network with distributed generation based on chaos optimization algorithm[J].Dlkxygc，2016，32（8）:11-15（in Chinese）.

[5]唐劲飞.分布式电源并网运行的有功无功解耦控制研究[D].北京：华北电力大学，2007.

[6]YU Kai，AI Qian，WANG Shiyi，et al.Analysisi and optimization of droop controller for microgrid system based on small-signal dynamic model[J].IEEE Transactions on Smart Grid，2016，7（2）:695-705.

[7]龚新平.几类线性系统的容错控制器设计方法研究[D].哈尔滨：哈尔滨工程大学，2012.

[8]索江镭，胡志坚，张子泳，等.含风电场的互联电力系统辨识与广域时滞阻尼控制器设计[J].电力系统自动化，2014，38（22）：17-25.SUO Jianglei，HU Zhijian，ZHANG Ziyong，et al.Identification and wide-area damping controller design of interconnected power systems containing wind farms[J].Automation of Electric Power Systems，2014，38（22）：17-25（in Chinese）.

[9]FIDA HASAN MD RAFI，JAHANGIR HOSSAIN，LU Junwei.PV microgrid islanded operation analysis with the designed smart VSI.[C].2015 ieee 10th Conference on Industrial Electronics and Applications（ICIEA）.2015:632-637.

[10]ORTEGA R，CARRANZA O，SOSA J C，et al.Applicationg control configurations for parallel connection of single-phase energy conversion units operating in island mode[J].America Transactions，2016，14（2）:694:703.

[11]YU Kai，AI Qian，WANG Shiyi，et al.Analysis and optimization of droop controller for microgrid system based on small-signal dynamic model[J].IEEE Transactions on Smart Grid，2016，7（2）:695-705

[12]殷晓刚，戴冬云，韩云，等.交直流混合微网关键技术研究[J].高压电器，2012，48（9）:43-45.YIN Xiaogang，DAI Dongyun，HAN Yun，et al.Discussion on key technologies of AC-DC hybrid microgrid[J].High Voltage Apparatus，2012，48（9）:43-45（in Chinese）.

[13]SNEHA MANE，PUSHPAK JAGTAP，FARUK KAZI，et al.Model predictive control of complex switched mode FCUC hybrid structure[C].2016 Indian Control Conference，2016:66-71.

[14]艾欣，邓玉辉，黎金英．微电网分布式电源的主从控制策略[J]．华北电力大学学报（自然科学版），2015，42（1）: 1-6.AI Xin，DENG Yuhui，LI Jinying.Master-slave control strategy for distributed generation microgrid[J].Journal of North China Electric Power University，2015，42（1）:1-6（in Chinese）.

[15]董润楠，曹剑馨，梁庚.基于有色Petri网的微电网被动式孤网控制方法研究[J].电网与清洁能源，2013，29（12）:16-21，29.DONG Runnan，CAO Jianxin，LIANG Geng.Studies on the control method for the passive islanding of the migrogrid based on colored petri net[J].Advances of Power System&Hydroelectric Engineering，2013，29（12）:16-21，29（in Chinese）.

（编辑 董小兵）

Stability Control of Grid-Connected Inverter of Distributed Generation Inverse Grid Based on Gradient Compensation

ZHOU Lijun1，LI Qinyu2，ZHAO Liqin1，XIA Yiren1
（1.Shanghai Heze Power Engineering Design&Consulting Co.，Ltd.，Shanghai 200433，China；2.Shinan Power Supply Company of SMEPC，Shanghai 200233，China）

With rapid development of distributed photovoltaic power generation representative of new energy power generation in recent years，the problem of abandoned wind，abandoned photovoltaic has become increasingly prominent in China.The problem can be attributed to immature new energy power generation technology，poor power quality，difficult local consumption，poor controllability and dynamic stability.This paper presents an in-depth research into distributed photovoltaic power generation.By constructing the inverter circuit model of photovoltaic power generation branch and introducing the power quality variation gradient compensation method，the steady-state performance of the grid connected control system is improved.Furthermore，the paper uses the IEEE16 node as the main model to analyze the characteristic root and frequency domain Bode diagram of the main model and the inverter circuit model.By comparing the characteristic root，frequency domain Bode diagram and step response curve of the traditional structure and the improved model it is proved that this method can improve the control performance of the distributed power supply，and improve the dynamic charac-teristics of the control system.

distributed generation；gradient compensation；dynamic characteristics；steady state characteristics；inverter circuit model

国家高技术研究发展计划（863）项目（2015A A050600）。

Project Supported by the National High Technology Research and Development Program of China（863）（2015AA050600）.

1674-3814（2016）10-0146-07

TM464；TM61

A

2016-06-20。

周利骏（1978—），男，本科，工程师，从事配电网技术研究及管理工作。