考虑装配误差的重载面齿轮传动啮合性能分析

王延忠, 刘元鹏,吴玉广，刘 文

(1.北京航空航天大学 机械工程及自动化学院，北京 100191；2.中国兵器工业新技术推广研究所，北京 100089)



考虑装配误差的重载面齿轮传动啮合性能分析

王延忠1, 刘元鹏1,吴玉广2，刘 文1

(1.北京航空航天大学 机械工程及自动化学院，北京 100191；2.中国兵器工业新技术推广研究所，北京 100089)

针对实际应用中的重载面齿轮传动接触轨迹分析较为复杂，不仅包括初始装配误差，还有重载作用下支承系统的变形等，引入载荷当量安装调整值概念，利用解析法和有限元方法分别将重载作用下支承轴、轴承和箱体的变形转化为初始装配误差，通过推导考虑装配误差的面齿轮传动接触轨迹的方程组进行计算，并将其进行可视化处理，得到了面齿轮传动接触轨迹随着不同载荷变化的移动规律，为面齿轮传动接触轨迹的精确可控及预测提供了参考依据。

装配误差；载荷当量安装调整值；解析法；有限元方法；接触轨迹

面齿轮传动作为一种新型的动力传动，与传统的螺旋锥齿轮传动相比，具有承载能力高、体积小、质量轻、噪声低和传动平稳等优点，在航空、TK传动等领域有着越来越广泛的应用[1]。在面齿轮传动过程中，在小齿轮与面齿轮相互啮合的轮齿表面留下一系列瞬时接触点，同一齿面上的各个瞬时接触点的集合构成了齿面接触迹。接触迹的位置、形状和大小是影响面齿轮传动副承载能力、振动噪声和工作寿命等传动性能的关键因素，同时也是反映面齿轮制造和安装精度的重要指标[2]。对于重载工况下的面齿轮传动，由于载荷较大，小齿轮与面齿轮的支承系统会发生相对较大的形变，使得传统的理论接触区的计算结果与实际情况相差很大。

国外学者Krenzer在M.L.Baxte[3]、Litvin等研究的基础上，通过改进刚性齿面接触的假设，提出了在轻载作用下的齿面承载接触分析(Loaded Tooth Contact Analysis，LTCA)[4]。在国内，重庆大学的郑昌启教授等[5]提出了弧齿锥齿轮的接触应力分析法；中南大学的曾韬教授[6]分析了螺旋锥齿轮多种不良形式的接触区并给出修正方法；西北工业大学的方宗德教授[7]主要对齿轮的加载接触分析进行了研究，并得出了一些有指导意义的结论；中南大学的唐进元教授等[8]综合考虑齿轮的制造误差及装配误差等因素，提出了一种考虑误差的E-TCA分析方法，使得齿面接触区域的理论分析更加贴近实际情况。上述学术成果都为本文提供了理论基础。

1 含装配误差的无载面齿轮传动接触轨迹的理论计算

面齿轮传动过程中的装配误差主要分为3种：1)轴交角误差，即两齿轮轴线之间的夹角误差Δγ；2)轴交错误差，即两齿轮轴线交错而不相交，之间的最小距离Δe；3)轴向偏移误差，即面齿轮沿本身轴线方向位移Δz。

本文以正交面齿轮为例进行分析。在已知小齿轮和面齿轮齿面(∑P和∑F)分别在固联在两齿轮上的坐标系(SP和SF)中的方程的前提下，根据如图1所示的含装配误差的面齿轮与无装配误差面齿轮坐标系之间的转换关系，即可求出含装配误差的面齿轮传动接触轨迹的方程。

对于共同的固定不变的坐标系SP0来说，两齿面在接触点处具有相同的位置向量和法向量，即：

(1)

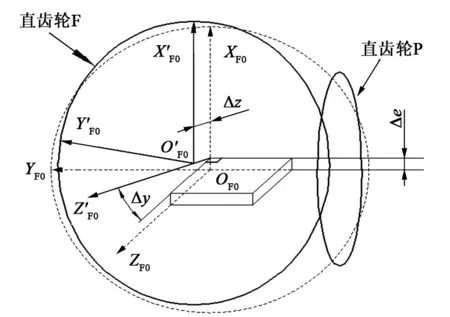
图1 正交面齿轮中装配误差的描述

根据式1以及坐标系之间的转换关系，最终可求出含装配误差的面齿轮传动接触轨迹的方程：

(2)

(3)

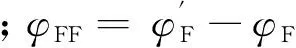
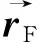
2 重载面齿轮传动接触轨迹的计算

在重载面齿轮传动中，影响齿面接触轨迹的因素不仅有初始装配误差，还包括重载作用下面齿轮支承系统和轮齿自身的变形。其中，轮齿的弹性变形和弯曲变形对齿轮啮合位置影响很小，因此轮齿啮合接触轨迹的变化可以看成是由初始装配误差和支承系统的变形引起的。支承系统的变形又包括支承轴、轴承的变形和箱体的变形。为了能够计算出变形对啮合接触轨迹的影响，引入载荷当量安装调整值概念，将2种变形分别通过解析法和有限元法等效到初始装配误差上，得到载荷作用下面齿轮传动接触轨迹的变化趋势。

2.1 支承轴、轴承变形的当量化

建立面齿轮传动支承系统的弹性变形坐标系(见图2)，其中，坐标系Osliljlkl和 Osrirjrkr分别在小齿轮和面齿轮的轴线上，kl轴和kr轴分别沿着小齿轮和面齿轮的轴线方向，il轴和ir轴分别从各自坐标系的原点指向啮合点M(x,y,z)。

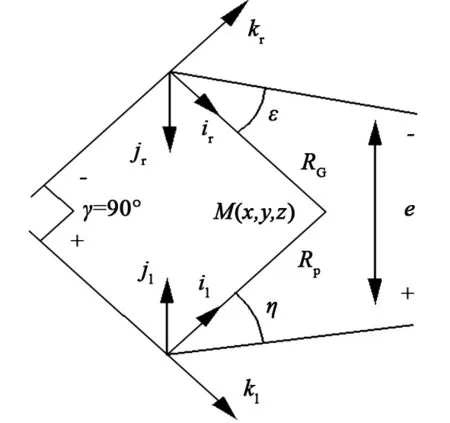
图2 面齿轮传动系统弹性变形坐标系

设小齿轮支承轴的扭转变形为Δφf，弯曲变形为fxf、fyf，轴向变形为fzf，支承轴承的变形分别为δxf、δyf和δzf；面齿轮的支承轴的扭转变形为Δφq，弯曲变形为fxq、fyq，轴向变形为fzq，支承轴承的变形分别为δxq、δyq和δzq。若将面齿轮副的支承轴、轴承在载荷作用下的变形所引起的误差等效到轴交错误差Δe和轴交角误差Δγ上，则有：

Δe1=

(RGΔφq+fxq+δxq)cosε+(fyq+δyq)sinε+

(fyf+δyf)sinη+(RPΔφf+fxf+δxf)cosη

(4)

Δγ1=

(5)

式中，RP和RG分别为小齿轮和面齿轮在啮合点M的半径；η和ε分别为小齿轮和面齿轮在啮合点M的偏置角。

载荷作用下小齿轮和面齿轮支承轴的变形可以通过材料力学的相关理论计算得出。而轴承的变形可以根据文献[9]计算得出。将支承轴和轴承的变形带入式4和式5，即可计算出载荷作用下支承轴和轴承变形的当量装配误差。

2.2 箱体变形的当量化

从社会的角度看，书法休闲活动有雅玩怡情功能，促进和谐稳定的功能。社会分工细化，日趋紧张忙碌，人们的休闲意愿日益强烈，通过书法作为休闲活动的载体，在书法活动中书写自我，雅玩怡情，在书法活动中结识新朋友，使在紧张的工作中产生的一部分不良情绪通过一种书法休闲活动得到很好释放，去除疲劳，并以更饱满的精神投入到工作学习中去。从整个社会的角度讲，书法休闲活动有利于促进社会的和谐稳定。

面齿轮箱体在传递扭矩过程中轴承孔会发生变形，进而产生轴线方向的误差，这种误差会对面齿轮副的啮合产生影响。

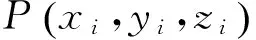
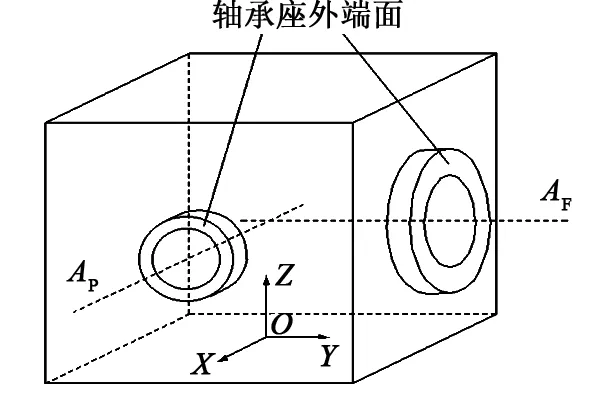
图3 面齿轮箱体结构示意图

若将箱体的变形等效为装配误差，设小齿轮和面齿轮支承轴长度分别为LP和LF，箱体变形前后的小齿轮轴线在XY平面和XZ平面的夹角分别为αP1和αP2，面齿轮轴线在XY平面和YZ平面的夹角分别为αF1和αF2，则有：

Δe2=αP2LP+αF2LF

(6)

Δγ2=αP1+αF1

(7)

载荷作用下面齿轮箱体的变形可以通过有限元方法计算得出，将得出的变形量带入到式6和式7中，即可计算出载荷作用下箱体变形的当量装配误差。

2.3 载荷作用下接触迹的计算

在重载面齿轮传动中，包含初始的装配误差(Δe0,Δz0,Δγ0)、支承轴和轴承变形的当量装配误差(Δe1,Δγ1)以及箱体变形的当量安装误差(Δe2,Δγ2)，则重载面齿轮传动的无载当量装配误差为：

(8)

将式8带入式2中，求解方程组，即可计算出重载面齿轮的接触迹。

3 实例分析

建立面齿轮接触迹计算分析数学模型，参数见表1。

表1 面齿轮传动系统参数

3.1 轴和轴承变形当量安装误差的计算

根据已建立的数学分析模型，通过2.1小节给出的方法，可计算出给定载荷作用下轴和轴承变形的当量装配误差Δe1和Δγ1。

3.2 箱体变形当量安装误差的计算

建立面齿轮传动参数对应箱体的模型，并导入ABAQUS中，给定载荷和约束及边界条件，计算出箱体的变形。载荷为1 000 N·m时箱体的变形如图4所示。将箱体节点进行编号(见图5)，并提取出变形后轴承座外端面各节点的坐标(见图6)，根据2.2小节给出的方法，可计算出箱体变形的当量装配误差Δe2和Δγ2。

图4 面齿轮箱体的变形云图

图5 箱体节点编号

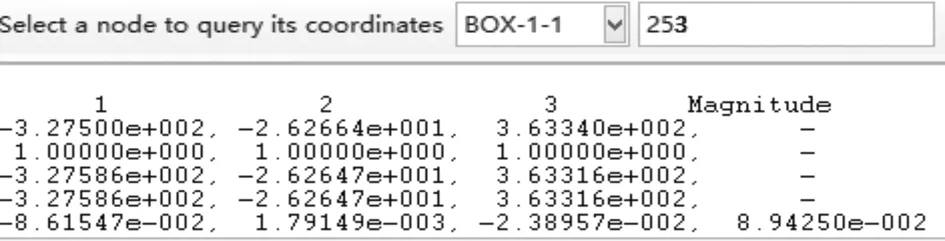
图6 提取变形后节点坐标

3.3 不同载荷作用下的接触迹

设初始装配误差Δe0、Δz0、Δγ0均为0，则面齿轮传动接触迹的变化完全是由支承系统的弹性变形引起的，即Δe=Δe1+Δe2，Δγ=Δγ1+Δγ2，则可得到根据给定参数所建立的面齿轮分析模型在不同载荷作用下的当量装配误差(见表2)。

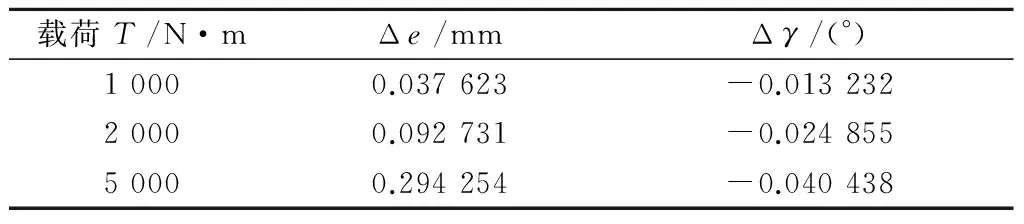
表2 不同载荷作用下的当量装配误差

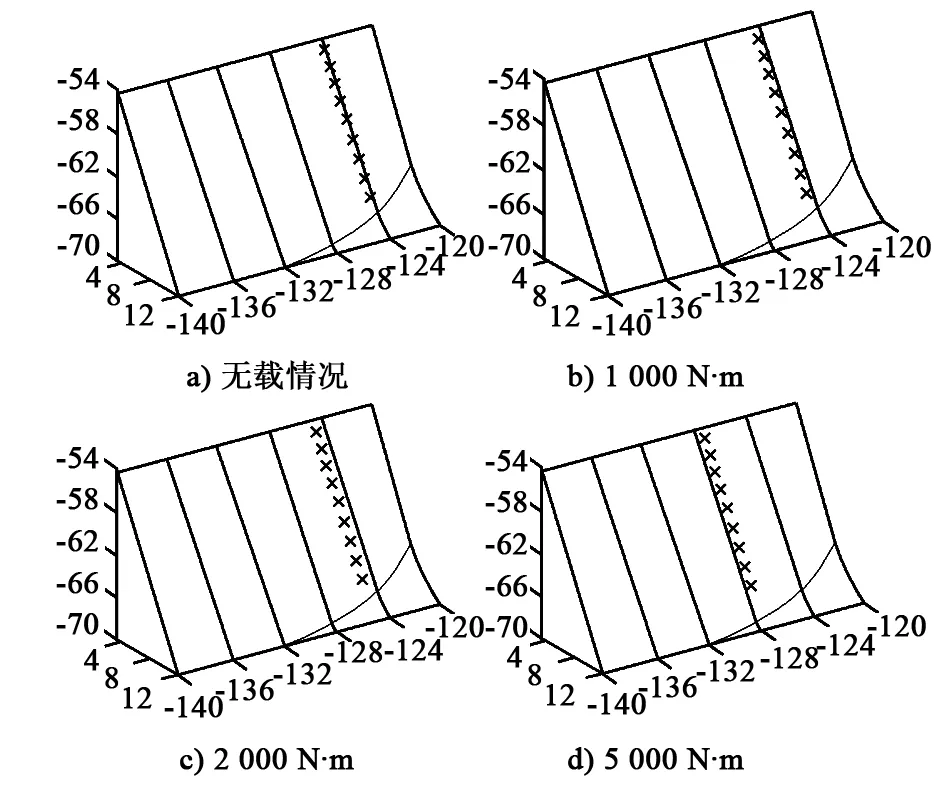
图7 不同载荷作用下的接触迹

面齿轮上接触迹的可视化如图7所示，齿宽方向上接触迹位置的平均值与载荷的关系如图8所示。由图7、图8可知，重载面齿轮传动接触迹随着载荷的增大具有向着外径方向移动的趋势，并且移动幅度越来越大。面齿轮的齿厚沿着外径方向逐渐减小，这就使得面齿轮的承载能力受到影响，可通过面齿轮齿面修型等方法解决这一问题，使接触迹接近理论位置。

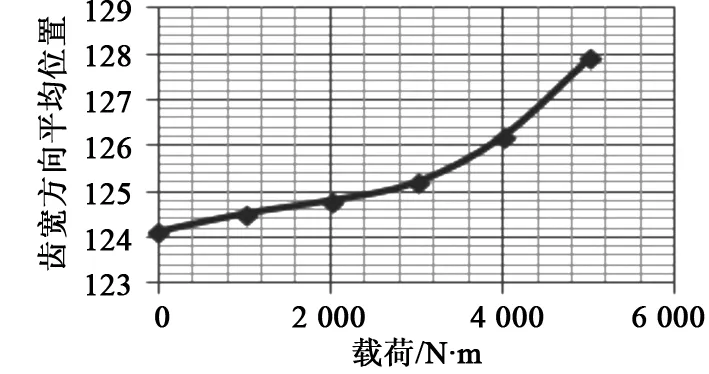
图8 接触迹位置随载荷变化曲线

4 结语

1) 本文通过解析法将重载面齿轮副支承轴和轴承的变形当量化，将几何分析与力学分析有机地结合在一起进行面齿轮加载接触分析，等效到装配误差上进行接触迹的计算。

2)利用有限元分析计算出载荷作用下箱体的变形，并将其当量为装配误差进行接触迹的计算。

3)计算得到不同载荷对重载面齿轮接触轨迹的影响机理和变化趋势，使理论分析结果更加接近实际情况，为重载面齿轮传动装调技术提供了理论依据。

[1] 戈红霞,吕庆军,张志凯.关于面齿轮接触和弯曲应力有限元计算方法的研究[J]. 新技术新工艺,2014(1):43-47.

[2] 吴灿辉,王延忠.产品几何技术规范(GPS)在面齿轮齿面检测中的应用[J].新技术新工艺,2012(7):91-93.

[3] Baxter M L. Basic geometry and tooth contact of hypoid gears [J]. Industrial Mathematik，1961(11) : 19-28.

[4] Krezer T J. Tooth contact analysis of spiral bevel and hypoid gears under load[R]. New York: Gleason Works Publication, 1981.

[5] 黄昌华,郑昌启,吕传贵.螺旋锥齿轮加载接触分析计算原理[J].机械工程学报，1993, 29(4):50-54.

[6] 曾韬.螺旋锥齿轮设计与加工[M].哈尔滨:哈尔滨工业大学出版社,1989.

[7] 方宗德.修形斜齿轮的承载接触分析[J].航空动力学报,1997,1(3) :251-254.

[8] 唐进元,卢延峰,周超.有误差的螺旋锥齿轮传动接触分析[J].机械工程学报,2008, 44(7) :16-23.

[9] 邓四二,贾群义.滚动轴承设计原理[M].北京：中国标准出版社，2008.

责任编辑 马彤

Meshing Performance Analysis of Face Gear Drive under Heavy Load with Assembly Error

WANG Yanzhong1, LIU Yuanpeng1, WU Yuguang2, LIU Wen1

(1.School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China; 2.Advanced Technology Generalization Institute of CNGC, Beijing 100089, China)

Analysis of contact path in face gear drive under heavy load is complicated in practical application including key factors such as initial assembly error and deformation of the support system. Deformation of support axis and bearings, and deformation of gearbox are transformed into the initial assembly error by introducing the concept of load equivalent assembly adjustment value. Use the analytical method and finite element method respectively. Finally, there comes out several of contact path in face gear drive under the different load by calculating the equation set on contact path with assembly error of face gear transmission, and provide reference frame for controlling contact path accurately.

assembly error，load equivalent assembly adjustment value，analytical method，finite element method，contact path

TH 132.2

A

王延忠 (1963-),男，教授，博士生导师，主要从事先进精密传动加工技术、空间啮合曲面加工理论及应用技术等方面的研究。

2016-04-06