单模光纤中GVD和SPM产生的啁啾及影响

樊林林，乔记平

(太原理工大学 a.物理与光电工程学院,b.电气与动力工程学院，太原 030600)



单模光纤中GVD和SPM产生的啁啾及影响

樊林林a，乔记平b

(太原理工大学 a.物理与光电工程学院,b.电气与动力工程学院，太原 030600)

利用理论推导总结了频率啁啾的概念,以非线性薛定谔方程为基础,用数值模拟方法研究了群速度色散(GVD)和自相位调制(SPM)作用下啁啾的产生以及对光脉冲传输的影响,得出了GVD和SPM两种效应所致啁啾的产生机理不同,其结果对于光纤中脉冲传输特性的研究具有重要的意义。

频率啁啾；群速度色散；自相位调制；光孤子

光脉冲在光纤的传输过程中,由于光纤色散效应的存在,导致光脉冲的时域展宽,限制了光脉冲的传输距离,并降低光通信的传输速率,通常对脉冲展宽起主要作用的是群速度色散[1]。由于GVD效应的存在,超短光脉冲在光纤中的传播具有与长脉冲传播极为不同的特性,而一般光纤的长度都较长,由此产生的SPM效应也十分明显。所以在光纤中,GVD效应与SPM效应成为决定超短光脉冲传播特性的两个最基本的因素,而频率啁啾在这两种效应中对光脉冲的传输特性又有很重要的作用[2-3]。本文总结了频率啁啾的概念, 以非线性薛定谔方程为基础,数值模拟研究并讨论了GVD和SPM两种效应下啁啾的产生及其对脉冲传输的影响[4-12],最后比较了两者产生啁啾的不同。

1 理论分析

1.1 频率啁啾

假设脉冲的瞬时频率随时间t的表达式为:

(1)

式中：ω0为不考虑非线性效应时的载波频率；ω′(t)为与时间有关的非线性引起的频率。用δω(t)代替ω′(t)并整理得:

(2)

式中,δω(t)为瞬时频率与载波频率的差,称为频率啁啾量,简称啁啾。则式(1)变为:

(3)

由式(3)知,由于随时间变化的δω(t)的存在使光脉冲不同的部位有不同的瞬时频率,也就是说脉冲在介质中传播时频率得到调制,这种调制即为啁啾。

现在由自相位调制来推导啁啾表达式。由于相移φ和折射率n满足下式:

(4)

式中：k0=2π/λ0；z为传播距离,随时间变化的折射率n由下式决定:

(5)

(5)式右边第一项是线性的,第二项是与光强有关的非线性项,其中n1为非线性折射率系数。将式(5)代入式(4)得到相移为:

(6)

上式中已令δφNL(t)=n1|E(t)|2k0z.

由频率与相移的关系有:

(7)

与式(3)比较有

(8)

式中，“-”是由于E(t)中取e-iω0t.

啁啾参量是描述频率变化的物理量,把频率随时间的变化率定义为啁啾参量。对自相位调制有:

(9)

c(t)>0为正(或上)啁啾,脉冲的瞬时频率随时间增加。c(t)<0为负(或下)啁啾,脉冲的瞬时频率随时间减小。可见,啁啾参量的正负与啁啾量的正负是不同的。

1.2 啁啾的产生及其影响

脉冲通过单模光纤传输需要满足的非线性薛定谔方程为:

(10)

式中：U(z，T)为归一化振幅；z为脉冲传输距离；β2为群速度色散系数；t为延迟时间；α为光纤损耗系数；γ为非线性系数；p0为入射脉冲的峰值功率。

1.2.1 群速度色散效应(GVD)产生的啁啾

现以高斯脉冲为例只考虑GVD效应对光脉冲传输的影响,式(10)变为

(11)

1) 无初始啁啾情况。考虑入射光场具有以下形式的高斯脉冲:

(12)

式中，T0为初始脉宽.

由式(11)和式(12)得:沿单模光纤传输到任一点z处的振幅为:

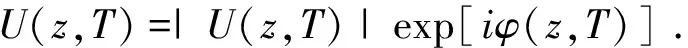
(13)

式中:

(14)

(15)

比较式(12)和式(13)可以看出,在GVD效应下,尽管入射高斯脉冲是不带啁啾的,即无相位调制,但经过光纤传输后变成了啁啾脉冲。同时由式(15)可知,脉冲的频率变化是线性的,即产生了线性的频率啁啾,啁啾δω(T)的正负和色散系数β2的符号有关。

图1 色散所致高斯脉冲的展宽Fig.1 Broadening of Gauss pulse induced GVD

对于高斯脉冲,无初始啁啾时,数值模拟了传输距离Z/LD=0,2,4时的|U(z,T)|2曲线如图1所示,可见对于一给定的色散长度LD,随着传输距离的增加,高斯脉冲在逐渐展宽,这是由于在色散效应GVD的影响下,不同频率分量的脉冲在光纤内的传输速度不尽相同,因此不同频谱分量在传输过程中的任何延迟都引起了高斯脉冲的逐渐展宽,模拟结果和理论的分析相吻合。

2) 源啁啾情况。对线性源啁啾高斯脉冲,其数学表达式为

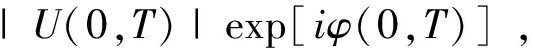
(16)

(17)

式中：c0为源啁啾参量;T0为初始脉冲宽度。

频率差即啁啾量为:

(18)

啁啾参量c为:

(19)

求解式(11)可得到传输距离z后,脉宽T1与初始脉宽T0的关系为:

(20)

式(20)表明,脉冲的宽度与GVD参量β2和啁啾的参量c0的相对符号有关,当β2c0为正时,高斯脉冲单调展宽;当β2c0为负值时,高斯脉冲有一个初始窄化的阶段。

图2是在GVD效应下,β2c0为正,且有初始啁啾时,数值模拟了高斯脉冲在光纤中传输的演变过程,传输距离取Z/LD=6,图2(b)是图2(a)的平面轮廓图,随着传输距离的增加,高斯脉冲在不断展宽,这点从图2(b)的分叉趋势就可以看出,同时发现在传播过程中,有初始啁啾的脉冲展宽比无初始啁啾的展宽趋势更明显,显然其作用还依赖于啁啾参量,这对于研究光纤通信的传输特性很有意义。可见,由于GVD的效应,带有初始啁啾的脉冲在光纤中的不同频率分量在传输的过程中同样有延迟的现象,从而导致脉冲的展宽,模拟结果与理论推导一致。

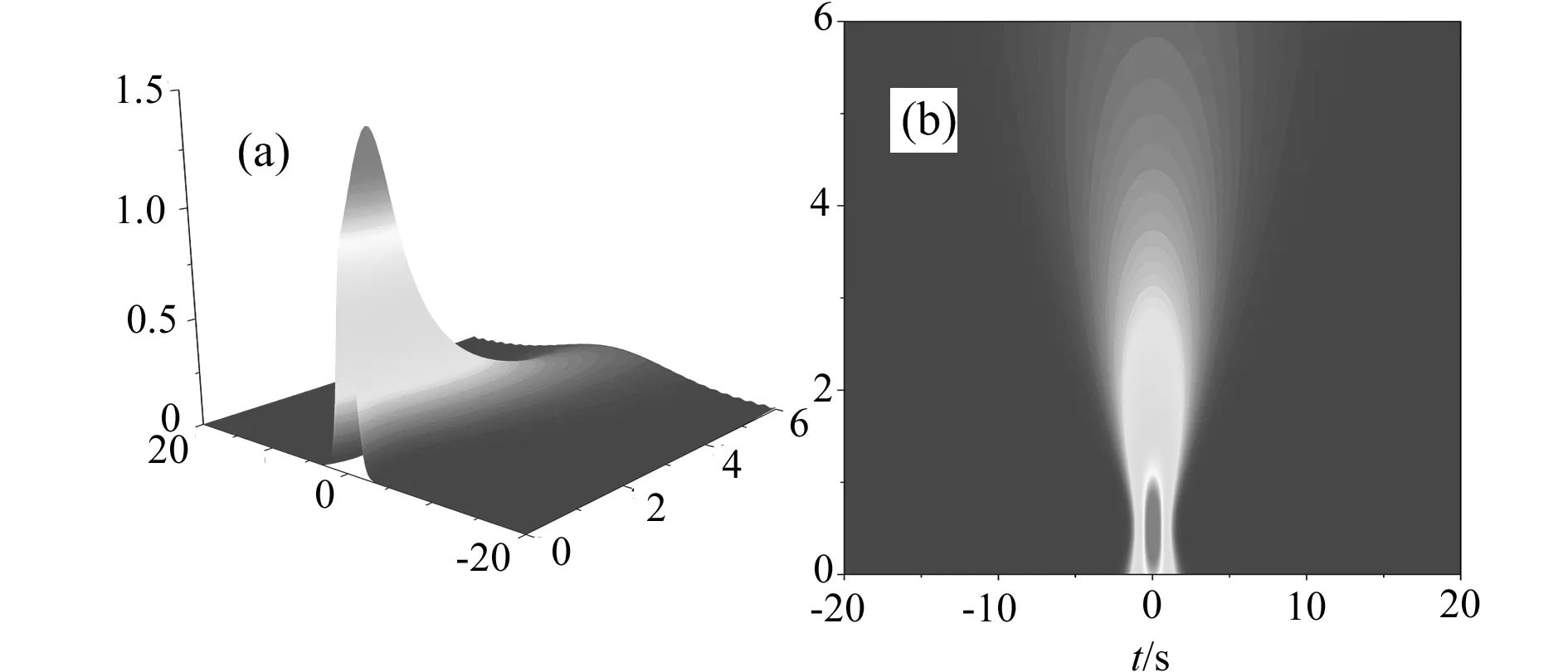
图2 色散所致高斯脉冲的演变Fig.2 Evolution of Gauss pulse induced GVD

1.2.2 自相位调制效应对啁啾特性的影响

1) 当c=0时。仅考虑自相位对高斯脉冲传播的影响,式(10)为

(21)

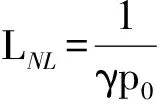
解式(21)得:

(22)

(23)

(24)

式(22)表明,SPM可以引起脉冲相位的变化,但脉冲形状保持不变,如图3所示仅在SPM效应下,数值模拟了高斯脉冲的演变图,图3(b)是图3(a)脉冲演化图的平面轮廓图,从其无分叉的现象就可说明脉冲形状的不变性;非线性相移φNL由式(23)给定,它随光纤长度zeff的增大而增大;由SPM引起的δω(T)与时间的关系可被看作频率啁啾,它随传播距离的增大而增大。

图3 自相位所致高斯脉冲的演变Fig.3 Evolution of Gauss pulse induced SPM

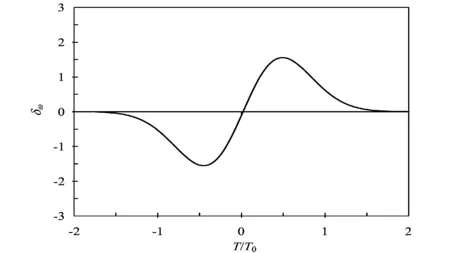
图4 由SPM感应的高斯频率啁啾Fig.4 Gauss frequency chirp induced SPM

如图4所示,假设光纤无损耗即α=0时,数值模拟得到了高斯脉冲在zeff=LNL处由于SPM的效应,引起的频率啁啾δω;图中给出了SPM所致频率啁啾δω与时间的依赖关系,可以看出δω在前沿附近是负的,而在后沿附近则变为正,并且在高斯脉冲中心附近较大范围内,啁啾是线性的且是正的,即随时间的增加,频率也在增大;究其原因是脉冲沿光纤传输时,新的频率分量在不断地产生,这些由SPM产生的频率分量展宽了频谱,使之超过了z=0处的初始宽度,同样导致了频率啁啾的产生。

2) 源啁啾情况。对给定源值式(16)解式(21)得到任一位置z处脉冲振幅、相位、频率啁啾分别为:

(25)

(26)

(27)

由此可见,SPM致脉冲产生的啁啾与初始啁啾有关,并且在传输的过程中,光脉冲的特性也会受到初始啁啾的影响。

1.2.3 GVD和SPM共同作用下的啁啾

同时考虑GVD和SPM时,由式(10)可求出频率啁啾的表达式为如下式(28):

(28)

可见,当LD和LNL一定时,δω是z和T的函数。而且,GVD和SPM同时作用于单模光纤传输脉冲时,会产生新的现象。在正常色散区域,GVD和SPM共同作用使光脉冲压缩;在反常色散区域,SPM所致啁啾为正,GVD所致啁啾为负;当LD=LNL时这两种啁啾作用在高斯脉冲的中心附近基本上相互抵消,在脉冲传播期间,使之尽可能平衡了这两种相反的啁啾,从而形成无啁啾稳定传输的脉冲——光孤子。

2 结论

研究表明GVD和SPM两者都产生相应的啁啾,但产生机理不同。GVD所致啁啾是把光脉冲中不同频率分量重新分布,产生线性啁啾,不产生新的频率光子;而SPM所致啁啾是产生了新的频率分量引所致的啁啾。GVD和SPM产生的啁啾相互作用达到平衡时,可实现无啁啾脉冲稳定传输的光孤子, 这对于脉冲传播特性和光通信的研究非常有意义。

[1] 段巍,杨茂磷,葛勇.高斯脉冲在单模光纤中的传输特性分析[J].太原理工大学学报,2006,37(4):476-479.

[2] 贾东方,余震虹,等.非线性光纤光学原理及应用[M].北京:电子工业出版社,2010.

[3] 石顺祥,陈国夫，等.非线性光学[M].西安:电子科技大学出版社,2002.

[4] 赵环.啁啾脉冲激光放大系统中的色散研究[J].宇航计测技术,2013,33(1):23-30.

[5] 宋秀玲.群速度色散对双曲正弦高斯脉冲传输的影响[J].重庆三峡学院学报,2012,28(139):46-50.

[6] 孙美智,康俊,郭爱林,等.单模光纤对啁啾脉冲对比度的影响[J].光学学报,2010,30(5):1234-1237.

[7] 朱莉娟.自相位调制的频谱展宽研究[J].光通信研究,2009,155(5):30-32.

[8] PARK K J,YOUN C J,LEE J H,et al.Effect of self-phase modulation on group-velocity dispersion measurement technique using PM-AM conversion[J].2002,38(21):1247-1248.

[9] HUANG Yuru,CHIU Peichin,CHYI Jeninn,et al.A study on the fiber dispersion effect for the generation of quasi-sinusoidal terahertz modulations on optical pulses[J].2015,33(23):4899-4907.

[10] LEE H,AGRAWAL G P.Impact of self-phase modulation on instabilities in fiber lasers[J].Quantum Electronics,2010,46(12):1732-1738.

[11] 董毅,赵尚弘,李勇军,等.半导体光放大器中SPM效应对光脉冲传输性能的影响[J]. 红外与激光工程,2014,43(5):1411-1415.

[12] 田小程,隋展,黄志华,等.直接相位调制产生周期性线性啁啾脉冲特性研究[J].物理学报,2013,62(10):104216(1-9).

(编辑：刘笑达)

Chirp and Influence of SPM and GVD in Single-mode Fiber

FAN Linlina，QIAO Jipingb

(Taiyuan University of Technology,a.College of Physics and Optoelectronics,b.CollegeofElectricalandPowerEngineering,Taiyuan030600,China)

The concept of frequency chirp was summarized by theoretical deduction,and on the basis of the nonlinear Schrödinger Equation, the generation of chirp with the influence of group velocity dispersion (GVD) and self phase modulation (SPM) and its effect on the pulse propagation were studied by numerical simulation. The results show that the different generation mechanisms of chirp can be obtained by two kinds of effects of GVD and SPM. The results are important for the study of optical pulse transmission characteristics in optical fibers.

frequency chirp;group velocity dispersion;self phase modulation;optical soliton

1007-9432(2016)05-0669-04

2016-02-26

山西省科技厅青年基金项目(2014021011-1);国家自然科学青年基金项目(NO.11205112)

樊林林(1979-),女,山西太原人,工程师,主要从事激光非线性特性方面的研究,(E-mail)fll800@126.com

TN929.11

A

10.16355/j.cnki.issn1007-9432tyut.2016.05.020