基于强度参数演化的胶凝砂砾石材料本构关系研究
李秀文,彭云枫,王万顺
(1.中国水利水电科学研究院,北京 100038; 2.三峡大学 水利与环境学院,湖北 宜昌 443002)
基于强度参数演化的胶凝砂砾石材料本构关系研究
李秀文1,彭云枫2,王万顺1
(1.中国水利水电科学研究院,北京 100038; 2.三峡大学 水利与环境学院,湖北 宜昌 443002)
胶凝砂砾石材料应力-应变关系具有明显的弹塑性和应变软化特性,当前其本构关系推导较为复杂。针对这一问题,本文借鉴岩石材料峰后强度参数演化行为,基于摩尔-库伦强度准则,采用最大主应变ε1作为应变软化参数,将凝聚力c、内摩擦角φ看作ε1的分段线性函数,较为简便的推导胶凝砂砾石材料的本构关系。由本构关系式拟合得到不同围压时胶凝砂砾石材料应力-应变关系曲线变化趋势与三轴试验数据吻合良好,说明该方法得到的本构关系可以反映胶凝砂砾石材料的应力-应变特征。
胶凝砂砾石材料;强度参数演化;三轴试验;本构关系
1 研究背景
胶凝砂砾石材料是一种复杂新型材料,其力学特性受胶凝材料用量、围压、含砂率、水灰比及骨料级配等许多因素影响,材料具有明显的非线性特征[1]。胶凝砂砾石材料在峰后变形阶段,轴向应变增大而偏差应力逐渐减小,表现出应变软化特征,其力学行为比较复杂,较难用经典的强度理论进行研究。
在胶凝砂砾石材料本构关系研究方面,一些专家从不同角度做了大量的工作。孙明权等[2]采用“虚加刚性弹簧法”和“分布迭代法”解决了胶凝砂砾石材料特性引起的负刚度问题。吴梦喜等[3]提出由堆石元件和胶结元件构成的胶凝砂砾石材料二元并联模型,可描述胶凝砂砾石材料应力-应变非线性特征又能描述变形模量随龄期增长的特征。何蕴龙等[4]根据Hardfill材料的应力-应变关系特点,研究确立了胶凝砂砾石材料的本构模型,由三轴试验数据得出峰值应力差、残余强度、峰值应变及初始弹性模量与围压的关系,进而方便的确定全部模型参数。A Batmaz等[5]人在设计Cindere坝时,采用分段线性有限元的方法,通过分段采用修正牛顿迭代法近似的模拟胶凝砂砾石材料非线性应力-应变关系,取得较好效果。
本文借鉴研究岩石材料峰后力学行为方面的方法,基于摩尔-库仑(Mohr-Coulomb)强度准则,采用最大主应变ε1作为应变软化参数,凝聚力c、内摩擦角φ看作ε1的分段线性函数,给出了胶凝砂砾石材料本构关系具体求法。该方法简单易行,能揭示胶凝砂砾石材料应变软化的机制,便于与工程实践相结合。算例结果表明,该方法对于研究胶凝砂砾石应力-应变关系是有效的。
2 强度参数演化规律和本构关系的求法
2.1 胶凝砂砾石材料应力-应变关系及研究思路 在不同围压作用下,胶凝砂砾石材料的应力-应变关系可以分为近似直线阶段、曲线上升阶段和曲线下降阶段,其破坏强度满足摩尔-库伦强度准则[3,6]。Hoek等[7]根据GSI的取值不同提出了岩石3种不同的峰后变形模式,分别是理想弹塑性模型、理想弹脆塑性模型和应变软化模型,如图1所示。
采用理想弹脆塑性模型和应变软化模型来研究峰后的力学行为时,除需要确定峰值处的力学参数,还需要确定残余阶段的力学参数及峰后软化阶段力学参数的演化规律。虽然一些专家学者从强度参数的演化行为角度开展了峰后变形的研究,但总体上模型逐渐趋于复杂,不便于工程应用。以最大主应变ε1作为应变软化参数,基于强度参数与应变软化参数ε1的关系研究峰后应力-应变关系的研究较少[8]。
本文推导胶凝砂砾石材料本构关系的基本思路和方法为:(1)确定强度准则,通过强度准则建立应力和强度参数之间的关系;(2)确定强度参数的演化规律,由强度参数的演化规律可以建立强度参数与应变软化参数之间的联系;(3)采用强度参数这一中间变量得到应力-应变软化参数的关系,从而得到胶凝砂砾石材料的本构关系。
2.2 强度准则 比较常用的研究岩石材料强度准则有摩尔-库仑强度准则和Hoek-Brown强度准则等,摩尔-库仑强度准则表达式为:

Hoek-Brown强度准则表达式为:

式中:γ为应变软化参数;c、φ、σc、m、s、a为强度参数,在峰后应变软化阶段,这些强度参数会随应变软化参数γ的变化而变化,本文计算将采用摩尔-库仑强度准则。
2.3 软化参数 选择应变软化参数γ时,通常有两种不同做法:
(1)将γ视为内变量函数,比较常用的有

(2)基于增量的方法选取,比较常用的有

2.4 强度参数演化规律和本构关系的求法 一般可以通过试验、数值模拟等方法来获取强度参数与应变软化参数之间的关系,即强度参数的演化规律;为了便于问题简化,通常会假设强度参数与应变软化参数之间为分段线性函数的关系[9],表达式为:

式中:ξ为强度参数、ξp为峰值处的强度参数、ξr为残余阶段的强度参数值;γ*为应变软化参数γ在残余阶段开始处的值。对应的曲线如图2所示。
胶凝砂砾石材料本构关系推导采用摩尔-库仑准则作为强度准则,主应变ε1作为应变软化参数,故需要确定凝聚力c、内摩擦角φ和ε1之间的关系;图3为胶凝砂砾石材料全应力-应变关系曲线[10],由图3可以得出,在达到弹性强度之前,应力-应变成直线关系;在弹性强度和极限强度之间,应力-应变关系曲线斜率发生变化。结合前人的做法,并与胶凝砂砾石材料全应力-应变曲线对应起来,假设材料强度参数c、φ的演化规律如式(7)、式(8)所示,对应的演化曲线如图4所示。

图1 岩石材料峰后变形的3种模式
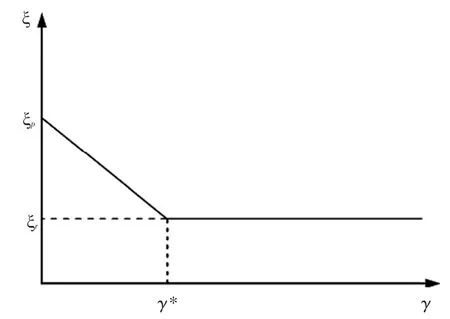
图2 强度参数的演化曲线

图3 胶凝砂砾石材料全应力-应变曲线

图4 强度参数c、φ的演化曲线

式中:εt、εp、εr分别为弹性强度、峰值强度和残余强度开始处的主应变。
将式(7)、式(8)带入式(1),即可求出胶凝砂砾石材料的本构关系。公式如下:

3 Excel规划求解三轴试验抗剪强度指标
基于孙明权教授C50胶凝材料三轴试验[10]结果,本文采用非线性规划方法,模拟三轴试验的强度包线,建立了由目标函数和约束条件方程组构成的数学模型,并利用Excel对其进行求解和绘图,从而实现了试验数据的自动处理并可自动绘图。
采用Excel规划求解首先设计一个工作表,由已建立的数学模型,将决策变量、约束条件、目标函数等依次排列,并在工作表中将相关固定信息初始化[11],人工绘图计算与用本程序计算结果误差,凝聚力绝对差为0.2~0.4 kPa,内摩擦角绝对差为0.2°~0.5°。峰值强度计算结果见表1。

表1 规划求解计算结果
胶凝砂砾石材料峰值强度时摩尔-库伦绘图效果见图5。

图5 三轴试验极限应力圆及强度线
4 算例
为了验证该本构关系的合理性,根据文献[10]数据并进行整理,采用Excel规划求解三轴试验抗剪强度指标,分别将弹性强度、峰值强度、残余强度基于摩尔-库伦准则计算出其对应的凝聚力c和内摩擦角φ,得到结果见表2。
以围压σ3=200 kPa为例,说明本构关系的具体求法。首先把σ3=200 kPa时对应的参数ct、cp、cr、φt、φp、φr、εt、εp、εr分别带入式(7),式(8),可求得凝聚力和内摩擦角的演化规律,其中c、φ的演化规律分别如式(10)、式(11)所示。

表2 三轴试验数据

将式(10)、式(11)带入摩尔-库伦强度准则的表达式(1),即可得到σ3=200 kPa时的本构关系式。由于关系式过于冗长,此处不再列出,对应的应力-应变曲线如图6所示。

图6 胶凝砂砾石材料应力-应变拟合曲线
同理,可以求出在其余围压下的应力-应变曲线,为了验证本构模型的合理性,将三轴试验数据在图中用点标示出来,见图7。

图7 不同围压下应力-应变数值模拟曲线与试验数据对比
从图7可以得出,不同围压时数值拟合曲线变化趋势与三轴试验测得的数据变化趋势吻合良好,表明使用本文所提出的方法推导胶凝砂砾石材料的本构关系是合理的。
5 结论
(1)本文基于强度参数的演化行为,提出了胶凝砂砾石材料建立本构关系的一般方法,基于该材料的应变特征,做了相应改进。首先确定强度准则和应变软化参数,然后根据三轴试验结果,找出强度准则中的强度参数与应变软化参数之间的关系,最后以强度参数作为中间变量,将应力与应变联系起来,从而得到胶凝砂砾石材料本构关系。(2)基于摩尔-库仑强度准则,以最大主应变ε1作为应变软化参数,将凝聚力c,内摩擦角φ视为ε1的分段线性函数,给出了本构关系式的具体求法。利用本文本构关系拟合得到不同围压下胶凝砂砾石材料应力-应变曲线,并与三轴试验数据进行了对比,结果表明,数值拟合曲线的变化趋势与试验数据基本一致,说明利用本文的方法进行研究是合理的。并且该方法简便易行,便于实现与工程结合。
[1] 孙明权,杨世锋,张镜剑.超贫胶结材料本构模型[J].水利水电科技进展,2007,27(3):35-37.
[2] 孙明权,彭成山,陈建华,等.超贫胶结材料坝非线性分析[J].水利水电科技进展,2007,27(4):42-45.
[3] 吴梦喜,杜斌,姚元成,等 .筑坝硬填料三轴试验及本构模型研究[J].岩土力学,2011,32(8):2241-2249.
[4] 何蕴龙,刘俊林,李建成.Hard fill筑坝材料应力-应变特性与本构模型研究[J].四川大学学报:工程科学版,2011,43(6):40-47.
[5] Balkema A A,Rotterdam.Cindere dam-107m high roller compacted Hardfill dam(RCHD)in Turkey[C]//Proceedings 4th International Symposium on Roller Compacted Concrete Dams.Madrid,2003:121-126.
[6] 柴启辉.胶凝砂砾石坝材料力学性能试验及施工工艺初步探讨[D].郑州:华北水利水电学院,2012.
[7] Hoek E,Brown E T.Practical estimates of rock mass strength[J].International Journal of Rock Mechanics and M ining Sciences,1997,34(8):1165-1186.
[8] 韩建新,李术才,李树忱,等.基于强度参数演化行为的岩石峰后应力-应变关系研究[J].岩土力学,2013,(2):342-346.
[9] Lee Y K,Pietruszczak S.A new numerical procedure for elasto-plastic analysis of a circular opening excavated in a strain-softening rockmass[J].Tunnelling and Underground Space Technology,2008,23:588-599.
[10] 孙明权,彭成山,李永乐,等.超贫胶结材料三轴试验[J].水利水电科技进展,2007,27(4):46-49.
[11] 阮波,张向京,彭意 .Excel规划求解三轴试验抗剪强度指标[J].铁道科学与工程学报,2009,6(5):57-60.
Study on the constitutive relation of cemented sand and gravel material
based on strength parameter evolution
LI Xiuwen1,PENG Yunfeng2,WANG Wanshun1
(1.China Institute of Water Resource and Hydropower Research,Beijing 100038,China;2.College of Hydraulic&Environmental Engineering,China Three Gorges University,Yichang 443002,China)
The stress-strain relationship of the cemented sand and gravel material has the characteristics of elastic-plastic and strain softening,and its constitutive relationship derivation is relatively complicated. Therefore,a method for deducing the constitutive relationship of the cemented sand and gravel material is presented.By using the evolution of post-peak strength parameters of rock material for reference,and regarding maximum principal strainε1as strain softening parameter and the cohesion c and friction angleφ as the piecewise linear functions ofε1,the constitutive relationship of cemented sand and gravel material is deduced based on Mohr-Coulomb strength criterion.The stress-strain curves under different confining pressures are obtained through constitutive relationship fitting and agree well with the triaxial test data.It reveals that the constitutive relationship obtained through this method may reflect the characteristic of stress-strain of cemented sand and gravel material.
cemented sand and gravel material;strength parameter evolution;triaxial test;constitutive relationship
TV64
A
10.13244/j.cnki.jiwhr.2016.03.002
1672-3031(2016)03-0171-06
(责任编辑:李 琳)
2015-11-19
湖北省自然科学基金项目(2014CFB235)
李秀文(1987-),男,山东临沂人,硕士,助理工程师,主要从事工程安全监测研究。E-mail:lixw912@163.com

