振动信号基频测量发动机转速
马 燕,聂晓会,王丽惠,刘丽伟
(长春工业大学 计算机科学与工程学院,吉林 长春 130012)
振动信号基频测量发动机转速
马 燕,聂晓会,王丽惠,刘丽伟*
(长春工业大学 计算机科学与工程学院,吉林 长春 130012)
分析了振动信号基频与转速之间的关系,将小波分析、三相关分析、傅里叶变换、CZT变换结合提取基频。MATLAB仿真分析得出提取的基频相对误差在0.8% 以内,实车试验证明了新算法能快速准确地测量出转速且误差很小。
基频;转速;小波;傅里叶变换;仿真分析
0 引 言
在发动机的故障诊断中,发动机的转速是分析估计发动机性能的一个重要参数,一些传统的测量转速的方法会在测量过程中带来不便,而发动机的振动信号包含了丰富的信息且振动信号的基频与转速之间具有一定的关系[1],对振动信号的采集也越来越快速方便,故通过振动信号测量转速的方法已经在一定程度上取代了传统的测量方法。
发动机工作时振动信号的频率与曲轴转速具有一定的数学关系[2],即
(1)
式中:n——发动机转速;
f0——振动信号基频;
τ——气缸个数;
i——发动机冲程数。
发动机转速测量问题的关键在于提取振动信号的基频。而发动机的原始振动信号是由一系列的以主轴转动频率为基频的谐波组成,变化复杂,是一种非平稳的时变信号[3]。一般情况下,通过传感器采集到的振动信号都带有噪声,所以要先进行有效去噪,才能进一步对振动信号进行处理。
1 小波阈值去噪
信号去噪是信号处理领域的经典问题之一,传统的去噪方法主要包括线性滤波方法和非线性滤波方法,如中值滤波和Wiener滤波等[3]。传统去噪方法的不足在于使信号变换后的熵增高,无法刻画信号的非平稳特性,并且无法得到信号的相关性[4]。为了克服上述缺点,可以用小波变换解决信号去噪问题。
小波变换具有下列比较好的特性[5]:
1)低熵性。小波系数的稀疏分布使信号变换后的熵降低。
2)多分辨率性。可以非常好地刻画信号的非平稳性,如边缘、尖峰、断点等。
3)去相关性。可以取出信号的相关性,且噪声在小波变换后有白化趋势,所以比时域更利于去噪。
4)选基灵活性。由于小波变换可以灵活选择基函数,因此可根据信号特点和去噪要求选择合适小波。
一般来说,小波阈值去噪的基本思路是:选择合适的小波基和分解层数将振动信号分解,对分解的高频系数选择合适的阈值进行量化,最后使用小波分解的低频系数以及阈值量化处理后的高频系数进行小波重构即可[6]。从上述的过程来看,对高频系数进行量化的阈值选取尤为重要,阈值过高和过低都会对去噪过程带来影响,甚至达不到去噪的目的。MATLAB自带的含噪声的电网信号[7]如图1所示。
对该信号进行去噪,选用sym5小波基将leleccum信号分解到第5层,对各层噪声分别进行估计、调整,用minimaxi阈值选择对系数进行软阈值处理,消除噪声。可见,小波阈值去噪的应用非常广泛灵活,且去噪效果明显[3]。
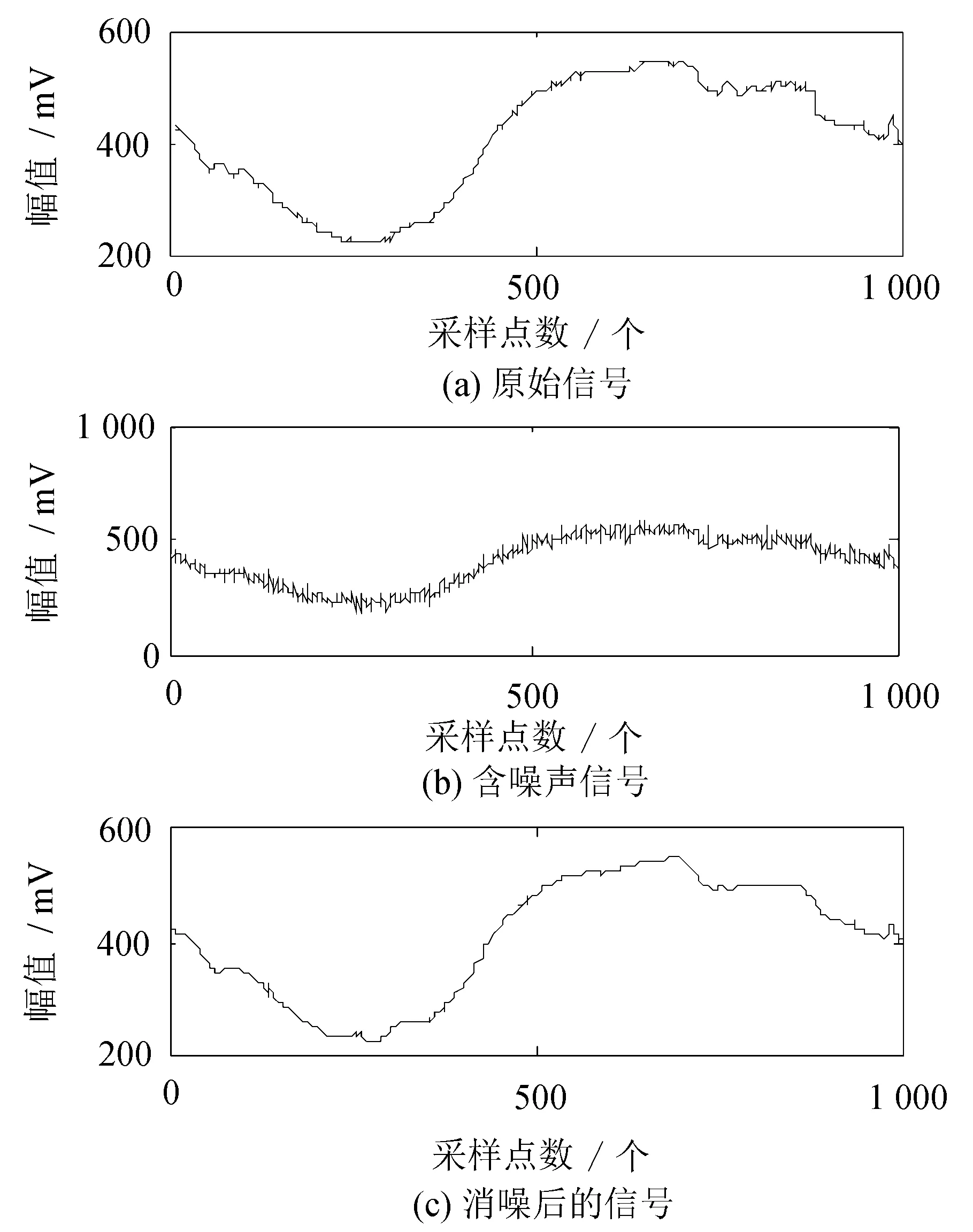
图1 小波对leleccum信号的去噪
2 三相关分析
相关分析是随机信号在时域上的统计分析,可以检测混淆于随机过程中的周期信号,并根据相关函数的宽窄来判断信号频率成分丰富与否,描述随机信号过程相关性时延的变化情况[8]。
根据振动信号形成机理可知,它的激励源具有周期性,但振动信号的变换非常复杂,并不是标准的周期信号,在理想情况下,也只是准周期信号。如果对含有噪声的周期信号做自相关处理,在强噪声背景下,微弱的周期信号很难明显表现出来,但对振动信号作多重相关分析,不仅能有效地抑制噪声部分,而且还能不断地突显信号的周期信息。相关次数越多,相关运算结果越准确,信噪比越高,在强噪声背景下检测到微弱的周期性信号的机会越大。
自相关分析是对同一随机振动样本函数随时间坐标移动进行相似程度计算,三重相关是在一次自相关函数结果的基础上,再进行3次自相关运算。设实际信号为
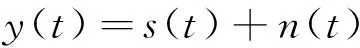
其中,s(t)为有用信号,n(t)为噪声信号,则y(t)的自相关函数的运算结果为:
(2)
(3)
式中:n1(t)——一次自相关后余下的残留噪声。
三相关函数的运算结果为:
(4)
分析结果表明,三相关后的噪声已经明显很小了,故用三相关分析就能达到很好的效果。频率为30 Hz的加噪正弦信号及其自相关分析分别如图2和图3所示。
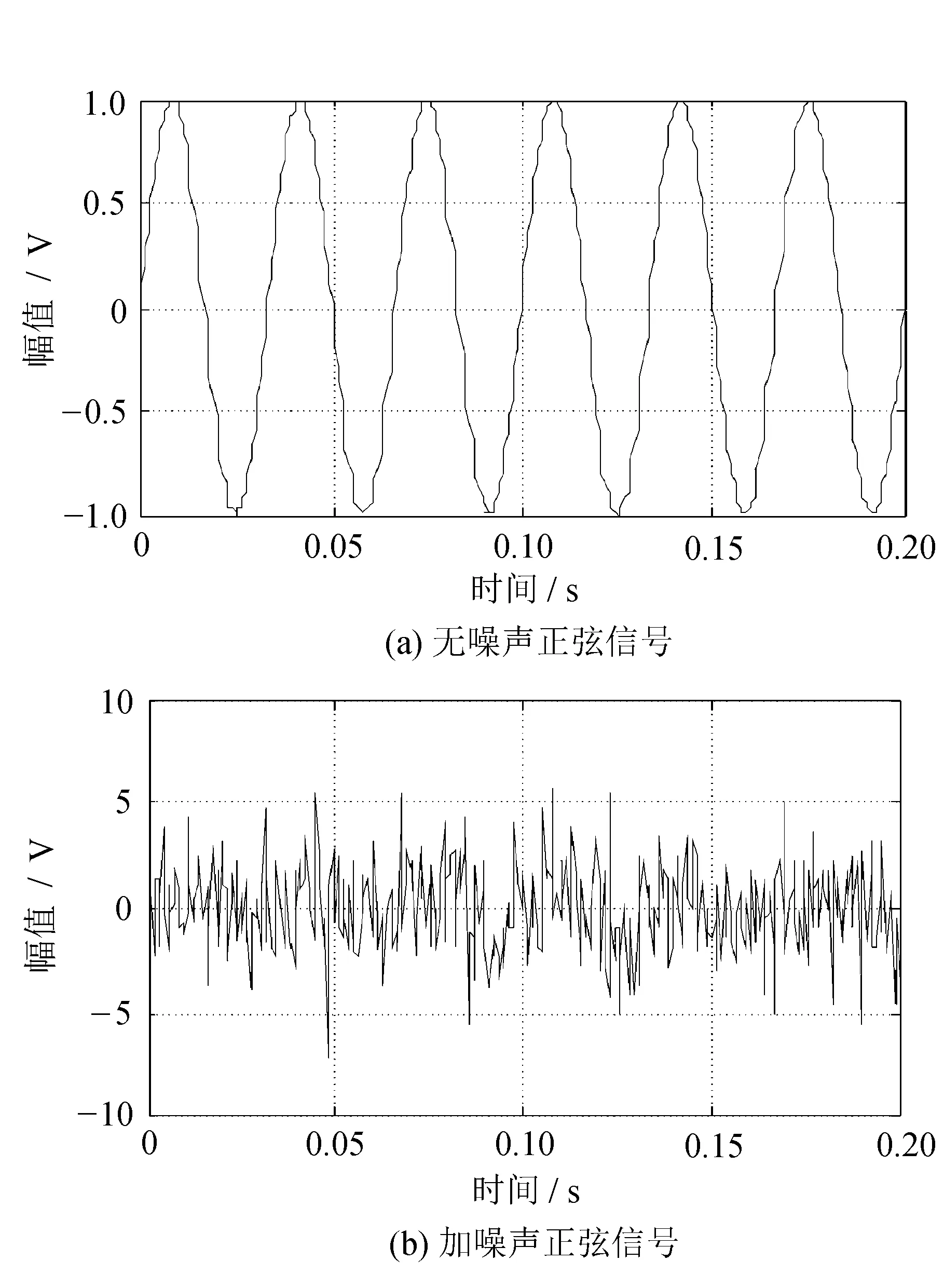
图2 被随机噪声污染的正弦信号
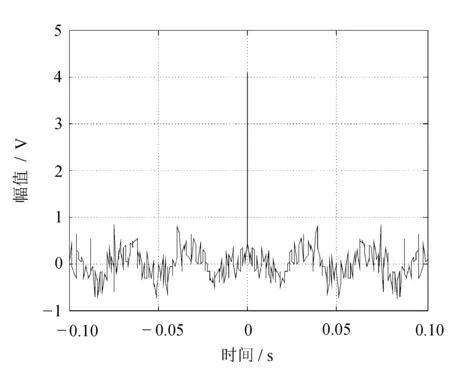
图3 加噪正弦信号的自相关分析
三相关分析结果如图4所示。
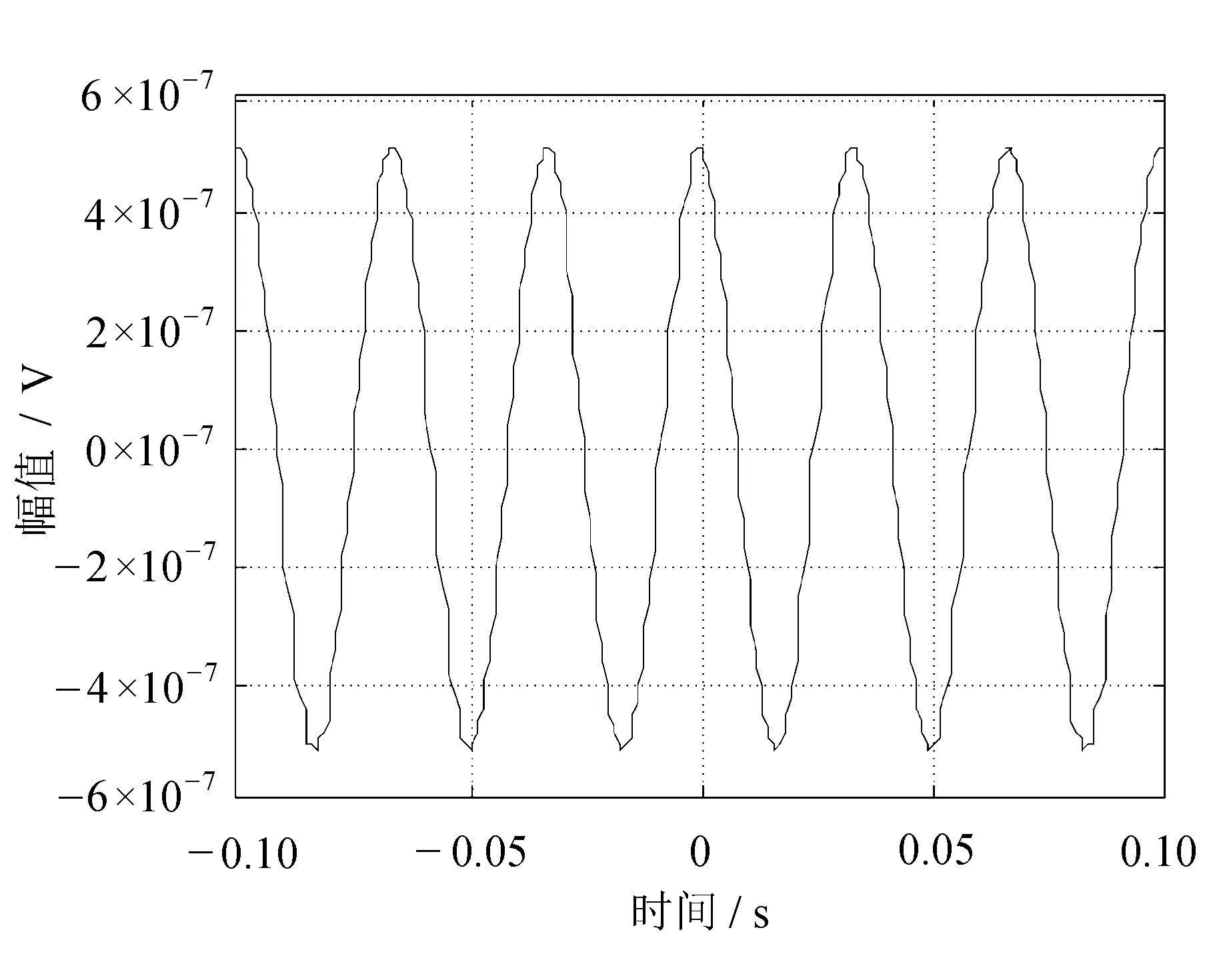
图4 正弦加噪声信号的三相关分析
三相关分析相比自相关分析更能取得较好的去噪效果,得到信号的边缘更平整,在后面的包含谐波的振动信号分析中也能得出其突显信号周期的作用。
3 CZT分析
ChripZ变换是一种更为灵活的计算频谱的算法,可以用来计算单位圆上任一段曲线的Z变换,它可以只分析信号所在的一段频带,此频带之外的部分不考虑,是螺旋线上的采样,可以通过FFT实现,并且可以更清楚地分析局部频率,对分析振动信号的局部频谱分析来说,同时也减少了运算量。
给定一个离散信号x(n),它的单边Z变换为:
(5)
令zr= AW-r,其中
(6)
(7)
(8)
A0为W0任意的正实数,给定A0,W0,θ0,ω0,当r从零到无穷大时,可得到在Z平面上的一系列点z0,z1,…,z∞,取这些点的Z变换,有:
(9)
这便是ChirpZ变换的定义[1]。图2中正弦加噪声信号三相关的FFT和CZT分析结果分别如图5和图6所示。
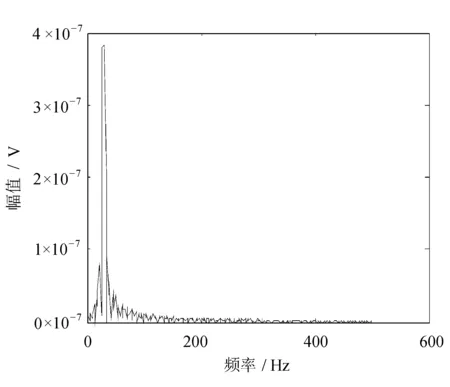
图5 加噪正弦信号FFT分析
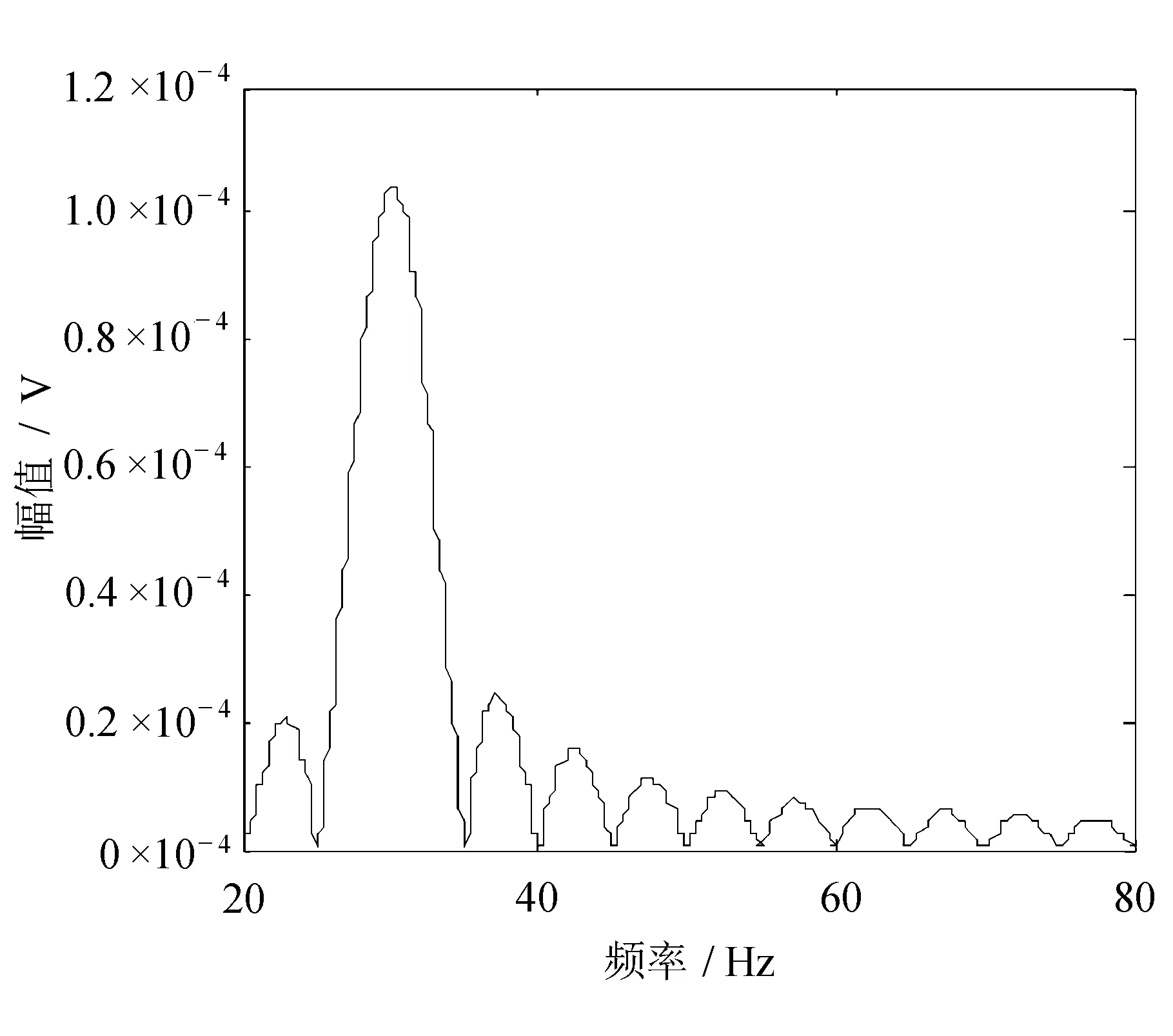
图6 加噪正弦信号CZT分析
可见利用CZT只对所需的频带进行分析,具有更高的频率分辨率。
4 提取基频改进算法
改进算法有如下4个步骤:
1)小波去噪。选择合适的小波和阈值对振动信号进行分解和重构,达到去噪的目的。
2)相关分析。对去噪后的信号进行三相关分析。
3)FFT分析。对去噪后的三相关函数进行傅里叶变换,确定所需的频带范围。
4)CZT分析。在所需的频带对三相关函数进行ChripZ变换。
基频为50 Hz并包含多次谐波且被噪声污染的振动仿真信号及其去噪后的结果如图7所示。
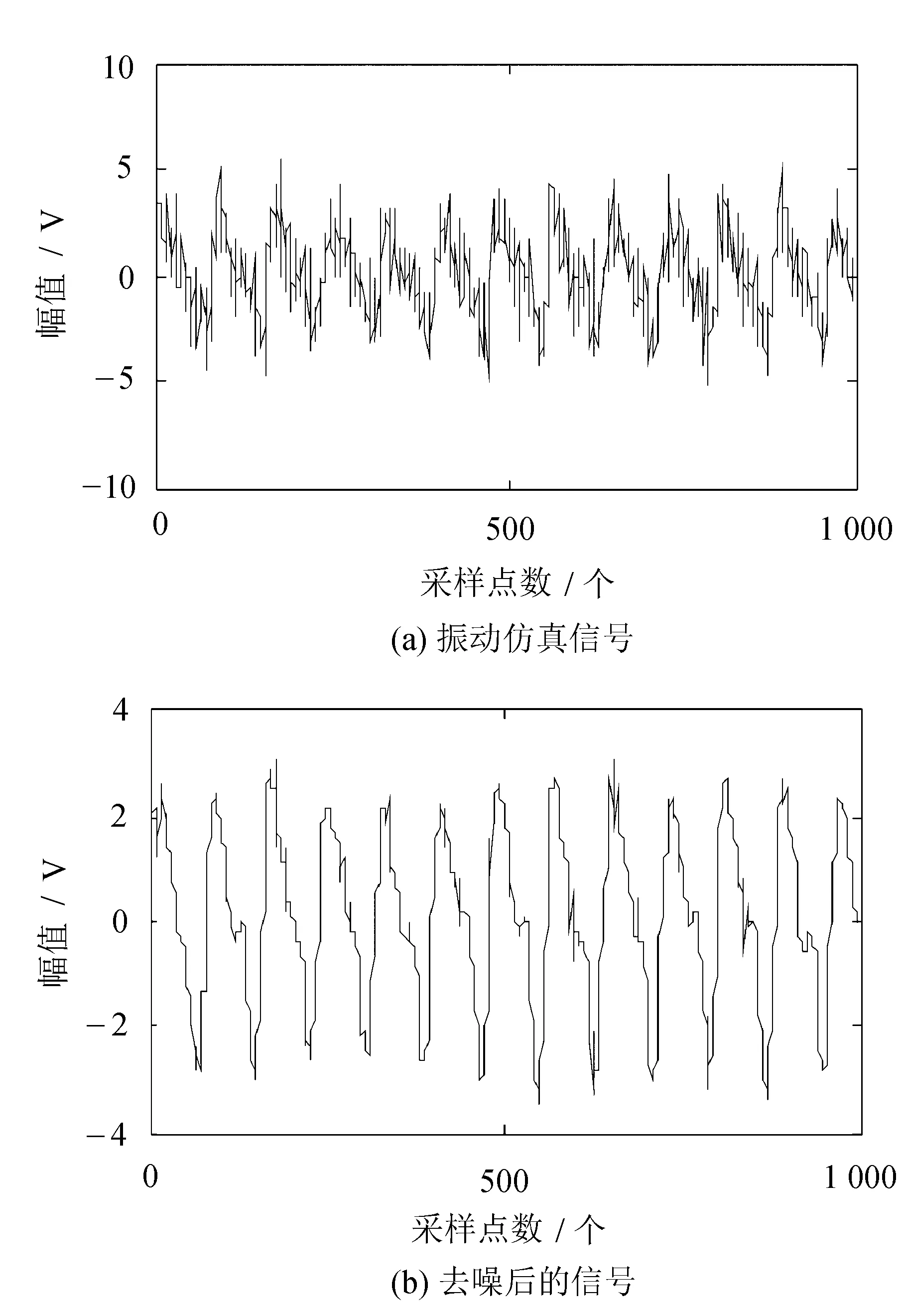
图7 振动信号仿真与去噪
选用小波基db9将信号进行四层分解,对各层噪声分别进行估计、调整,用rigrsure阈值选择对系数进行软阈值处理。振动仿真信号的自相关和三相关分析如图8所示。
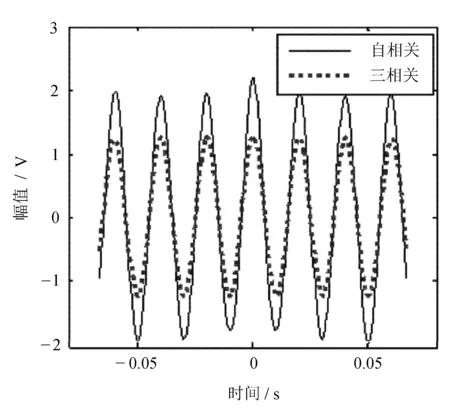
图8 自相关和三相关分析
可见三相关逐渐突显出振动信号的周期性。
三相关函数的FFT结果和三相关函数的CZT变换分别如图9和图10所示。
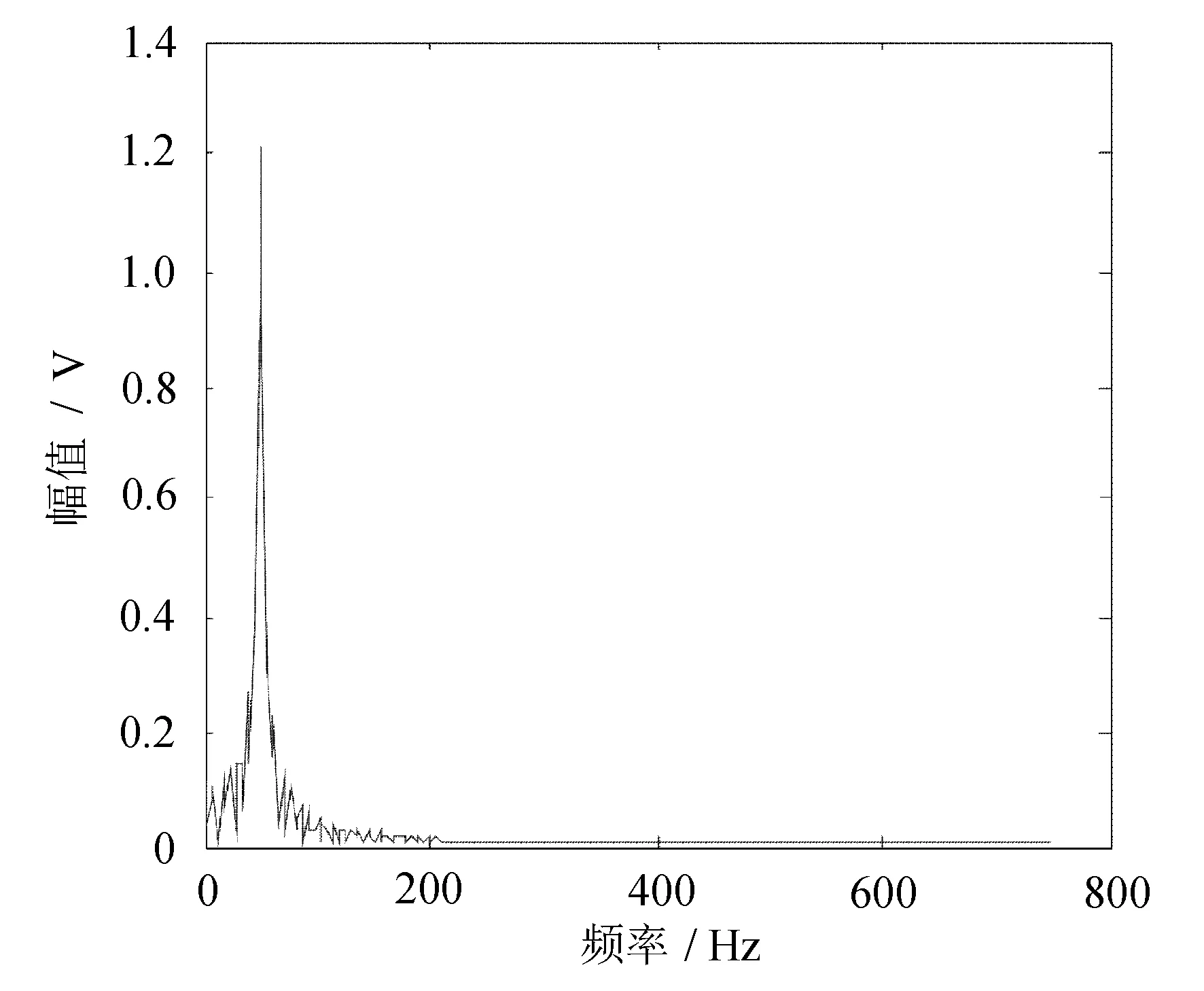
图9 振动信号FFT分析
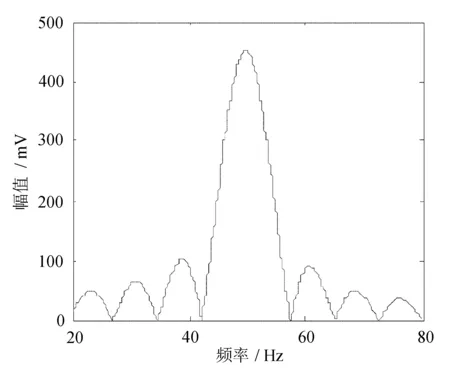
图10 振动信号CZT分析
由分析结果可知,新算法提取的基频为49.6 Hz,相对误差为0.8%,误差很小,从而使转速精确度大大提高。
5 实车试验
以起亚狮跑2.0轿车四缸四冲程发动机作为试验对象,采用武汉四方光电科技公司的压电式振动传感器进行发动机振动信号采集,如图11所示。

图11 发动机表面振动信号采集
车子空转到800、1 200、2 000 r/min的情况下采集到的振动信号分别如图12~图14所示。
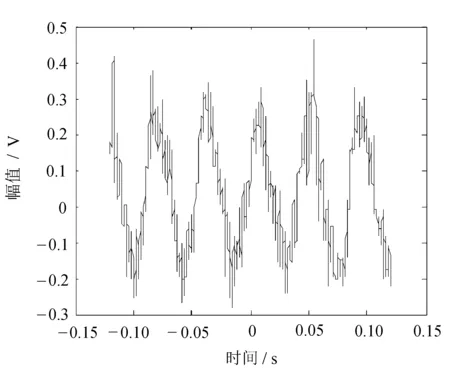
图12 800 r/min时振动信号
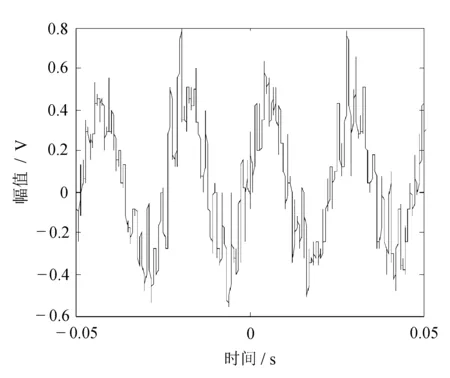
图13 1 200 r/min时振动信号
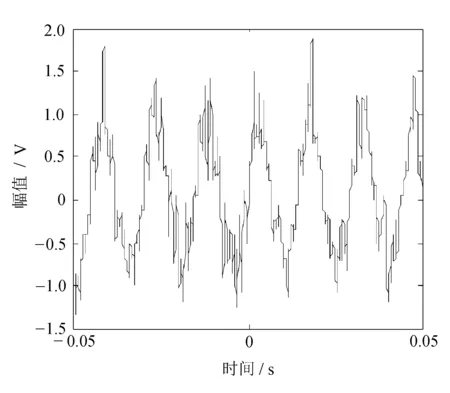
图14 2 000 r/min时振动信号
在上述3种转速情况下利用新算法提取基频的结果,最大幅值所对应的频率点分别为26.4、39.7、66.2 Hz。3种转速下的CZT分析如图15所示。
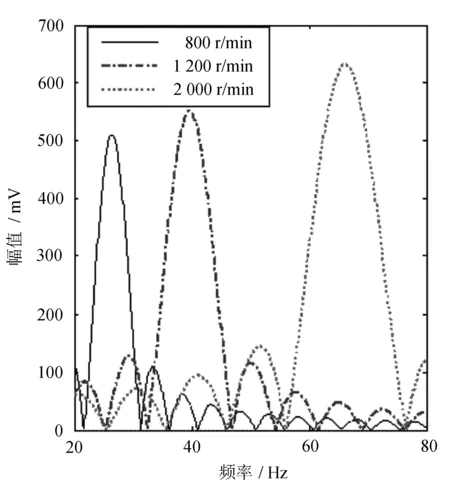
图15 3种转速下的CZT分析
通过式(1)得出转速,并与实际转速进行比较,结果见表1。
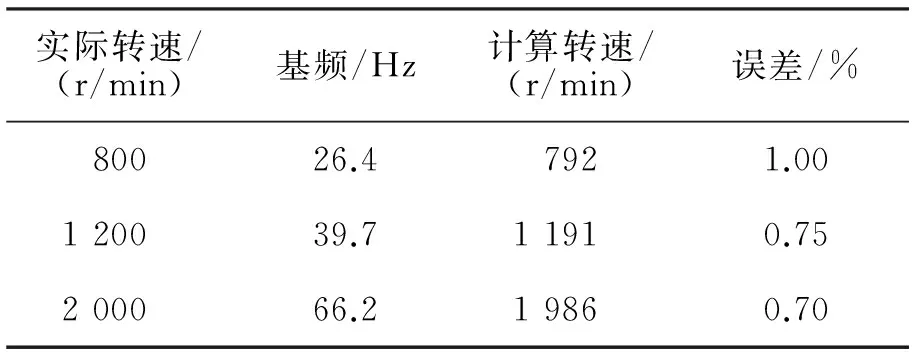
表1 测量转速与实际转速对比
6 结 语
从以上仿真结果和实验验证结果可以看出,文中提出的将小波去噪、多相关分析、傅里叶变换和CZT变换融合在一起的新算法能很好地提取发动机振动信号的基频,且精确度很高,从而使发动机的转速测量更快速准确。其基本思想在于结合四种方法的优点用于同一振动信号基频的提取,难点是小波去噪过程中小波基和阈值的选择。而且新算法也十分适合对振动信号的分析,有利于后续对振动信号的研究和发动机性能的测试。
[1] Song Xiang,Li Xu,Zhang Weigong. The new measurement Algorithm of the engine speed base on the basic frequency of vibration signal [C]//CMCE2010.Changchun,China:[s.n.],2010.
[2] 吕平,薛知行,张学敏,等.基于振动的内燃机转速测量研究[J].车辆与动力技术,2005(4):22-25.
[3] Zou L H,Liu A P,Ma X,et al. Synthesis of vibration waves based on wavelet technology [J]. Shock and Vibration,2012,19(3):391-403.
[4] 田彦,李奇涵,汤海涛.小波分析在滚动轴承故障诊断中的应用[J].长春工业大学学报:自然科学版,2011,32(6):595-600.
[5] 张德丰.详解MATLAB数字信号处理[M].北京:电子工业出版社,2010.
[6] Han M,Lin Y H,Xi J H,et al. Noise smoothing for nonlinear time series using wavelet soft threshold [J]. IEEE Signal Processing Letter,2007,14(1):62-65.
[7] 薛年喜.MATLAB在数字信号处理中的应用[M].北京:清华大学出版社,2008.
[8] 左泽敏,李舜酩,郑娟丽.相关分析在机械振动信号处理中的应用[J].机械制造与研究,2009,38(1):75-79.
Engine speed measurement based on vibration signal fundamental frequency
MA Yan,NIE Xiaohui,WANG Lihui,LIU Liwei*
(School of Computer Science and Engineering,Changchun University of Technology,Changchun 130012,China)
Relationship between the fundamental frequency of vibration signal and speed is analyzed first,and then wavelet analysis,three correlation analysis,Fourier transformation and CZT transform are combined to extract the fundamental frequency. MATLAB based simulation shows that the relative error of fundamental frequency extraction is less than 0.8%. The vehicle tests verify that the algorithm can measure speed in short time with low error.
fundamental frequency; speed; wavelet; Fourier transformation; simulation analysis.
2016-01-25
吉林省科技发展计划基金资助项目(20140441008SC)
马 燕(1988-),女,汉族,安徽桐城人,长春工业大学硕士研究生,主要从事嵌入式系统方向研究,E-mail:931710728@qq.com. *通讯作者:刘丽伟(1974-),女,汉族,吉林通化人,长春工业大学副教授,博士,主要从事模式识别和智能系统方向研究,E-mail:liuliwei@ccut.edu.cn.
10.15923/j.cnki.cn22-1382/t.2016.5.13
TP 391.9
A
1674-1374(2016)05-0479-06

