A Unification of the Concepts of the Variational Iteration,Adomian Decomposition and Picard Iteration Methods;and a Local Variational Iteration Method

Xuechuan Wang,Satya N.Atluri

A Unification of the Concepts of the Variational Iteration,Adomian Decomposition and Picard Iteration Methods;and a Local Variational Iteration Method

Xuechuan Wang1,Satya N.Atluri2

This paper compares the variational iteration method(VIM),the Adomian decomposition method(ADM)and the Picard iteration method(PIM)for solving a system of first order nonlinear ordinary differential equations(ODEs).A unification of the concepts underlying these three methods is attempted by considering a very general iterative algorithm for VIM.It is found that all the three methods can be regarded as special cases of using a very general matrix of Lagrange multipliers in the iterative algorithm of VIM.The global variational iteration method is briefly reviewed,and further recast into a Local VIM,which is much more convenient and capable of predicting long term complex dynamic responses of nonlinear systems even if they are chaotic.

1 Introduction

The rapidly increasing interest of researchers in nonlinear problems has prompted a variety of analytical,semi-analytical and numerical methods.Among them,the variational iteration method(VIM)[Inokuti,Sekine and Mura(1978);He(1999)],the Adomian decomposition method(ADM)[Adomian(1988)]and the Picard iteration method(PIM)[Fukushimam(1997)](often combined with other approximation techniques,such as the modified Chebyshev-Picard iteration(MCPI)method[Woollands,Younes and Junkins(2015)])have received wide attention.Unlike in classical perturbation methods,these three methods do not depend on the existence of a “small parameter”in the nonlinear problem,and they are not limited to cases of weak nonlinearities.The applications of the three methods are relatively straightforward in that there is no need to determine the so-called small parameter or make linearization transformations to the original equation.Further,the results obtained with these methods are valid for the whole parameter domain.Thus they are regularly utilized in areas where the traditional techniques are not applicable.In literature,some comparisons have been made between them on the efficiency and scope of application.The advantages and disadvantages of each method are illustrated in papers[He(1999);Rach(1987)].

The VIM is capable of solving a large class of nonlinear problems,including both the systems expressed as either ordinary or partial differential equations.It is an analytical asymptotic approach[He(2006)],where the initial guess function is corrected step by step,and finally reaches the true solution.The correctional iterative formula of VIM is similar to that of the Newton-Raphson method,except that the former method is for functions while the latter is for fixed point of nonlinear algebraic equations(NAEs).From the view of Inokuti,Sekine and Mura(1978),we can see that the VIM is somehow an extension of the Newton method to the problem in function space.And the extension can also be made to problems expressed in algebraic,differential,integral,or finite-difference equations,or the combination of them.This idea is illustrated in detail and referred as the general use of Lagrange multipliers in Inokuti,Sekine and Mura(1978).However,for the case of general nonlinear terms,the derivation of exact generalized Lagrange multiplier is normally impossible.Considering that,the VIM of He[He(1999)]omits the nonlinearity in the adjoint equation satisfied by the generalized Lagrange multiplier.Other than that,the VIM of He[He(1999)]incorporates an artificial parameter in the approximation of the periodic solution.By eliminating the secular terms including the parameter,the accuracy of the result can be improved significantly.But this trick does not always work.As is illustrated in the section 3,it seems that only in some special cases can the approach show its efficiency.

The ADM is a decomposition method.It treats the solution as the sum of a series of functions,and decomposes the nonlinear terms into the rearranged Taylor series expansion in terms of Adomian polynomials.With an initial guess given,the solution is corrected in each iteration step by adding an integral of an Adomian polynomial.As the iteration proceeds,the nonlinear equation is solved gradually.This method provides great convenience for the calculation of the correctional function,but the construction of Adomian polynomials is somewhat complex,especially for the higher order terms.The conditions for convergence of this method have been discussed in literature.It should be noted that the method is just locally convergent because it is based on a Taylor series expansion.Some modifications were made to it by recursively applying it over divided time segments,so that the global convergence can be achieved[Ghosh,Roy and Roy(2007)].

Compared to VIM and ADM,Picard’s method takes a very simple form.How-ever,its application is very limited,since it needs to integrate the nonlinear terms in each iteration step,which could be very difficult to implement.Compared to Adomian’s method,the Picard iteration lacks the ease of computation and also the ability to solve a wide class of equations.But by combining with other computational techniques,it is still possible to make advances to PIM.For example,the MCPI method[Woolland,Younes and Junkins(2015)]combines the Chebyshev polynomials with the Picard’s method and is applied to the two body gravitational integration problem.It is shown that the integration process of Picard’s method becomes very simple and the method achieves high accuracy and efficiency.

Despite all the detailed differences in VIM,ADMand PIM,it is the objective of this paper to show that they are all not unrelated.As will be illustrated in section 2,the iteration formula of the Picard’s method and the ADM can be completely deduced from the iterative formula of the VIM.This indicates that a common mathematical principle,which is the general use of Lagrange multipliers,underlies these methods,and a unification of the concepts underlying the three methods can be elucidated.It will help to explain the similarity of the three methods,and how we can combine the ideas in VIM,ADM and PIM to achieve possibly better analytical asymptotic methods.

After that,a local variational iteration method(LVIM)is proposed in section 3.Firstly,the differential transform(DT)method[Jang,Chen and Liy(2000)]is introduced to help identify the generalized Lagrange multipliers.Then a piecewise solution is obtained by dividing the whole time domain into a finite number of small segments.The forcing term is approximated by a truncated Taylor series expansion in the LVIM,so that the calculation of integrals can be simplified.The advantages of the LVIM are as follows,

(1)The initial guess function can take a very simple form.Unlike the conventional VIM,there is no need to pay much attention to the construction of an initial guess.A linear function could be good enough for the LVIM,as long as it meets the boundary condition of the problem.

(2)Instead of restricting the nonlinear term from variation artificially,the nonlinear term can be included in the derivation of generalized Lagrange multipliers in the LVIM.So the correctional formula is more effective.

(3)The introduction of DT method provides the approximation of generalized Lagrange multipliers in Taylor series expansion.It makes the derivation of generalized Lagrange multipliers much simpler,and also provides convenience to the integration of the correctional formula.

(4)The LVIM has applicability to long term predictions of many kinds of complex nonlinear problems,including chaotic motions.

(5)The accuracy and computational speed of LVIM is relatively very high,even compared to the numerical methods such as RK4.

To convey the ideas in a simple and clear way,a system of first order differential equations is taken for illustration in this paper.However,the conclusions made in the following sections are also applicable to the higher order differential equations.It is well known that a higher order differential equation can always be transformed into a system of first order differential equations.For example,the equation

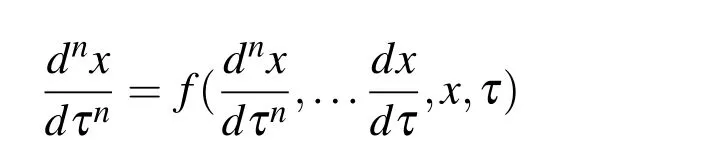
can be rewritten as a system of equations like

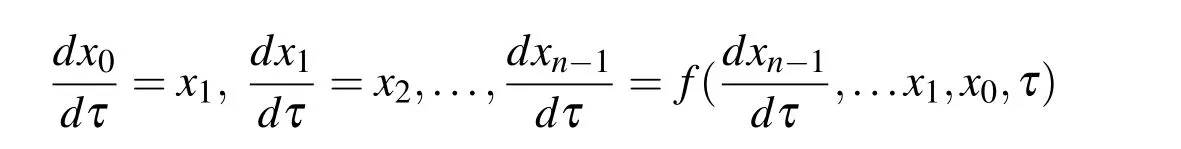
by introducing the variables x0,...xn−1.Therefore,the nonlinear ordinary differential equations can be expressed in a general form as

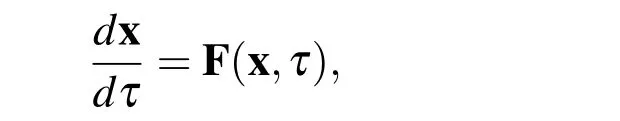
whereWhere,here onwards,a bold symbol indicates a vector or a matrix,and for brevity,the differential operatoris denoted asLin the following sections.

In the preceding equation,F(x,τ)is a nonlinear function of the state vectorxand the independent variable τ.

2 PIM,ADM,and VIM

The three methods,i.e.VIM,ADM and PIM,were proposed independently by different researchers at different times.ADM and PIM have been well known for a long time,while VIM has a history of no more than four decades.Although they appear to be unrelated to one another at first,a close examination leads to a unification of the three methods with the perspective provided by the concepts of VIM.In the following,the PIM and the ADM are briefly introduced.Then the VIM is described and some transformations are made to elucidate the relationships between all the three methods.

2.1 PIM

Consider an initial value problem(IVP)governed by a system of first-order differential equations

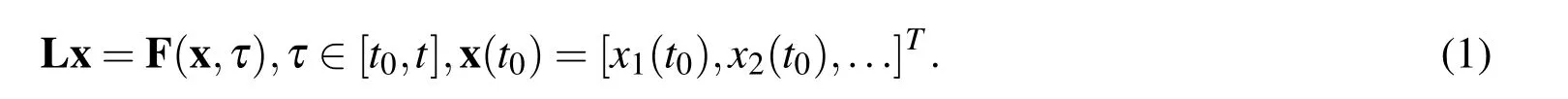
It is equal to the associated integral equations

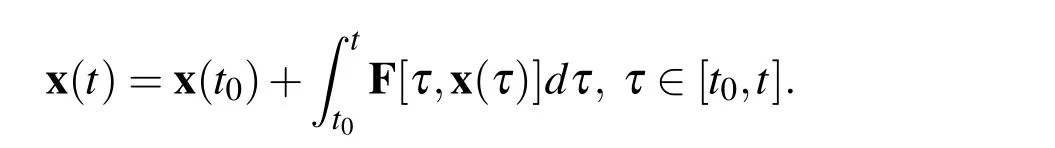
The PIM solves this problem in a recursive way by constructing a series of approximating functions.The process works as

(1)Give an initial guess of the solutionx0(τ)that satisfies the initial conditionx0(t0)=x(t0).

(2)Substitute it into the recursive formula that holds

for n≥0.

2.2 ADM

For convenience,we rewrite the dynamical system in the preceding IVP asLx=F(x,τ),whereLstands for the first-order derivative.LetL−1be the inverse operator ofL,namely the definite integrator.The equation can be recast as

withx(t0)being the initial condition.

The innovative part of ADM is that it approximates both the solution and the nonlinear part as sequences of functions and introduces the Adomian polynomials so that the original problem will be solved progressively.

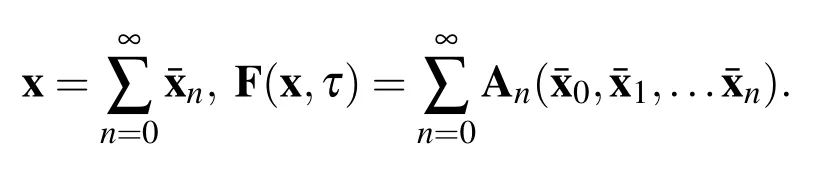
This enables us to rewritte the Eq.(3)as

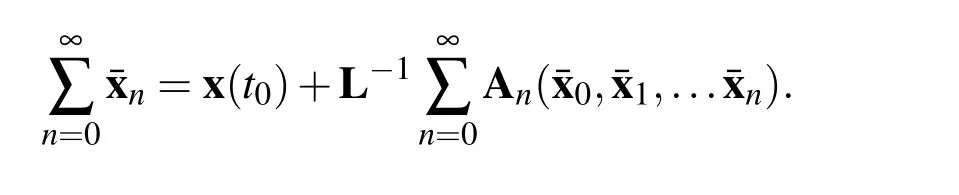
The solution can thus be derived recursively in the following way

The Adomian polynomialsAnare generated by simply rearranging the Taylor series expansion ofF(x,τ)about¯x0=x(t0).They are expressed as

2.3 VIM

Consider the following general nonlinear system

whereLis the first order differential operator andFis a nonlinear operator.The solution of this system can be approximated with an initial approximationx0(t)and the correctional formula as

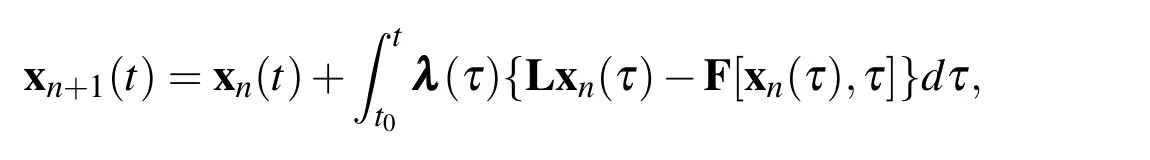
where λ (τ)is a matrix of Lagrange multipliers which are yet to be determined.Suppose Π [x(τ),λ (τ)]is a vector function ofx(τ)and λ (τ),where t0≤τ≤t.

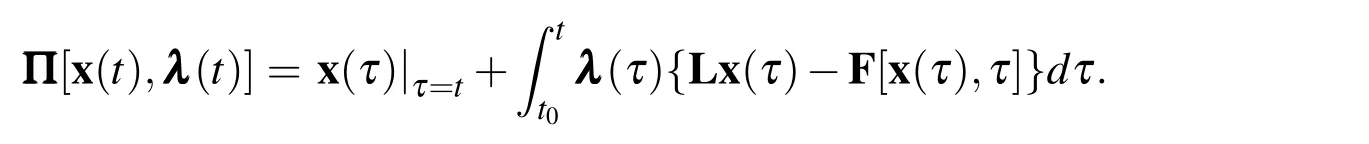
Letˆx(τ)be the exact solution ofLx(τ)=F[x(τ),τ].Naturally,it satisfies the expression

Now we want to make the function Π [x(t),λ (t)]stationary aboutxatx(t)=ˆx(t).Firstly,the variation of Π [x(t),λ (t)]is derived as

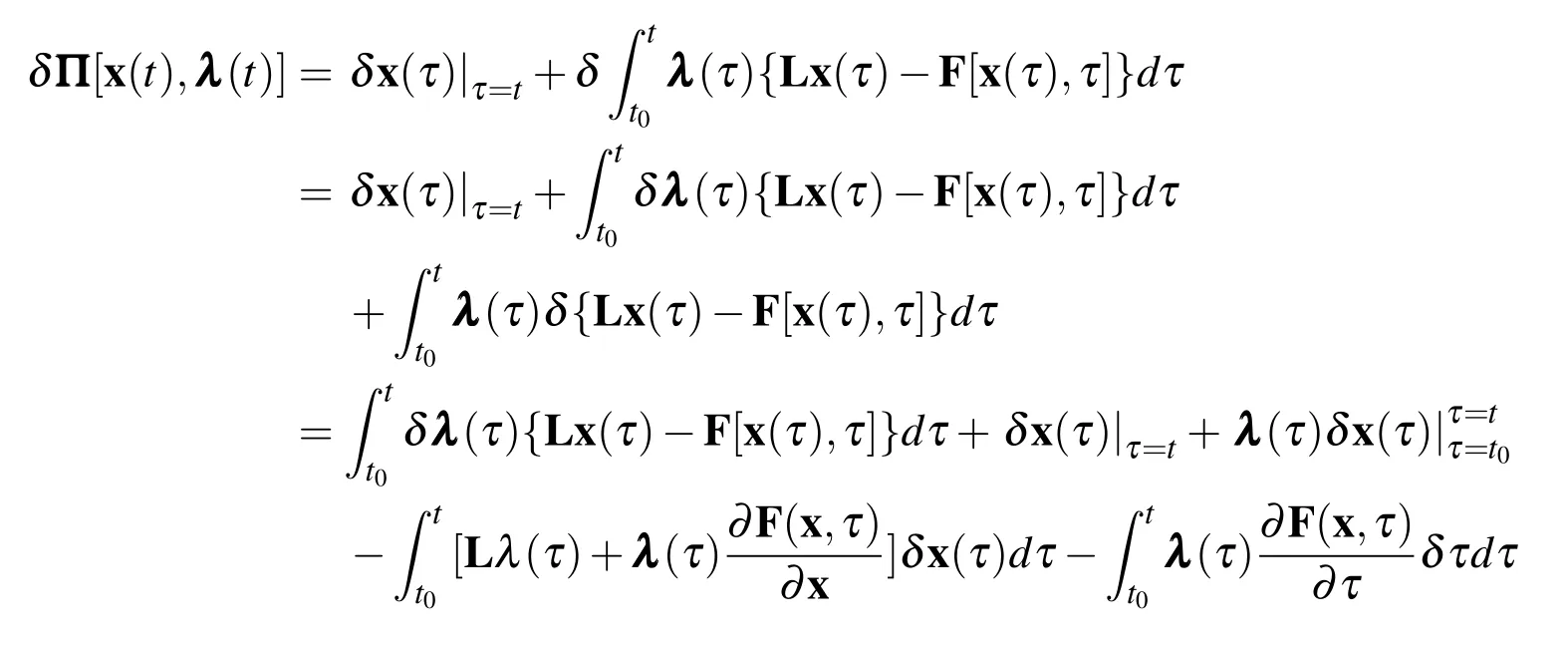
IfFis not an explicit function of τ,the term[∂F(x,τ)/∂τ]δτ can be omitted in the preceding formula.

Then we collect the terms including δx(τ)|τ=tand δx(τ),

Note that the boundary value ofx(τ)at τ=t0is prescribed,that is to say δx(τ)|τ=t0=0.Thus the stationary condition for Π [x(τ),λ (τ)]is obtained as

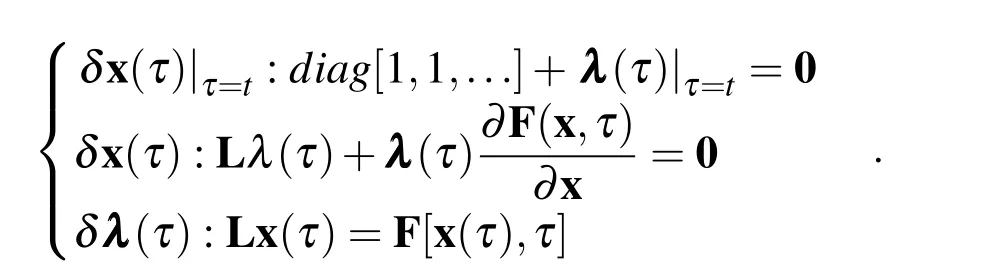
Noting that the exact solutionˆxis unknown,therefore the truly optimal λ (τ)is not available herein.As an alternative,λ (τ)is approximated by replacingˆxwithxn.Ifxnis a neighbored function ofˆx,i.e.ˆx−xn=δˆx,the error caused will not exceed O2(δˆx).

In the VIM of He(1999),sometimes the nonlinear term is considered as restricted from variation,in order to simplify the calculation of λ .As an asymptotic method for solving nonlinear problems,VIM provides plenty of freedom to the user.It does not restrict the selection of initial guess functions and even allows the existence of unknown parameters in it.Further,depending on the selection of a restricted variation,the matrix of generalized Lagrange multipliers λ can be determined in various ways.The less restricted the variational terms are,the more accurate will the Lagrange multipliers be.

3 VIM and its relationship to PIM and ADM

Instead of PIM,if VIM of He[He(1999)]is utilized to solve the IVP governed by Eq.(1),we will get the corresponding correctional formula with λ

where˜F(xn,τ)is considered as being restricted from variation.The matrix of Lagrange multipliers λ are determined from the following restricted stationary conditions:

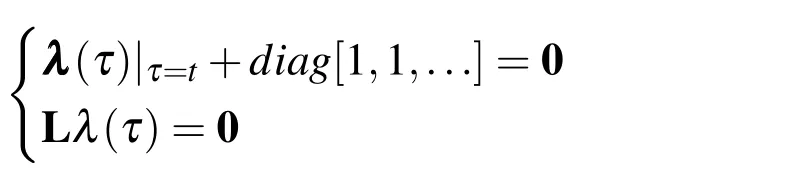
The Lagrange multipliers,therefore,can be identified as λ (τ)=diag[−1,−1,...].As a result,we obtain the following iteration formula

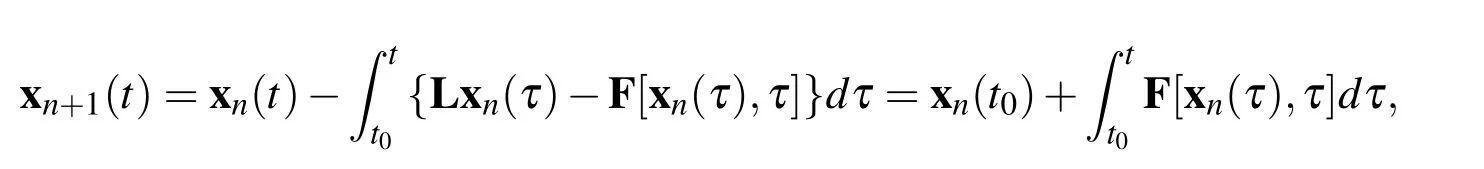
Noting thatxn(t0)is equal to the initial valuex(t0),it is exactly the Picard iteration.In the paper of He(1999),a first-order differential equation is considered and the ADM is proved to be a specific version of VIM.This work is reviewed in the following.

Consider the equation Lx+Rx+Nx=g(τ),in which L is a first-order differential operator,while R is a linear operator.For this equation,the correctional formula of VIM is

Considering Rxn+Nxnas restricted from variation,λ can be easily obtained as−1 in this case.Suppose x0=¯x0=x(t0)+L−1g(τ),substituting it into the formula gives

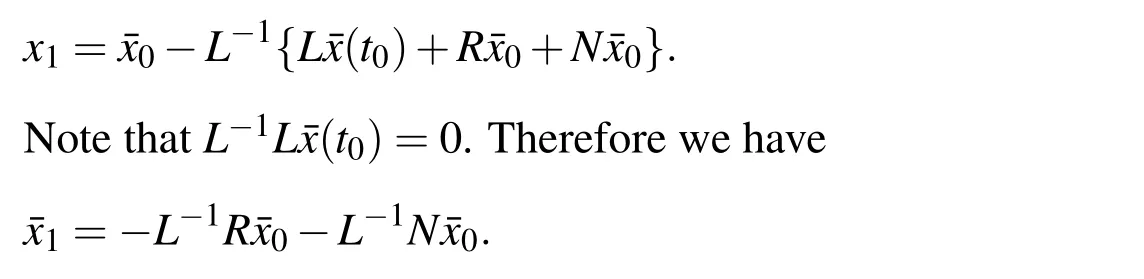
Similarly the iteration process gives

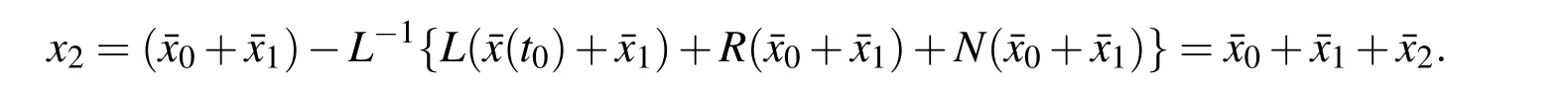
If¯x1is regarded as relatively small,expanding the nonlinear functional about¯x0and ignoring the higher-level small functions leads to N(¯x0+¯x1)=N(¯x0)+¯x1N′(¯x0).Then we have

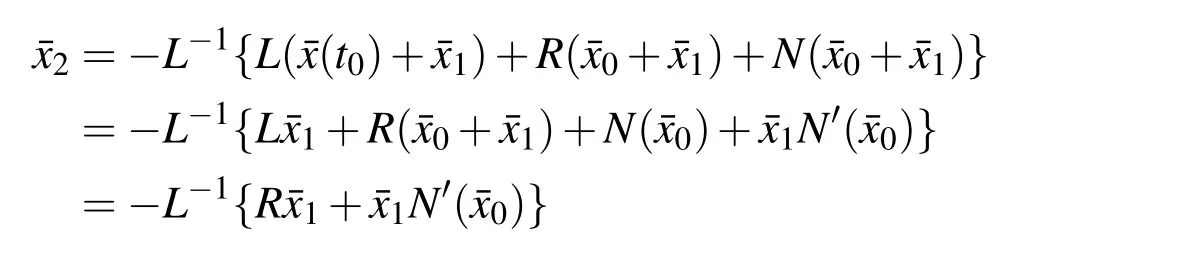
Further,in the nth step of iteration,regard¯xn−1as the relatively small function and omit the terms O(¯xm1¯xm2...¯xmk),where m1+m2+...+mk≥n.It leads to the correctional formula of ADM.

It is worth to note that the above comparison can also be made in the case of multidimensional system.Herein,a general form of the nonlinear ordinary differential equations is taken for illustration.

Lx=F(x,τ),

The ADM gives an iteration formula as

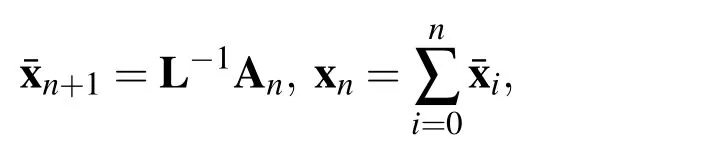
while the correctional formula of VIM is

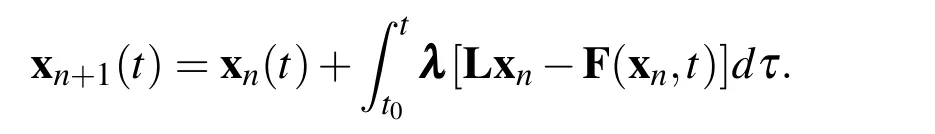
Set λ as diag[−1,−1,...]and follow the manipulations we made to the one dimensional case.Supposex0=¯x0,from the correctional formula of VIM we have

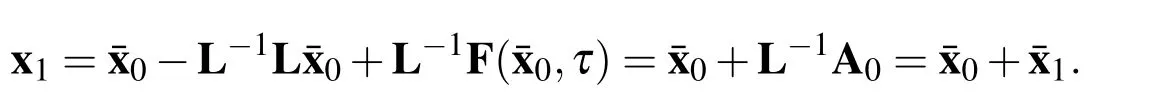
Accordingly,

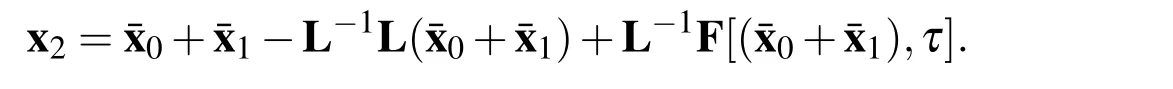
Regard¯x1as a relatively small amplitude vector of functions.The nonlinear term can be rewritten as

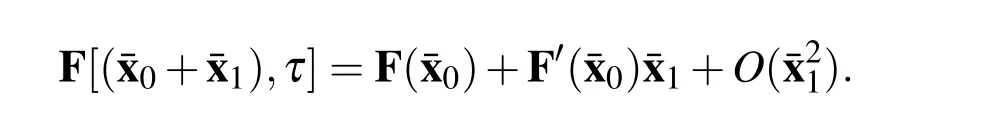
Omitting the small terms O(¯x21),it leads to

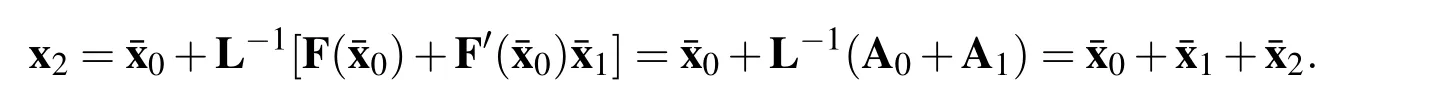
As the iteration goes on,we have

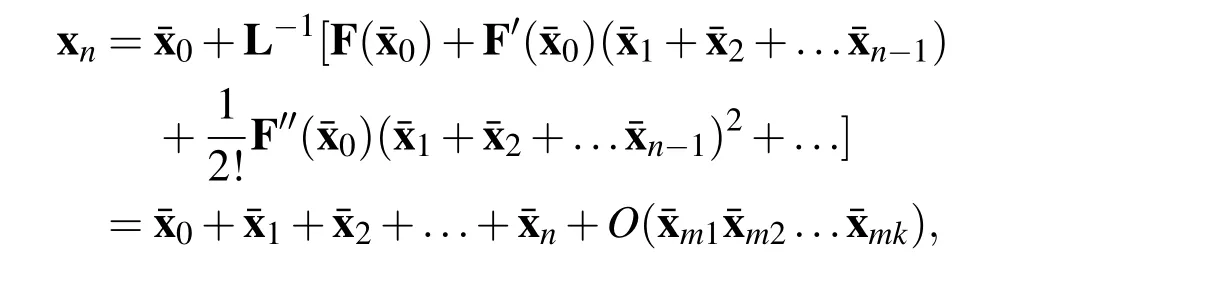
which becomes the ADM correctional formula by omitting the small terms

From the statements above,it is clear that the ADM and PIM can both be regarded as variants of VIM.Although they are treated as different methods in literature,and were developed into various forms such as modified ADM and MCPI method,a common principle,namely the general use of Lagrange multipliers guides all of them.

4 Local variational iteration method

4.1 Limitations of Global VIM

It has been shown that the VIM is effective in approximating the periodic motions of nonlinear systems,especially the limit cycle oscillation.To verify that,an unforced Duffing equation is solved with VIM herein.The governing equation is

where c=0,k1=1,k2=1.

In the approach proposed by He(1999),the Lagrange multiplier λ is derived with the nonlinear term being restricted from variation,and it is shown to be tenable in the unforced case with the initial conditions x1(t0)=A,x2(t0)=0 and initial guess x1(t)=Acosωt.The correctional formula is

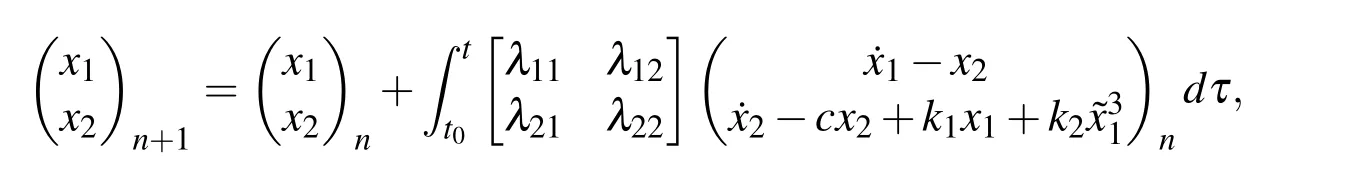
With the nonlinear term˜x31restricted from variation,the matrix of Lagrange multipliers satisfies the condition:

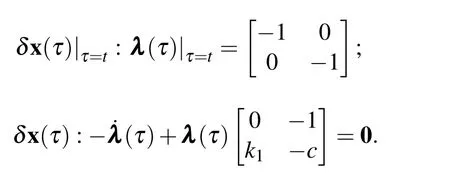
Therefore,the matrix of Lagrange multipliers λ (τ)is identified as

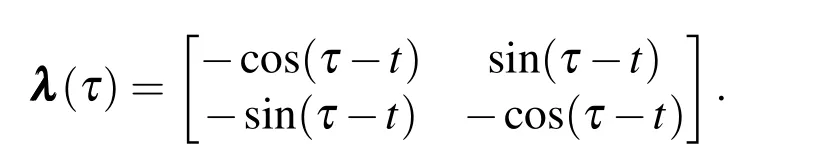
The solution corrected only once with VIM can already give a result comparable with that of the RK4 method.The example of an unforced Duffing equation shows that the VIM could be very efficient in approximating the periodic solution of nonlinear systems by eliminating the secular term appearing in the correctional formula.The numerical results are plotted in Fig.1 with the initial condition x(0)=1,˙x(0)=0 and initial guess x1(t)=cosωt.By substituting the initial guess into the correctional formula of VIM,we can obtain a corrected solution,of which the secular term is(2−17ω2+9ω4)cos(t).To eliminate the secular term,the frequency is determined to be ω=1.32774.

However,in a more general case withx(t0)=?A B?T,the performance of VIM is far inferior to the preceding one.The initial guess is selected as x(t)=Acosωt+(B/ω)sinωt.Let A=1 and B=1,the variational iteration formula gives the corrected solution,in which the terms of sint and cost are

It is easily identified that the coefficients of sint and cost can not both be equal to zero.Here only the term of cost is eliminated,leading to the approximation ω≈1.4493.Substituting it into the corrected solution,we have x1(t)=1.00598cos(1.4493t)−0.00597962cos(4.34791t)−0.111705sin(t)+0.694112sin(1.4493t)+0.0243163sin(4.34791t).

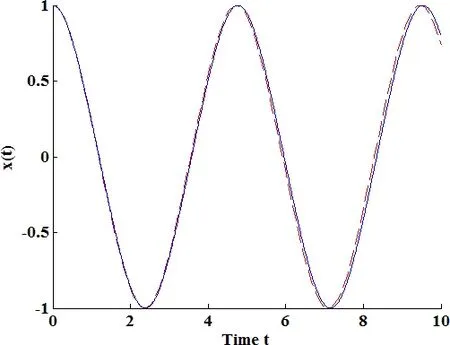
Figure 1:Comparison of VIM and RK4.solid line:RK4.Dash line:VIM

This result is compared with that of RK4 in Fig.2.

It is believed that if both terms of sint and cost vanish,the corrected solution will be more accurate.But with just one parameter ω in the initial guess,this will be an impossible mission.Thus we tried to bring in two parameters ω1, ω2in the initial guess,which takes the form x1(t)=Acosω1t+(B/ω2)sinω2t.If the resulted corrected solution can be obtained analytically,the accuracy will be much improved.But along with it,the calculation of variational iteration formula will become much more complex.We found that even with the help of Mathematica,this job is still too burdensome to be accomplished.

Moreover,it is also indicated that a carefully selected initial guess is important to ensure the convergence of this method.If the approximate function takes the form as x1(t)=A+Bt rather than x1(t)=Acosωt,the result given by VIM will be more and more divergent from the true solution with the iteration.It is illustrated in the case A=1 and B=1.With VIM,the initial guess x1,0(t)=1+t is corrected for 2 times and the results are given as follows.

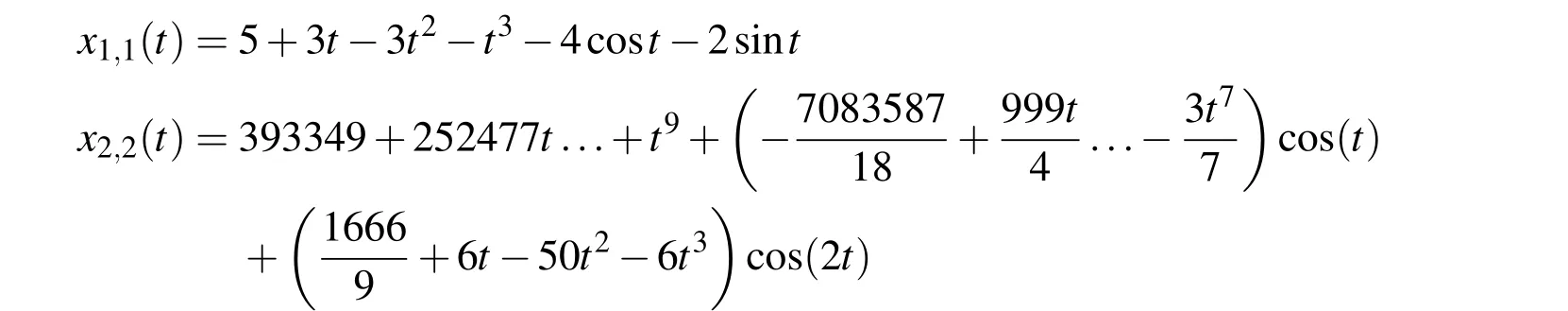
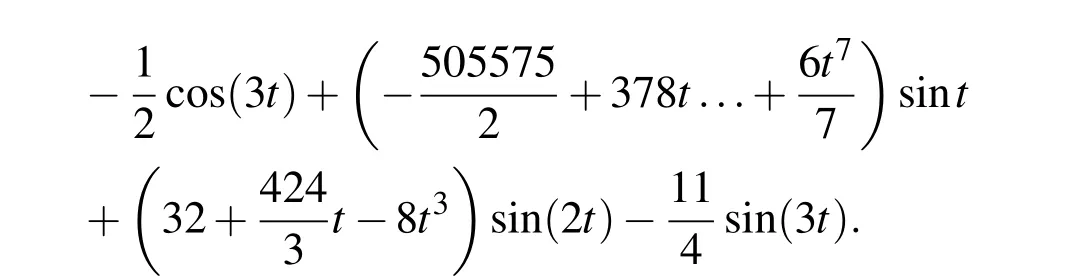
The solution x1,1(t)is compared with that of RK4 in Fig.3.

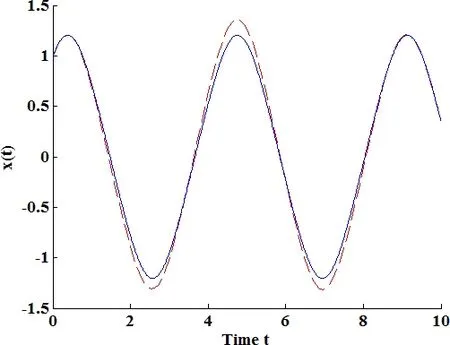
Figure 2:Solid line:RK4.Dash line:VIM

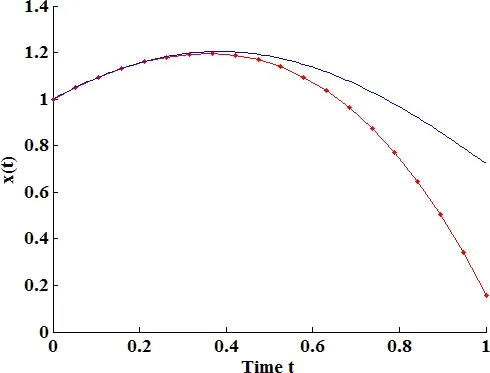
Figure 3:Solid line:RK4.Dotted line:VIM

The above numerical examples and analysis show that VIM is fastidious to the initial condition of the problem,and also too sensitive to the initial guess function,which is analogous to the Newton’s iteration method for solving nonlinear algebraic equations(NAEs).This method also fails to predict the long term responses of some complex nonlinear phenomenon such as chaos or quasi periodic motion,because these patterns of motion are non-periodic and can hardly be approximated by any analytical functions.

4.2 Methodology of LVIM

As is shown in Atluri (2005)and Dong,Alotaibi,Mohiuddine and Atluri(2014),local approximations are far more effective in solving initial value and boundary value problems.We use these ideas in developing a local variational iteration method.To remedy the drawbacks shown above,we propose to further improve the VIM.Here is the primary idea.Firstly,the nonlinear term should be kept in the derivation of Lagrange multipliers so that a better correction can be obtained for arbitrary approximation.And then the entire time domain is divided into small intervals and the LVIM is applied repeatedly in each time interval ti−1≤ τ≤ti.In each interval ti−1≤ τ≤ ti,we approximate locally using an arbitrary functionx(τ)=A+Bτ for instance;then the corrected solution will be a function ofAandB,i.e.the initial condition of each interval,thus the solution in the entire time domain can be obtained by the repetition ofAandBstep by step.

With this in mind,the IVP of the unforced Duffing equation is solved with the initial condition as x1(t0)=1,x2(t0)=1.The correctional formula is

where ti−1≤ t≤ ti.The stationary condition is

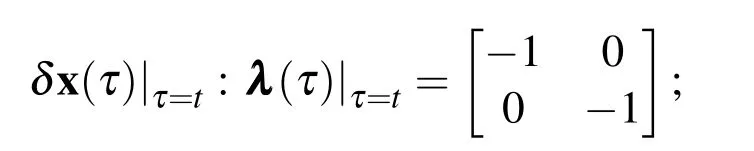
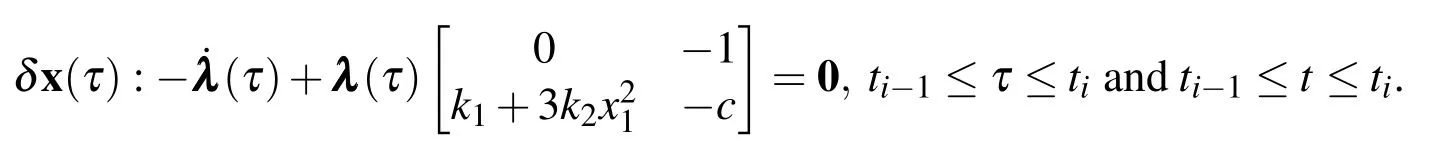
Instead of neglecting the nonlinear term,we kept it in the derivation of λ .This makes the differential equations more difficult to be solved analytically.But an exact analytical solution is not necessary here.The differential transform(DT)method is introduced to obtain the approximated λ in the form of power series.With the nonlinear term included,the approximated λ is actually more precise than that in the VIM of He(1999).

Supposing that the initial guess of x1takes the form as x1,0(τ)=Bτ+A,an approximated λ can be obtained using the DT method.Herein only the first four DT terms of λ (τ)is kept.

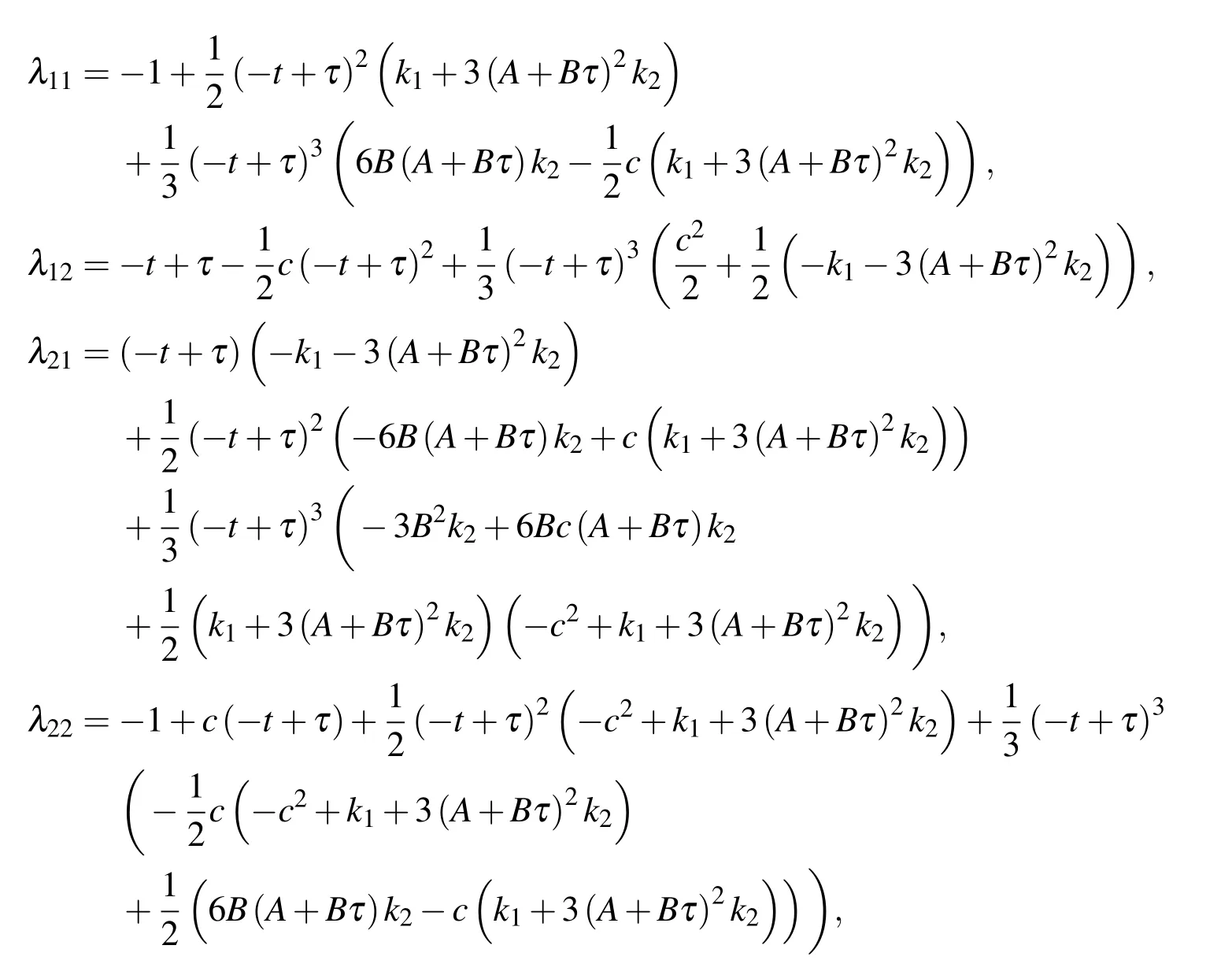
where ti−1≤ t≤tiand ti−1≤ τ≤ti.Using the correctional formula for one time,we have

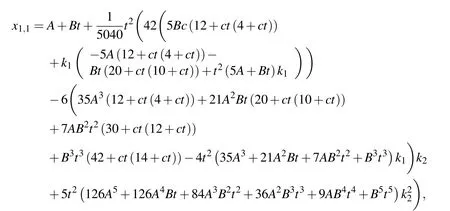
where ti−1≤ t≤ ti.

In Fig.4(a),the preceding solution is compared with the numerical results obtained by ODE45,for which the relative and absolute accuracy are both set as 10−15.Fig.4(b)shows the computational error of the LVIM with respect to ODE45.The time step size is set as Δt=0.01 and the simulation is carried in t=[0,100].From Fig.4(b),it can be seen that the error of the LVIM is less than 10−3even for t=100.

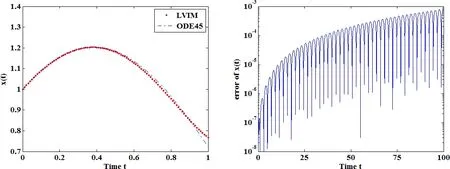
Figure 4:Comparison of the LVIM and the ODE45.

To further inspect the performance of the LVIM in predicting complicated responses,the forced Duffing equation is investigated.

It is shown to be a chaotic system by RK4 and other reliable methods.Unsurprisingly,the VIM of He[He(1999)]fails to solve it because the solution is too complicated to be computable.An approximation is made to the forced term of the system.Since it is involved in the integration,a simple form of it will accelerate the calculation.For that,the forced term is expanded into power series as well.The stationary condition for λ is

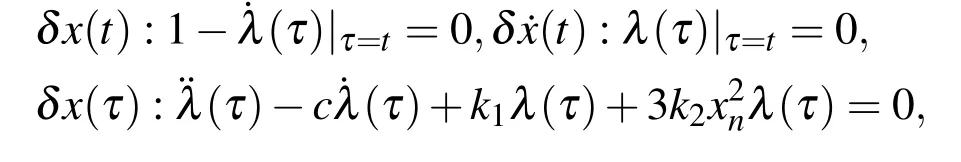
where ti−1≤ τ≤tiand ti−1≤t≤ti.

Suppose the initial guess in each interval ti−1≤ τ≤ tiis x0(τ)=A+Bτ.With DT method,we can get the fourth-order approximated λ(τ,t)in terms of A and B,which is

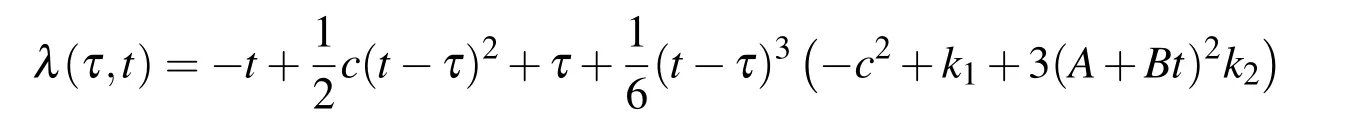
Then substituting it into the correction formula,with the forced term being replaced by power series,will lead to the corrected function x1(t)

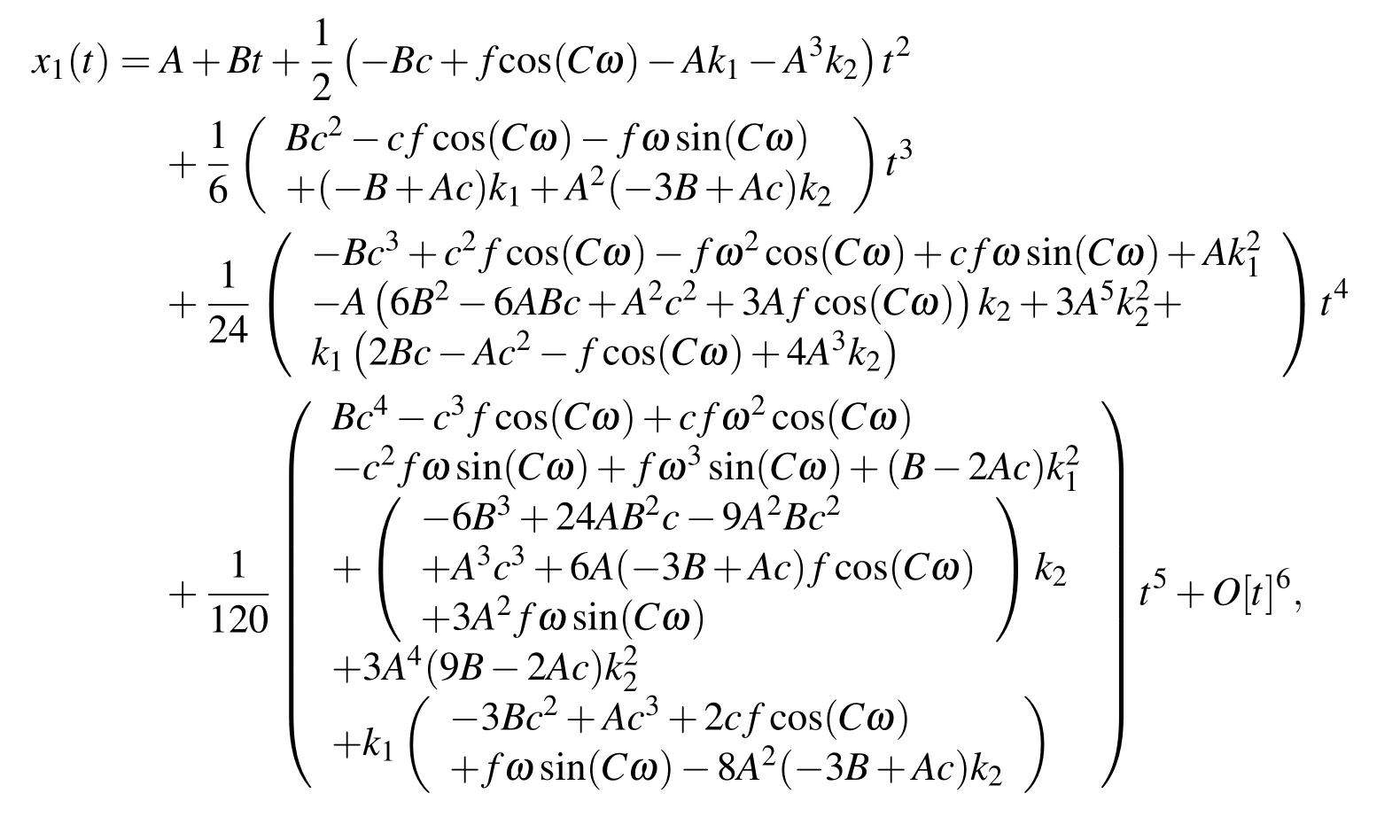
where ti−1≤ t≤ ti.It has a compacted form with A,B,ti−1(denoted as C in the corrected function)as the coefficients.When applied to multiple time intervals,it only needs to recompute A,Band t0,which correspond to the final position,velocity and time instant of the last interval.The LVIM is very fast,precise and efficient on solving nonlinear problems.Fig.5 shows the chaotic motions of a forced Duffing oscillator predicted by both LVIM and RK4 methods.The time step size of LVIM is set as 0.2,while that of RK4 needs to be set as 0.02 in order to achieve the same accuracy.The numerical simulation carried out with MATLB shows the LVIM is almost 10 times faster than RK4 in this case.The computation time of the LVIM and the RK4 are 0.013471s and 0.135445s,respectively.

Similar to the modified ADM,the variational iteration method is further improved herein by bringing in some local approximation techniques,so as to be practical in predicting long term motion and complex dynamical responses.The LVIM makes the derivation of Lagrange multipliers λ and the calculation of the variational iteration formula much simpler,yet still provide reliable solution in each sub time domain.

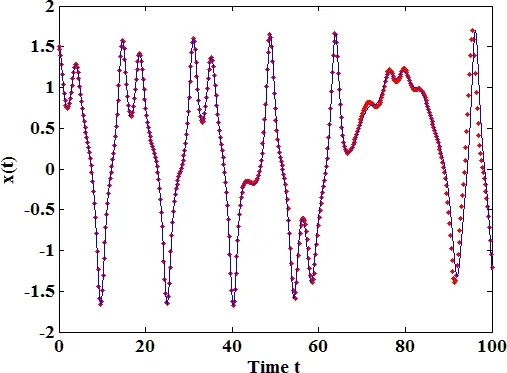
Figure 5:Comparison of the LVIM and the RK4 method for the forced Duffing oscillator.Dots:LVIM.Solid line:RK4

5 Conclusions

The Picard iteration method,the Adomian decomposition method and the variational iteration method are unified in this paper.From the view point provided by the concept of generalized Lagrange multipliers,it is found that the three methods are rooted in the same mathematical approach of generalized Lagrange multipliers.By some simple transformations,the Picard iteration formula and Adomian decomposition formula can be derived from the variational iteration formula.

However,the Global VIM is very laborious in practice and is unable to predict long term responses of nonlinear systems,although it is able to provide an analytical solution.Being aware of that,we introduced a Local VIM that simplified the derivation of the matrix of generalized Lagrange multipliers λ with the DT method.By dividing the entire domain into small intervals and updating the initial conditions in each sub-interval,the Local VIM method achieves very high accuracy and very high computational speeds.

Acknowledgement:The support of Texas Tech University,as well as the support of the Chinese Scholarship Council to the first author are gratefully acknowledged.

Adomian,G.(1988):A review of the decomposition method in applied mathematics.Journal of Mathematical Analysis and Applications,vol.135,pp.501–544.

Atluri,S.N.(2005):Methods of Computer Modeling in Engineering&The Sciences,Volume I.Tech Science Press,Forsyth.

Dong,L.;Alotaibi,A.;Mohiuddine,S.A.;Atluri,S.N.(2014):Computational methods in engineering:a variety of primal&mixed methods,with global&local interpolations,for well-posed or Ill-posed BCs.Computer Modeling in Engineering&Sciences,vol.99,no.1,pp.1–85.

Fukushimam,T.(1997):Picard iteration method,Chebyshev polynomial approximation,and global numerical integration of dynamical motions.The Astronomical Journal,vol.113,no.5,pp.1909–1914.

Ghosh,S.;Roy,A.;Roy,D.(2007):An adaption of Adomian decomposition for numerical-analytic integration of strongly nonlinear and chaotic oscillators.Computational Methods in Applied Mechanics and Engineering,vol.196,pp.1133–1153.

He,J.(1999):Variational iteration method:a kind of non-linear analytical technique:some examples.International Journal of Non-linear Mechanics,vol.34,pp.699–708.

He,J.(2006):Some asymptotic methods for strongly nonlinear equations.International Journal of Modern Physics B,vol.20,no.10,pp.1141–1199.

Inokuti,M.;Sekine,H.;Mura,T.(1978):General use of the Lagrange multiplier in nonlinear mathematical physics,in:S.Nemat-Nasser(Ed.),Variational Method in the Mechanics of Solids.Pergamon Press,Oxford,pp.156–162.

Jang,M.;Chen,C.;Liy,Y.(2000):On solving the initial-value problems using the differential transformation method.Applied Mathematics and Computation,vol.115,pp.145–160.

Rach,R.(1987):On the Adomian decomposition method and comparisons with Picard iteration.Journal of Mathematical Analysis and Applications,vol.128,pp.480–483.

Woollands,R.M.;Younes,A.B.;Junkins,J.L.(2015):New solutions for the perturbed lambert problem using regularization and picard iteration.Journal of Guidance,Control,and Dynamics,vol.38,no.9,pp.1548–1562.

1Texas Tech University;Center for Advanced Research in the Engineering Sciences;Visiting Scholar from Northwestern Polytechnical University,China.

2Texas Tech University;Center for Advanced Research in the Engineering Sciences.