压电陶瓷型光栅解调仪双边沿解调修正方法

张 俊

(湖北省交通运输厅武黄高速公路管理处,武汉 430205)

压电陶瓷型光栅解调仪双边沿解调修正方法

张 俊

(湖北省交通运输厅武黄高速公路管理处,武汉 430205)

为了提高光纤光栅解调仪表的速度与精度,提出了一种双边沿解调及非线性修正方法对PZT(压电陶瓷)的迟滞效应进行补偿。通过对PZT两端电压的上升、下降沿同时采集数据并进行交叉解调的方式,在提高解调速度的同时有效地消除了迟滞效应。利用1个10探测点的C波段光栅对该修正方法进行检验,修正效果较为理想,各波长的解调误差小于±5 pm。

压电陶瓷;迟滞效应;双边沿;非线性修正

0 引 言

可调谐波长滤波器是光纤光栅解调仪表中的核心器件,其种类繁多,包括电流调谐型、电压调谐型和PZT(压电陶瓷)型等[1]。其中PZT型由于具有响应速度快、不发热和推力大等诸多优点[2],其与法布里―珀罗结构相结合,通过PZT改变两个反射镜之间的距离能实现可变的波长输出[3-4]。以该类型可调谐波长滤波器为核心的光纤光栅解调仪表被称为PZT型光纤光栅解调仪,它在光纤传感领域的应用颇为广泛,可以用于温度、震动和应力等环境变量的测量[5-6]。但由于PZT的“电压―位移”曲线为迟滞非线性[7],迟滞效应引入的非线性失真影响了仪表的解调精度,严重地限制了PZT型光纤光栅解调仪表的发展。

目前针对PZT迟滞效应的非线性修正的研究较多,并且绝大多数都是对PZT的非线性轨迹进行建模,比如长春光学精密机械与物理研究所提出了一种Duhem模型,通过逆补偿与增量PID(比例积分微分控制)复合控制,实现对PZT系统的迟滞非线性误差校正[7-8];中国科学院光电技术研究所对前人提出的经典PI(π)模型进行了修正,以适用于自身的PZT器件[9-10],但不同的PZT,其轨迹模型一定存在差异,即使再完美的模型也无法适用于所有的PZT。为提高PZT型光纤光栅解调仪的性能,本文提出了一种双边沿解调及非线性修正方法,能够通过反馈的方式实时地修正PZT的迟滞效应,该方法适用于任何类型的PZT,并能达到较好的修正效果。

1 系统原理

PZT型光纤光栅解调仪一般采用对称三角波对PZT进行驱动,但PZT在三角波上升沿和下降沿期间的位移并不一致,其电压―位移曲线如图1所示。

图1 PZT的电压─位移曲线

PZT型光纤光栅解调仪基本原理如图2所示。

图2 PZT型光纤光栅解调仪表的基本原理

宽带光源发出的光信号经PZT型可调谐波长滤波器后被调制成扫频光,经一个分路器后同时通过待测光栅和2 nm波长间隔的标准光学栅格生成器,最后被数据采集卡采集,通过对比分路后的波形即可解出待测光栅的实时波长。图1中PZT的迟滞效应会导致经过2 nm标准波长间隔光学栅格生成器后的波形失真,造成各波长之间间隔不等,严重影响了待测光栅的解调结果,其波形图如图3所示,图中矩形框区域内可轻易地判断出间隔不等即失真,若不采取任何修正方法,则会严重影响解调精度,造成较大误差甚至错误的结果。

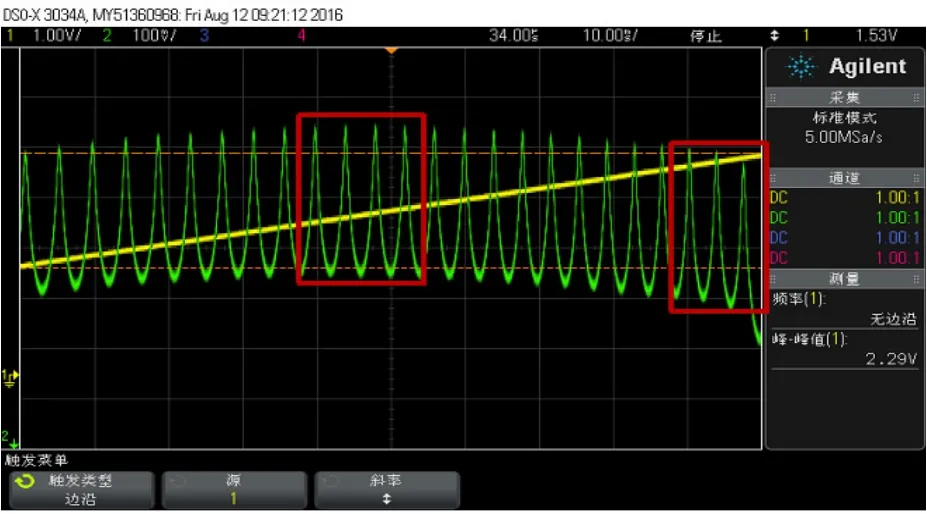
图3 经过2 nm波长间隔的标准光学栅格生成器后的波形

2 修正方法

本文所提出的双边沿解调修正方法的具体流程如图4所示。

图4中待测与标准波长分别为通过待测光栅后的波形和通过2 nm波长间隔的标准光学栅格生成器后的波形。2 nm波长间隔的标准光学栅格生成器为无源器件,其额定波长值为已知,令其为绝对参考值Ds;令上升沿采集到的标准波长数组为Du-s(上升沿的相对参考值),待测波长数组为Du-m;下降沿采集到的标准波长数组为Dd-s(下降沿的相对参考值),待测波长数组为Dd-m。

首先假设不存在迟滞效应,上升沿的标准光谱数组Du-s与绝对参考值Ds完全一致,即Du-s=Ds。将下降沿的标准光谱与上升沿的标准光谱进行对比,由于Du-s=Ds,即每个波长均为已知且两波长之间间距为2 nm,根据线性插值的方法可以计算出下降沿的标准光谱数组Dd-s。若不存在任何迟滞效应,则下降沿的标准光谱数组Dd-s与绝对参考值Ds应完全一致,但由于迟滞效应的存在,Dd-s≠Ds;将Dd-s与Ds进行逐峰作差可获得上升沿修正数组Du-c,最后再使用Du-c对上升沿的标准光谱数组Du-s进行修正,即可完全消除迟滞效应的影响,其中Du-c、Du-s和Ds应满足:

图4 双边沿解调修正流程图

由于该修正过程是利用下降沿的标准光谱来修正上升沿的标准波长参考值,因此称其为双边沿修正。上升沿标准光谱的相对参考值Du-s会根据式(1)和式(2)实时进行修正,最后使用线性插值法对下降沿的待测光谱Dd-m进行解调。此时根据Du-s计算出的Dd-s与绝对参考Ds一致,因此根据Du-s计算出的Dd-m为绝对准确的波长。这种用上升沿标准光谱对下降沿待测光谱进行解调的方法称之为双边沿解调。

同理可利用上升沿的标准光谱来修正下降沿的标准波长参考值,最后利用修正后的下降沿标准波长参考值Dd-s对上升沿的待测光谱Du-m进行解调。该方法不仅消除了迟滞效应带来的非线性失真,使解调结果更加精确,而且将解调速度提升到单边沿方式的两倍。

图5所示为双边沿修正法示意图。

图5 双边沿解调修正法示意图

3 修正结果

为对双边沿交叉解调及修正方法的实际效果进行检验,以该方法为基础对一已知波长的10个O波段光栅进行测量,其实际波长值与解调波长值的对比如表1所示。

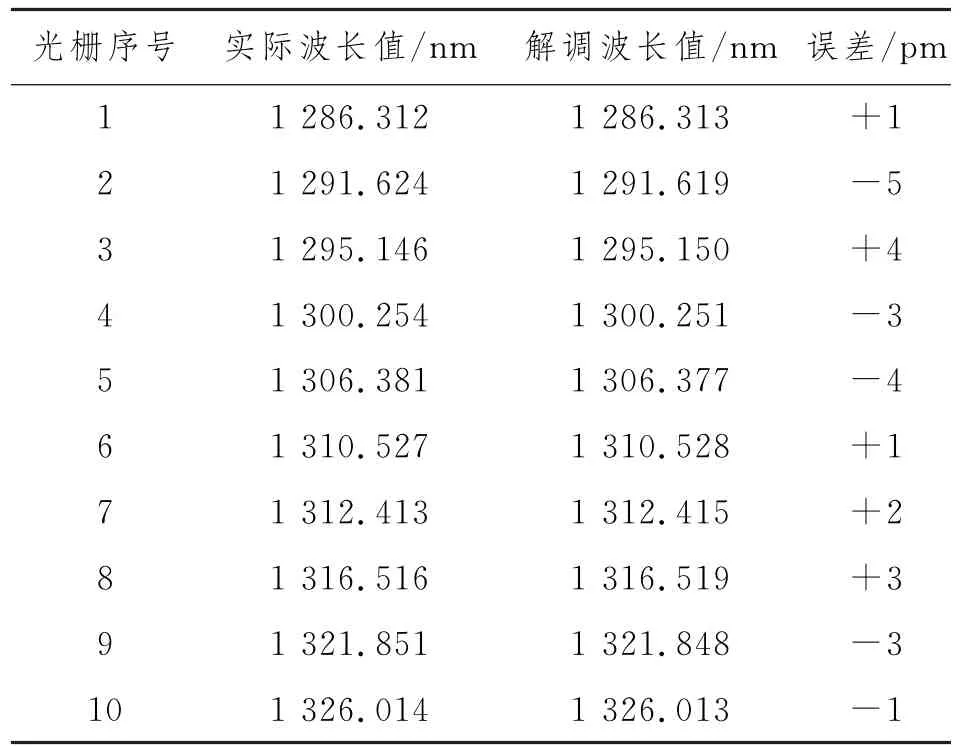
表1 10点光栅的实际波长值与解调波长值

由表1可知,解调误差为―5～+4 pm,已达到仪表本身的测量误差(长时间波长稳定性在±5 pm以内)。该实验结果表明,双边沿解调及修正方法的效果良好,基本消除了PZT迟滞效应带来的误差。

4 结束语

近年来,光纤传感行业的发展十分迅猛,在火灾报警、周界安防、应力监测和声波测量等领域都有着广泛的应用。PZT型光纤光栅解调仪表具有响应速度快、波长分辨率高和成本低等优势,有着广阔的发展前景。但PZT的迟滞效应是这一技术推广和应用的主要难点。本文提出了一种双边沿解调修正方法对迟滞效应进行修正,利用上升沿和下降沿的交叉解调修正,有效消除了迟滞效应给解调带来的影响,并且适用于所有类型的PZT个体,使该类型光纤光栅解调仪表可达到更高的精度从而拓展高端的应用市场。

[1]姚文娟.基于光纤布拉格光栅的流量传感器研究[D].大连:大连理工大学,2012.

[2]王喜昌,庞启,徐文军,等.基于线性滤波器的布拉格光纤光栅解调系统的稳定性[J].光学精密工程,2013,21(11):2785―2790.

[3]Bao P,Yuan M,Dong S,et al.Fiber Bragg grating sensor fatigue crack real-time monitoring based on spectrum cross-correlation analysis[J].Journal of Sound &Vibration,2013,332(1):43―57.

[4]Jeong H M,Lee J R.Design of resonant acoustic sensors using fiber Bragg gratings[J].Measurement Science and Technology,2010,21(21):57001―57006.

[5]尹国路,娄淑琴,彭万敬,等.光纤布拉格光栅法布里―珀罗干涉式传感器灵敏度[J].中国激光,2010,37 (6):1490―1495.

[6]王江峰.光纤光栅感温火灾探测报警系统在原油罐区的应用[J].自动化应用,2006,36(11):56―57.

[7]孙孔政,徐抒岩.PZT系统迟滞非线性建模与控制的研究[D].长春:中国科学院研究生院(长春光学精密机械与物理研究所),2013.

[8]姜刚.PZT非线性迟滞模型研究[D].苏州:苏州大学,2014.

[9]王耿,饶长辉,官春林.压电驱动器非线性校正技术研究[D].成都:中国科学院研究生院(光电技术研究所),2013.

[10]秦海辰.PZT驱动的运动平台建模与控制研究[D].武汉:华中科技大学,2014.

A Double-Edge Demodulation and Correction Method of the PZT Type Grating Demodulation Instrument

Zhang Jun
(Wuhuang Expressway Management Office,Department of Transportation of Hubei Province,Wuhan 430205,China)

In order to improve the demodulating speed and precision of the instrument,this paper propose a double-edge demodulation and nonlinear correction method to modifythe hysteresis effectof the piezoelectric ceramic.The demodulating speed and accuracy of the instrument has been improved by a cross-demodulation method using the data at rising edge and failing edge of triangle voltage at the same time.The effectiveness of thenonlinear correction method has been verified using a C band grating with 10 detection points.It is found that the wavelength demodulation error is less than±5 pm.

PZT;hysteresis effect;double-edge;nonlinear correction

TN247

A

1005-8788(2016)06-0053-03

10.13756/j.gtxyj.2016.06.015

2016-07-25

张俊(1979―),女,湖北荆门人。高级工程师,主要从事智能交通关键技术、设备的研究与工程应用。