基于模拟退火算法的改进型退火策略研究
宁德圣, 曾 光, 雷 莉, 许 曦
(东华理工大学理学院,江西 南昌 330013)
基于模拟退火算法的改进型退火策略研究
宁德圣, 曾 光, 雷 莉, 许 曦
(东华理工大学理学院,江西 南昌 330013)
研究模拟退火算法中的降温策略,将一种类似于多普勒效应型温度递减曲线作为退火降温曲线,有效避免了传统模拟退火算法极易陷入局部极小值的缺陷。通过增加记忆功能使搜索全局最优解的质量得到提高。最后,利用这种新的算法对TSP问题进行了数值模拟,实验结果表明,该降温策略的性能确实优于传统降温策略。
模拟退火算法; 降温策略; 多普勒型; 记忆功能
宁德圣,曾光,雷莉,等.2016.基于模拟退火算法的改进型退火策略研究[J].东华理工大学学报:自然科学版,39(3):298-300.
Ning De-sheng, Zeng Guang, Lei Li,et al.2016.Modified strategy of cooling based on simulated annealing algorithm[J].Journal of East China University of Technology (Natural Science), 39(3):298-300.
模拟退火算法是经典的组合优化算法,一般在较高温度的状态下采用Metropolis抽样准则随机寻找最优解,同时利用降温过程来进行重复的抽样过程,直到得到满足相近最优值。然而这种算法依然存在着其自身的不足, 例如算法运行时间过长、在局部最优处终止不前以及解空间的搜索能力和范围有限等缺陷。陈华根等(2006)、吴进波等(2007)从退火策略的角度出发,提出了一种带有“回火”过程的降温函数来替代传统的指数降温函数,达到提高退火效率的目的,但其本质还是指数降温,不具有记忆功能,没有将两个过程的结果进行比较,所以该算法有可能遗失最优解;朱颢东等(2009)、周杰明等(2010)提出了带记忆的模拟退火算法思想,引进自适应温度更新函数,这种算法具有记忆功能和自适应性,但未给出具体的降温函数表达式,其可行性无从考鉴。本文在上述研究基础上,拟对模拟退火算法中的降温函数做进一步的改进。
1 改进的模拟退火算法
Metropolis等(1953)提出了Metropolis准则,即模拟退火算法的解是否被接受的判断准则。利用此准则编写的模拟退火算法大大减少了CPU时间,提高了最优解搜索效率。本文在陈华根等(2006)、孙海等(2014)研究基础上对降温函数作了进一步的改进,选取一种类似于多普勒效应型温度递减曲线表达式:
T=T0αk(cos(π/(2(1-k/K)))+
cos(π/(2T0(1-k/K)))
式中,k为迭代次数,K为总的降温次数。得出的曲线对比如图1。

图1 三种降温曲线图比较Fig.1 The comparisons of the three cooling curves
由图1可见,指数降温方式在迭代次数较少时,温度难以达到低温状态;快速降温方式则过早地降到了低温状态,使得后续的迭代求解无甚改变,基本已成定局。而中间的“多普勒”型曲线则很好地综合了二者的优点并消除了其缺陷,不但趋于低温的速度不紧不慢,而且在退火过程的后半部分还进行了不断地“回火升温”过程,使得算法在优化过程中具有多次跳出局部最优的机会,从而更容易地找出全局最优解。由于是多次降温的过程,故此算法增加了记忆功能,使得算法在降温过程中不会遗失最优解。改进的模拟退火算法步骤具体为:
Step 1 初始化:初始温度T0,终止温度Tf,初始解状态S,温度衰减参数α,以及每个T值的迭代次数L,记忆矩阵M;对温度T和k=1,2,…,L,做第2步至第5步工作;
Step 2 对初始解状态S,采用两点变换法、三点变换法以及两点逆序法交替使用的方式产生新解S′,计算增量Δt′=C(S′)-C(S),其中C(S)为评价函数;
Step 3 执行Metropolis准则:若Δt′<0则将S′接受为下一次产生新解的当前解,或者当Δt′>0时,若概率exp(-Δt′/T)>rand(1),也接受S′作为新的当前解,否则将当前解返回到上一次迭代时的当前解;
Step 4 执行记忆功能:若迭代次数为1,则将当前产生的最好解记录在记忆矩阵M之中;否则将当前产生的最好解与记忆矩阵M中的解进行比较,如果当前解优于记忆矩阵中的解,则将当前解写入记忆矩阵M中,否则保留记忆矩阵中的解;
Step 5 执行温度衰减函数:启用“多普勒”型衰减函数衰减T值,返回第2步继续寻优迭代过程,直到达到终止温度Tf时终止迭代;
Step 6 温度衰减完毕,返回最优目标函数值,结束程序。
2 数值实验
本文以TSP问题作为实验对象,用新的改进模拟退火算法重新对该问题进行试验,并将其与其他改进的模拟退火算法进行比较。
实验一 测试数据:CHN31,城市规模:31个。参数设置为:T0=100,L=10 000,α=0.99,Tf=0.6;
实验二 测试数据:TSPLIB中的att48,城市规模:48个。参数设置:T0=100,L=10 000,α=0.99,Tf=0.6;
实验三 测试数据:CHN144,城市规模:144个。参数设置:T0=100,L=10 000,α=0.99。
通过MATLAB 2015a测试得到相应的最优路径图如图2。

图2 三个数值实验结果Fig.2 The results of three numerical experiments
测试得到具体数据与文献对比结果如表1。
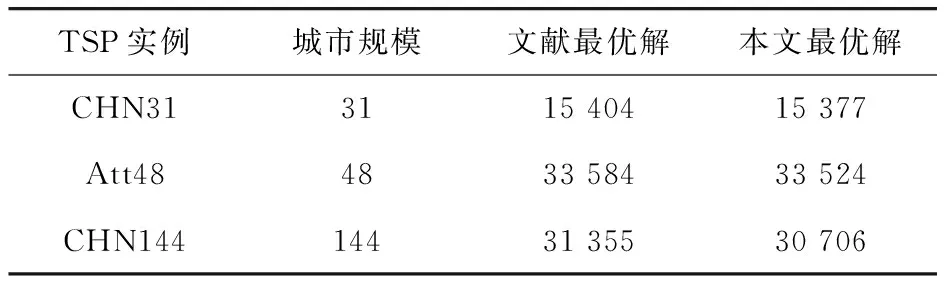
表1 改进的算法所得结果与当前文献对比表
注:对于CHN31、Att48实例中的文献最优解来自辛振铭(2010);CHN144实例中的文献最优解来自黄丽韶(2012)。
从表1试验结果得出,利用本文改进后的算法在求解的质量上都要高于文献中所利用的模拟退火算法,且改进后的算法在避免求解陷入局部极小值上有着很大的提高。这三组试验在matlab2015a仿真实验中证明了其收敛性,其结果是可靠的,说明改进后的算法应用于TSP问题中的正确性和可行性。
3 结束语
随着TSP问题在现实生活中慢慢凸显出的重要地位,对TSP问题求解性能要求的提高已经迫在眉睫,各种优化算法及改进方法需要经过TSP问题来不断验证其正确性和可行性。本文对模拟退火算法的降温策略进行了研究,提出了“多普勒”型降温曲线,理论上此种改进既能增加算法跳出局部最优的概率,一定程度上也提高了算法效率,使得算法在得到改进的同时并未增加实现的困难。
陈华根, 李丽华, 许惠平,等.2006. 改进的非常快速模拟退火算法[J]. 同济大学学报, 34(8):1121-1125.
黄丽韶.2012. 基于模拟退火算法的TSP研究[J].应用技术与研究, 4: 36-38.
孙海, 熊思灿, 吴志强, 2014. 基于改进SIR模型的甲型H1N1流感防控研究[J]. 东华理工大学学报:自然科学版,37(1):96-100.
吴进波, 熊盛武, 徐宁.2007. 温度可控的求解TSP问题的模拟退火算法[J]. 计算机应用研究, 24(5):66-67.
辛振铭.2010. 一种改进的模拟退火算法在TSP问题中的研究与应用[D]. 东北师范大学.
周杰明, 邓迎春, 黄娅.2010. 一种带记忆的模拟退火算法求解TSP问题[J]. 湖南文理学院学报, 22(2):70-73.
朱颢东, 钟勇.2009. 一种改进的模拟退火算法[J]. 计算机技术与发展, 19(6):32-35.
Metropolis N, Rosenbluth A W, Rosenbluth M N,et al. 1953. Equation of calculations by fast computing machines[J]. Journal of Chemical Physics, 21(4):1087-1092.
Modified Strategy of Cooling Based on Simulated Annealing Algorithm
NING De-sheng, ZENG Guang, LEI Li, XU Xi
(School of Sciences, East China University of Technology, Nanchang, JX 330013, China)
The cooling strategies of the algorithm is concerned. A kind of cooling curve which is similar to Doppler effect temperature decline curve is proposed. The memory function is increased, by which the defect of traditional simulated annealing algorithm easily falling into local minimum is avoided and the quality of searching global optimal solution is improved. With the experiment of TSP problem, the result shows that the strategy is superior to the conventional ones.
simulated annealing algorithm; cooling strategy; Doppler’s type; memory function
2015-10-31
国家自然基金(11661005,11301070);江西省自然基金(20132BAB211016;20151BAB211012);江西省教育厅科技项目(GJJ150576)
宁德圣(1992—),男,硕士研究生,主要从事数值算法设计与优化及矩阵计算研究。E-mail: 850640330@qq.com 通讯作者:曾 光(1984—),男,博士,副教授,主要从事高性能科学计算及应用研究。E-mail:zengguang5340@ecit.cn
10.3969/j.issn.1674-3504.2016.03.016
TP301.6
A
1674-3504(2016)03-0298-03

