非圆行星轮系瞬态动力学分析

张春鹏，李殿起，郭守存，尚志强

(沈阳工业大学，机械工程学院，辽宁 沈阳110000)



非圆行星轮系瞬态动力学分析

张春鹏，李殿起，郭守存，尚志强

(沈阳工业大学，机械工程学院，辽宁 沈阳110000)

论文分析了非圆渐开线直齿轮传动的节曲线方程,利用三维软件对非圆行星轮系进行三维建模，再把模型导入Adams中进行运动学和动力学分析。对非圆齿轮行星轮系运动过程中的输入力矩、输出力矩的特性进行了研究，从而分析出非圆行星轮系在运动过程中轮齿受力最大的位置,再把模型导入Ansys/Workbench中进行瞬态动力学分析,以准确、快速地得到非圆齿轮行星轮系在啮合过程中轮齿表面的应力分布图以及总变形图，从而验证非圆行星轮系结构设计的正确性。为优化非圆行星轮系的结构设计及应用提供重要数据。

非圆齿轮行星轮系；Ansys；节曲线；瞬态动力学

0 前言

一种新型的低速大扭矩液压马达是由非圆行星齿轮机构与液压马达技术结合起来组成的。波兰人最早发明这种液压马达，其它部分国家相继对这种液压马达进行了研究，目前波兰、德国、美国等国家已经掌握了生产非圆齿轮液压马达的技术。这种新型的非圆行星齿轮式低速大扭矩液压马达具有结构紧凑、零件少、易于加工和装配，重量轻、结构简单、易于实现与其他设备配套，低速运转平稳，机械效率高，抗工作油污染能力强等优点，因此对非圆齿轮液压马达的研究很有意义。非圆齿轮行星轮系机构是液压马达的核心部件，本文主要针对波兰海德曼公司生产的4-6型液压马达中的非圆行星轮系机构，建立非圆齿轮行星轮系动力学模型并对其动力学特性进行研究。

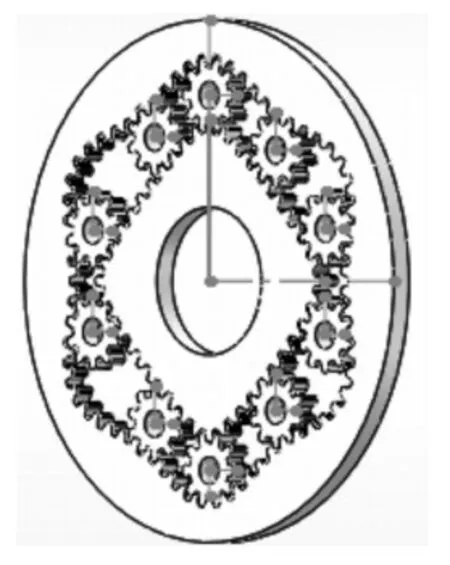
图1 非圆齿轮行星轮系Fig.1 Non-circular gear planetary gear train

1 非圆柱直齿轮传动的基本理论

(1)

图2 非圆齿轮传动简图Fig.2 Non-circular gear transmission diagram

2 非圆齿轮行星轮系的建模

本文采用了非圆行星轮系机构中内齿圈的节曲线是高阶椭圆，根据非圆柱直齿轮传动原理推导出太阳轮的节曲线方程，运用MATLAB对方程式编程并输出太阳轮和内齿圈的节曲线图形。非圆柱直齿轮的齿形是各不相同的，传动比是变化的，一般来说，非圆柱直齿轮的齿形不能用简单的解析函数来进行表达，而是通过齿轮啮合原理逐步推导出来。根据齿轮啮合原理推导出非圆柱直齿轮的齿廓方程，采用Solidwork进行三维建模，通过Solidwork和Adams、Ansys之间的无缝连接，实现了在Adams环境中的运动学、动力学分析和有限元环境中的瞬态动力学分析。

内齿圈是高阶椭圆的极坐标方程为

(2)

式中，是n1内齿圈的曲边数，Rz是中径，e是偏心率。

参照文献[1]相关公式计算出太阳轮的节曲线坐标，再通过Matlab画出如图3所示的节曲线。

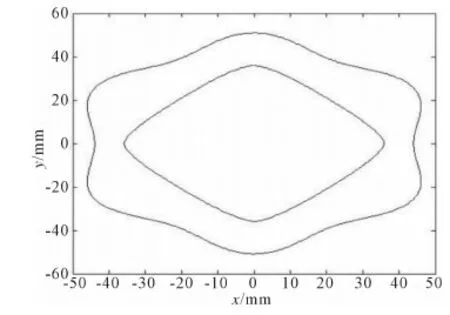
图3 太阳轮和内齿圈的节曲线Fig.3 Pitch curve of the sun gear and the internal gear ring

3 动力学运算方程

3.1 运动方程的建立

本文采用了拉格朗日乘子法建立系统运动方程为

(3)

完整约束方程时，f(q,t)=0

非完整约束方程时，g(q,q,t)=0

式中，T为系统动能；Q为系统广义坐标列阵；p为对应于完整约束的拉氏乘子列阵；M为对应于非完整约束的拉氏乘子列阵；q为系统广义速度列阵。

动力学问题遵循的平衡方程为

[M]{x″}+[C]{x′}+[K]{x}={F(t)]

(4)

式中，[M]为质量矩阵；[C]为阻尼矩阵；[K] 为刚度矩阵；{x}为位移矢量；{F(t)} 为力矢量；{x′}为速度矢量；{x″}为加速度矢量。

瞬态动力学分析是时域分析，是分析结构在随时间任意变化的载荷作用下的响应，动力响应过程的技术。其输入数据是作为时间函数的载荷，而输出数据是应力、应变或其他输出量如随时间变化的位移等。

3.2 齿轮表面的接触应力

该类齿轮工作时理论上载荷是通过线接触传递的，考虑到接触处的弹性变形，实际上就是小的面接触，根据Hertz理论，齿轮接触时产生的最大接触应力为

(5)

式中，F为齿轮副的法向压力；B为接触线长度；Δρ为接触点综合曲率；μ1、μ2分别为两齿轮材料的泊松比；E1、E2分别为两齿轮材料的弹性模量。

3.3 参数设置

该非圆行星轮系相关参数见表1。

表1 非圆行星轮系相关参数

4 Adams运动学仿真和Ansys瞬态动力学分析

4.1 齿轮材料的选取和设置

由于齿轮材料必须满足工作条件的要求，考虑到非圆齿轮液压马达在工作中受到的油压载荷冲击特殊的工况，该非圆齿轮液压马达选用硬度和韧性综合性能好的优质碳素结构钢，设置非圆齿轮行星轮系材料为45号钢。

4.2 Adams仿真分析

仿真的过程中，一方面是由模型的组装、添加约束时所造成的干涉、过约束等原因导致仿真结果的不收敛，导致仿真失败；另一方面是仿真参数的设置会影响仿真结果。在非圆齿轮行星轮系几何模型的基础上对非圆齿轮行星轮系的各个零件添加物理属性包括系统部件的泊松比、材料密度和弹性模量。设置所有部件的重力，确定部件间的约束关系，把内齿圈固定在大地上面，太阳轮与大地构成一个旋转副，行星轮分别与太阳轮、内齿圈设置为共面约束，在主动轮输入一个恒定的角速度，时间为0.1s，步长为0.001，在仿真之前对模型进行检验。可以对系统的构成、系统的自由度、未定义质量的构件和过约束等进行查询。在进行动力学仿真之前进行静态分析，以避免样机在启动时出现的一些瞬态响应导致仿真无法进行。

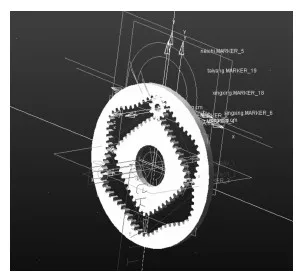
图4 约束后的Adams模型Fig.4 Adams model after constraint

在实际的液压马达应用当中，太阳轮的输出力矩不能有太大的波动，本文采用逆向思维，给定太阳轮一个恒定的角速度来反求主动轮行星轮在绕着太阳轮旋转一周运行过程中所受的力。

求解齿轮副在Adams动力学模型下承受力矩下的响应，其中行星轮上承受的受力变化曲线图和力矩变化曲线。

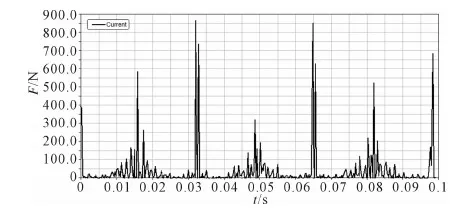
图5 行星轮受力图Fig.5 Force diagrams of planetary wheel

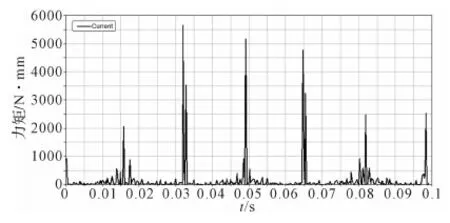
图6 行星轮所受力矩图Fig.6 Torque diagrams of planetary wheel

图7 行星轮质心角速度Fig.7 Angular velocity of planets wheel mass centre

由Adams分析可知非圆齿轮行星轮系传动过程中轮齿受力最大的位置出现在太阳轮、内齿圈极径最大处。

4.3 Ansys/Workbench分析

4.3.1 划分网格和接触设置

设置网格划分方式和网格形式。在Workbench环境下对非圆行星齿轮系模型采用结构化网格进行单元划分，为提高有限元分析的计算精度对齿轮的二维模型进行网格划分，并把模型划分为非接触区域和接触区域两部分。由于非圆行星轮系在运行的过程中的轮齿之间相互接触的面太多，容易导致计算不收敛，所以对接触面的有限元网格进行局部细化，从而得到更为精确的数值求解和加速求解的收敛。

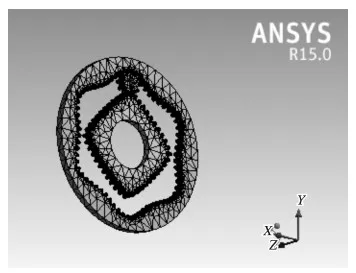
图8 有限元网格模型Fig.8 Finite element mesh model

4.3.2 施加载荷和约束

添加运动副和约束。设置太阳轮为转动副，内齿圈为固定副，约束太阳轮表面节点的轴向和径向位移，只保留Z轴方向上的转动自由度。约束行星轮在Z轴方向上的位移，行星轮除绕自身轴线自传外，还绕太阳轮公转，内齿圈加固定约束；分别设置行星轮与太阳轮、内齿圈的接触为自动的面与面的接触，实际上齿轮传动是线接触的，在每个齿的两面都定义接触，接触类型的选择为Frictionless，通过定义接触对可以确保轮齿在啮合时接触部分的变形和受力能够被随时定位和追踪。求解时间为0.1s，步长为0.001。在运动副里面给太阳轮施加一个旋转载荷。

当行星轮运行在太阳轮和内齿圈极径最大处时，行星轮系的分析结果如图9所示。

当行星轮运行在太阳轮和内齿圈极径的一般位置时，行星轮系的分析结果如图10所示。

图9 应力应变图Fig.9 Stress-stain diagram of planetary gear train

由上图可知当行星轮处于太阳轮和内齿圈极径最大处时受力和变形最大，与Adams分析的结果一致。齿轮的失效主要发生在轮齿根部和轮齿表面上，从非圆行星轮系的等效应力分布图上可以看出，在轮齿运转过程中，太阳轮受力比较大，容易损坏，太阳轮在极径最大的位置时受力最大，所以只需校核太阳轮极径最大位置时的强度。但是太阳轮与行星齿轮所受最大等效应力大致相等，应力比较大的地方主要集中在齿根附近和啮合轮齿接触处。在两个啮合轮齿的轮齿根部及齿廓曲面上出现齿轮的最大应力，随着非圆行星轮系的运转，轮齿的最大应力呈现周期性变化。最大剪切应力为258MPa，最大等效应力为325MPa，都小于齿轮的许用应力，在齿廓表面和齿根处未出现较明显的应力集中现象，应力分布也较为均匀。而且应力影响区域在接触齿对几个齿附近，远离接触区域处的应力为零，完全符合弹性力学中的相关定律。

图10 应力应变图Fig.10 Stress-stain diagram of planetary gear train

5 结束语

(1)由行星轮的受力图可以看出行星轮受力的最大的位置出现在太阳轮和内齿圈极径最大值处，为非圆齿轮行星轮系材料的强度校核提供有效的数据。从而判断各零件的强度是否达标，结构是否正确。

(2)有限元和虚拟样机技术的应用为有效的解决实际应用问题提供了便捷途径，方便、快捷地利用静力学仿真数据对行星轮系施加动态载荷，进行运动仿真和动态动力学仿真。得到动态载荷下轮系上各个齿轮的应力分布云图、等效弹性应变和总变形图，从而为机构的优化设计提供了一定的依据。

[1] 姚文席.非圆齿轮设计[M].北京:机械工业出版社,2012.

[2] 贾长治,股军辉,薛文星.MDADAMS虚拟样机从入门到精通[M].北京：机械工业出版社,2010.

[3] 连锦程.基于ADAMS的齿轮传动特性仿真分析[J].制造业自动化，2011(12):148-150.

[4] 杨生华.齿轮接触有限元分析[J].计算力学学报,2003,20(2):180-194.

[5] 李军,覃文洁.ADAMS实例教程邢俊文[M].北京：北京理工大学出版社，2002.

[6] 陈文华,贺青川,张旦闻.ADAMS2007机械设计与分析范例[M].北京:机械工业出版社,2009.

[7] 黄志新,刘成柱.ANSYS/Workbench14.0超级学习手册[M].北京:人民邮电出版社,2013.

[8] 陈岚.基于ANSYS/LS-DYNA的行星轮系传动系统瞬态动力学分析[J].河南科技,2013(17):222-223.

Transient dynamics analysis of non-circular planetary gear train

ZHANG Chun-peng， LI Dian-qi，GUO Shou-cun，SHANG Zhi-qiang

(School of Mechanical, Shenyang University of Technology, Shenyang 110000，China)

The paper analyses pitch curve equation of the non-circular involute spur gear transmission, 3 D model of the non-circular planetary gear train is build by using 3 D software, and then put the model into Adams for kinematics and dynamics analysis. The input and output torque characteristics of the non-circular gear planetary gear train is studied, so as to analyze the largest stress position of gear tooth during movement. And then put the model into Ansys/Workbench for transient dynamics analysis, stress distribution and total deformation of the tooth surface are accurately and quickly get in meshing process. The results show the structure design of non-circular planetary gear train is accurate. It also provides reference data for optimizing the structure design and the application of the non-circular planetary gear train.

non-circular gear planetary gear train; Ansys; pitch curve; transient dynamics

2015-09-26；

2015-12-23

国家自然科学基金项目(No.51105257, No.51310105025)

张春鹏(1991-)，男，沈阳工业大学硕士研究生。

TH132.424

A

1001-196X(2016)05-0076-05