纺织学科期刊h指数、总被引频次和影响因子之间的相关性研究

李启正，徐石勇，杨一舟

(浙江理工大学《丝绸》杂志社，杭州 310018)



纺织学科期刊h指数、总被引频次和影响因子之间的相关性研究

李启正，徐石勇，杨一舟

(浙江理工大学《丝绸》杂志社，杭州 310018)

为研究同学科期刊主要引证指标之间存在的相关关系，以《中国科技期刊引证报告(扩刊版)》统计的30种纺织学科期刊为研究对象，采用SPSS和Origin对它们的h指数、总被引频次和影响因子进行相关性和拟合分析。研究发现：期刊的h指数、总被引频次和影响因子三者之间两两均成较高程度的正相关关系(Pearson等级相关系数介于0.835～0.902，P<0.01)；在进行拟合分析时，如将学科中的高自引和内容性质变化期刊排除，它们之间的相关程度进一步提高。正常出版期刊的影响因子和h指数之间具有较好的线性关系(R=0.94)，但总被引频次/h指数，总被引频次/影响因子之间更符合二次拟合关系(R分别为0.97和0.98)。导致相关异常的期刊往往存在高自引、期刊内容性质变化等情况。

h指数；总被引频次；影响因子；相关性；纺织期刊

目前用于评价科技期刊影响力的主要指标为“影响因子”。但单一的引证指标或体系已不能全面、准确地评价科技期刊的质量。随着新的统计手段和计量方法的不断发展和应用，开发出了不同的引证指标和体系，可以从不同角度反映期刊的学术影响力。在同一学科内，某些期刊在某些引证指标上存在明显的缺陷或异常，则可反映出该期刊在综合水平上的不足[1-2]。近来，新的期刊评价指标“h指数”受到业内极大关注，并已逐渐成为期刊评价的重要指标之一[3]。关于“h指数”“总被引频次”和“影响因子”的相关性分析，目前也有不少的研究。现有研究表明，期刊h指数、影响因子和总被引频次之间有着较强的相关性，但不同学科类型期刊样本之间的相关程度存在一定的差异，见表1。

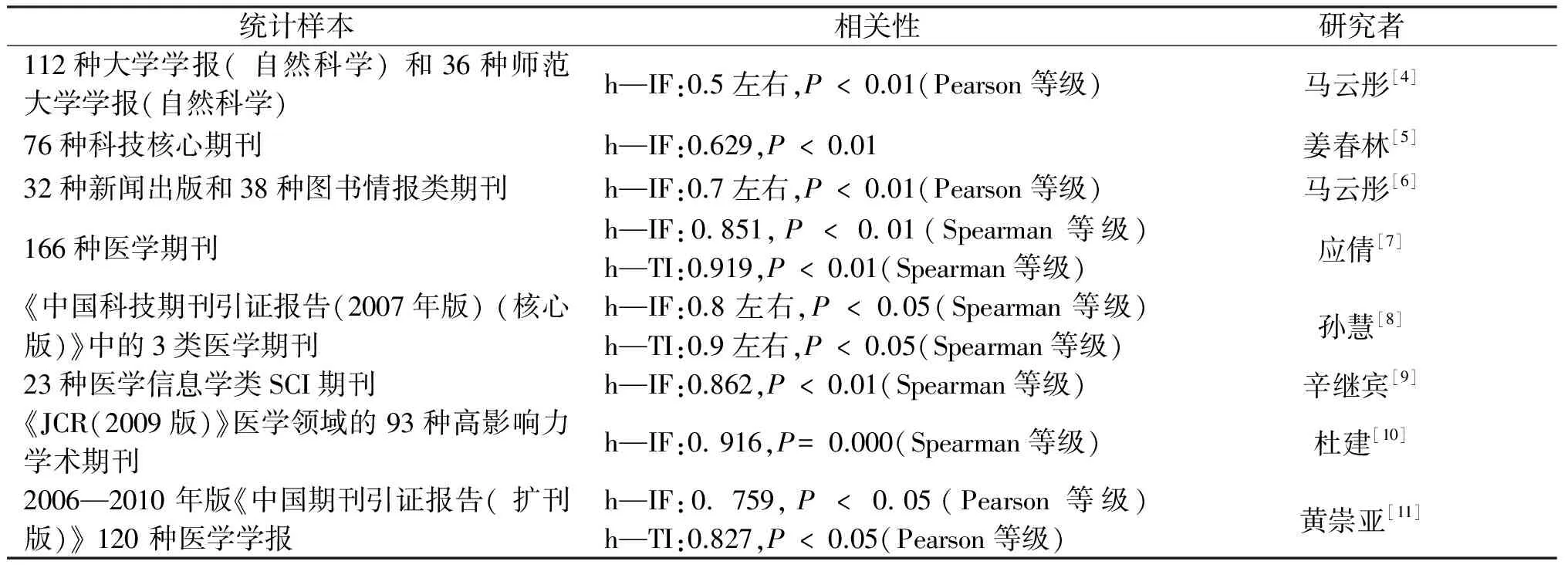
表1 不同学科类型期刊样本之间引证指标的相关性

注：h—IF表示h指数和影响因子之间的相关关系，h—TI表示h指数和总被引频次之间的相关关系。

从已有文献的报道中可以发现：不同领域和不同类型期刊样本中，期刊h指数和影响因子的相关程度均呈显著相关，但相关程度按照大学学报类自科期刊、科技类核心期刊、情报学等普通领域期刊、医学领域期刊、SCI期刊和高学术影响力期刊依次递增，即学术影响力高的期刊样本和专业性强的期刊样本能够得到更高的相关系数；此外，“期刊h指数/总被引频次”的相关性较“期刊h指数/影响因子”的相关性更强。目前，对全体纺织学科期刊引证指标之间的相关性研究还未见报道[12]。本文以2013年版《中国科技期刊引证报告(扩刊版)》统计的30种纺织科技期刊为研究对象，研究期刊h指数、总被引频次和影响因子之间的相关性，并通过拟合，分析其相关系数的变化规律。本研究不仅可以了解纺织学科期刊发展的整体状况，发现学科内的异常期刊，提供新的视角和观点，还可为更客观、合理地应用不同评价指标来评价科技期刊提供参考。

一、数据来源及研究方法

(一)数据收集

纺织学科属于工程技术领域，一般地可细分为纺织工程、纺织材料、纺织品设计与纺织化学和染整工程等二级学科，主要研究如何用物理、化学、机械等高科技手段实现和满足各领域和各种功能要求的纺织品的加工和评价。与医学、生物学等新兴学科相比，纺织学科期刊具有期刊品种数偏少，篇均参考文献数量偏少，整体影响因子偏低，文章内容应用性、技术性较强，论文时效性不显著，引用年限长等特点。

由于《中国期刊引证报告(扩刊版)》2015年版不再划分期刊学科，2014年版引证报告部分期刊统计数据不全，本文以2013年版《中国期刊引证报告(扩刊版)》统计的30种纺织学科期刊为研究对象，如表2所示。其中《纺织标准与质量》和《检验检疫学刊》由于缺少统计数据，不列入研究对象。由于《中国期刊引证报告(扩刊版)》各年划分的纺织学科期刊不完全相同，且部分期刊存在个别年度数据缺失等情况，同时为使统计数据更真实客观，研究选取2011—2015年版(2010—2014年)5年的总被引频次、影响因子、他引率、载文量等指标平均后进行分析。期刊h指数系笔者自己统计获得，其检索方式为CNKI中国引文数据库的精确检索，数据检索时间为2016年6月15日。

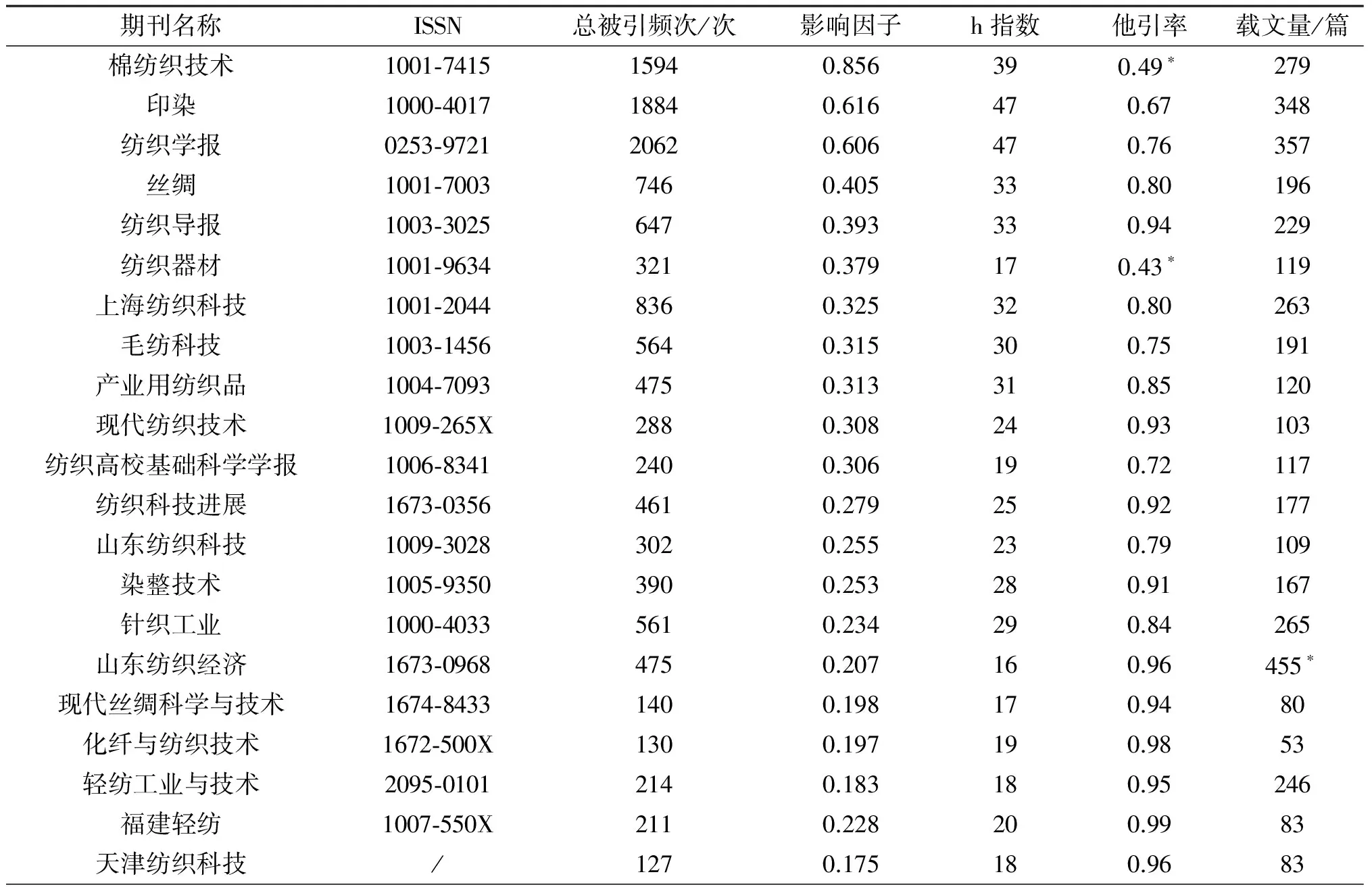
表2 近5年纺织学科科技期刊主要指标统计

表2续

注1：标注*的数据为明显异常数据。

注2：总被引频次、影响因子、他引率、载文量均为2010—2014年的平均值；《非织造布》2014年起停刊，《纺织科学研究》《中国纺织》《江苏丝绸》《江苏纺织》《纺织机械》等近年期刊内容性质发生较大变化，2014和2015版《中国期刊引证报告(扩刊版)》开始不再统计它们的引证指标，本文仅对其近5年有指标的年份进行平均。

(二)研究方法

采用SPSS V20统计软件，对30种纺织期刊的总被引频次、影响因子和h指数进行相关性分析。首先采用Kolmogorov-Smirnov Test (K-S检验) 对样本数据进行正态性检验(表3)，发现3组样本数据的Sig.都大于0.05，均符合正态分布。满足线性假设的正态分布连续数据可采用Pearson相关系数进行分析。数据拟合采用Origin数据分析软件，拟合方法为线性拟合和二次拟合。

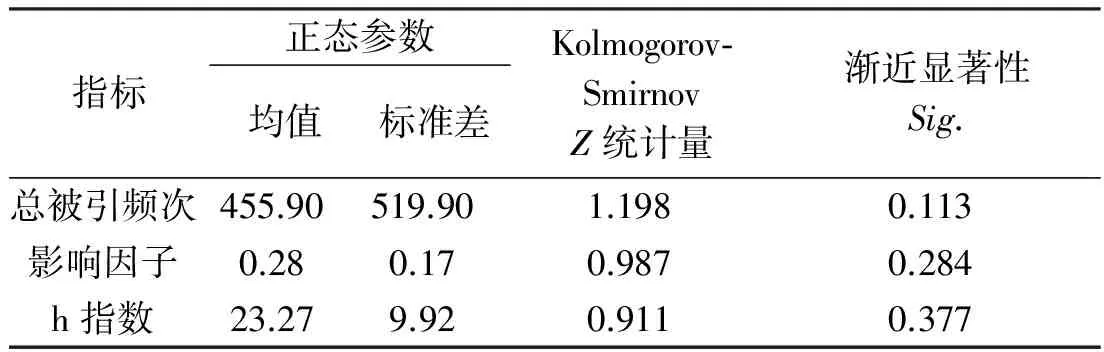
表3 主要引证指标的正态性检验

注：Sig.大于0.05，检验分布为正态分布。

二、分析与讨论

(一)自引对Pearson等级相关系数的影响

为研究纺织学科期刊各主要引证指标之间的相关程度，在SPSS中将30种纺织期刊的h指数、总被引频次和影响因子进行相关性分析。分析结果如表4所示。

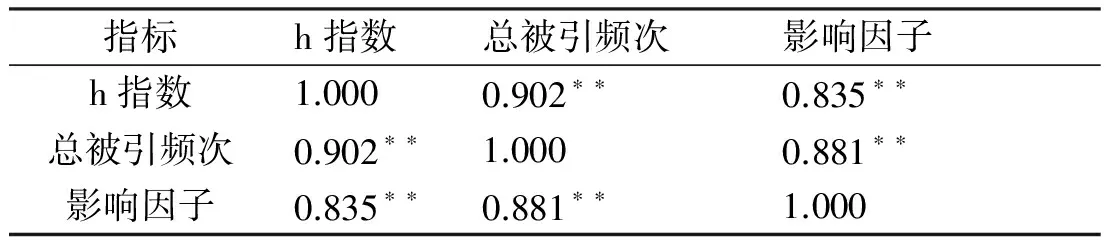
表4 纺织学科期刊主要引证指标之间的Pearson等级相关系数

注：**表示在置信度(双测)为 0.01 时，相关性显著。

在0.01置信度(双测)上，h指数、总被引频次与影响因子三者两两之间Pearson等级相关系数均在0.835以上，相关显著。其中，期刊的h指数与总被引频次之间的相关性最好，Pearson等级相关系数为0.902。从表1的数据中可以发现，30种纺织期刊的平均他引率为0.87，其中有2种期刊的他引率大大低于正常水平，分别是ISSN 1001-7415的0.49和ISSN 1001-9634的0.43。为避免高自引期刊对整体相关规律的影响，排除该两种期刊，再进行相关性分析。分析结果如表5所示，在0.01置信度(双测)上，h指数、总被引频次与影响因子三者两两之间相关显著性更加强烈，与影响因子有关的等级相关系数有明显的提高。

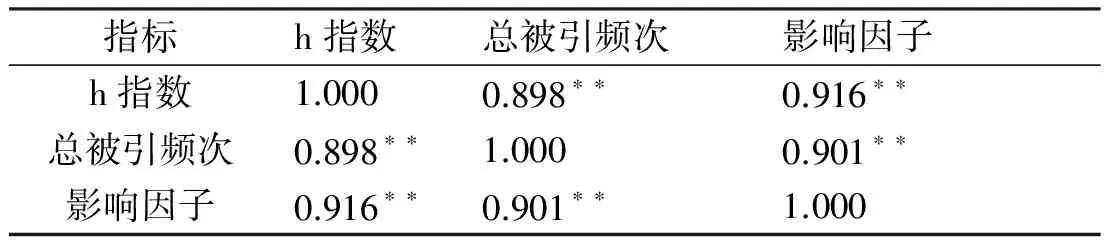
表5 排除高自引期刊后纺织学科期刊主要引证指标之间的Pearson等级相关系数

注：**表示在置信度(双测)为 0.01 时，相关性显著。

分析上述变化的产生原因，可能是h指数、总被引频次和影响因子都属于期刊的被引用指标，它们都是因为期刊登载的论文被引用而产生数值，它们之间本身便具有很强的关联性。但h指数和总被引频次主要与期刊论文被引的长期积累相关密切，而影响因子一般统计最新两年的数据，因此，自引对它们的影响不如对影响因子的影响明显。由此可见表4的相关系数中，与影响因子有关的等级相关系数都相对低一些。期刊h指数的定义为某期刊发表的所有文章中有h篇论文至少被引用了h次。如个别期刊增加的自引(或引用)不在使其h指数上升的相关文章上，即不符合期刊h指数的增长规律，对h指数甚至不会产生影响；而影响因子统计的是某期刊在统计年前两年发表论文在统计当年被引用的次数除以该刊前两年发表论文的总数。影响因子设置了引用时间限制，又受载文量的影响，与期刊的长期积累的数据关系不密切，是一个较为动态的引证指标。期刊增加的自引在统计年前两年被引数据时可以快速、明显地提高影响因子，对期刊评价的影响较大。

因此，在本研究的相关性分析中，当将学科中过度自引的期刊从分析中排除后，学科整体影响因子分布恢复正常水平，与影响因子有关的相关性系数也得以提高。但h指数和总被引频次对自引不敏感的原因还需要在拟合坐标中进行具体分析。

(二)相关异常的拟合分析

1.影响因子与h指数相关分析

将30种纺织期刊的h指数和影响因子分布情况通过Origin绘制在坐标图中。如图1所示，其分布呈现一定的规律性，即影响因子越高的期刊，h指数一般也比较高。通过对这些散点数据进行线性拟合后发现，有3个期刊明显偏离了拟合线，使得拟合线的线性相关系数只有0.84，其中1001-7415和1001-9634为本学科他引率最低的两种期刊，ISSN 0529-6013为期刊内容性质发生重大变化的期刊：其2010年载文量为35篇，影响因子为0.472，尚属正常学术期刊。但2011年和2012年其载文量大幅上升到344和934，影响因子却急剧下降到2012年的0.063，2014版和2015版《中国期刊引证报告(扩刊版)》已不再统计该刊。将3个异常期刊从分析中排除后，拟合线的拟合度得以大大提高。如图2所示，大部分期刊均分布在拟合线上或拟合线附近，线性拟合相关系数也提高到0.94。

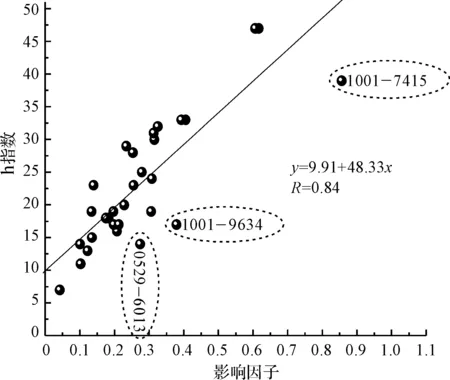
图1 h指数与影响因子的拟合关系

因为影响因子与统计时间窗关系密切，而h指数更注重历史积累。1001-7415和1001-9634远离拟合线的原因可能是期刊的部分自引带动了影响因子的提高，但未带动h指数的同步提高，说明期刊h指数受自引的影响较影响因子小。

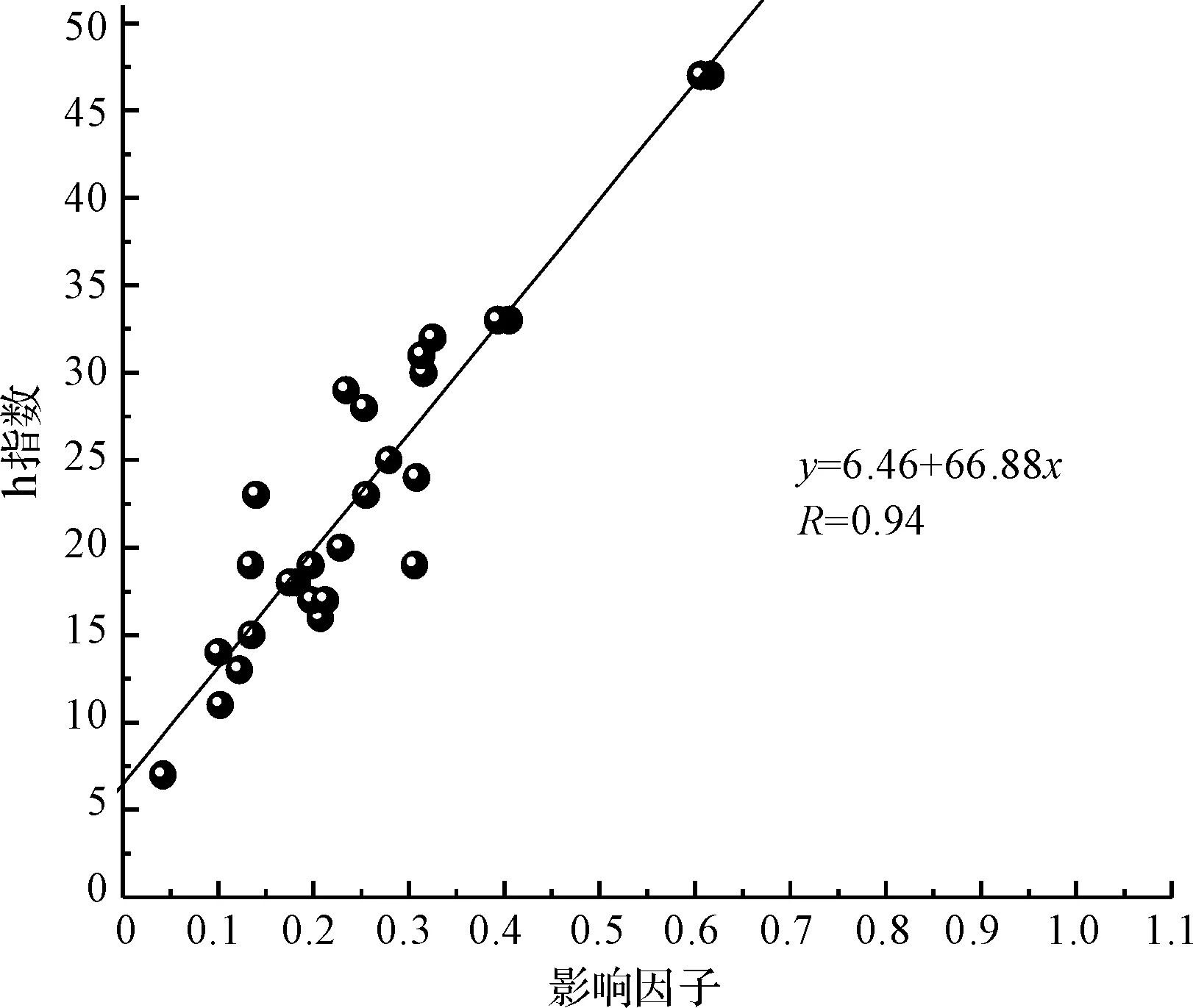
图2 排除异常期刊后h指数与影响因子的拟合关系

2.总被引频次和影响因子相关分析

同样，将30种纺织期刊的总被引频次和影响因子分布情况绘制在坐标图中。如图3所示，其分布呈现较好的规律性，即影响因子越高的期刊，总被引频次一般也比较高。它们的线性拟合相关系数为0.88。同样，1001-7415和1001-9634两个他引率最低的期刊以及0529-6013内容性质发生重大变化期刊与整体规律偏离较大，排除它们后进行重新拟合。如图4所示，总被引频次和影响因子的分布情况可以用相关系数为0.91的直线进行拟合，还可以用相关系数为0.97的二次曲线进行拟合。由图4可知，期刊影响因子与总被引频次之间的关系更符合二次分布，即期刊的影响因子达到一定程度后，总被引频次的增加对影响因子的影响越来越小。

图3 总被引频次与影响因子的拟合关系

图4 排除异常期刊后总被引频次与影响因子的拟合关系

3.总被引频次和h指数相关分析

将30种纺织期刊的h指数和总被引频次分布情况绘制在坐标图中，可以发现其分布亦呈现出较好的规律性。如图5所示，其线性拟合相关系数为0.90，二次拟合系数为0.93。两种他引最低期刊的坐标虽没有落在“h指数/总被引频次”拟合线上，但并没有远离拟合线，相比较纺织学科期刊的平均水平，两个他引最低期刊在总被引频次上比正常水平稍高。即期刊增加自引在一定程度上能够提高期刊的总被引频次，但对h指数的影响较小。同样，将两个自引较高的期刊排除，再对数据进行拟合分析，可以发现：新的拟合方程相关系数变化很小。研究认为，两个自引较高的期刊并未明显影响学科整体h指数与总被引频次的拟合关系。

图5 h指数/总被引频次的拟合关系

为进一步分析纺织学科期刊“h指数/总被引频次”的相关异常情况，将分布不符合拟合规律的3种主要期刊进行了标注，发现它们的出现也存在一定的规律性。从拟合分析中可以发现，1003-1308因为总被引频次(88次)大大低于学科平均值(456次)而远离拟合线，1003-9910因为h指数(7)和总被引频次(45次)都大大低于学科平均水平而远离拟合线。恰巧这两本期刊也是近年纺织期刊中转为行业新闻报道和行业资讯类型的期刊。2015版《中国科技期刊引证报告(扩刊版)》中不再收录1003-1308和1003-9910，2013版和2014版《中国科技期刊引证报告(扩刊版)》中统计它们的文献选出率均居本学科末位，也都证实了这两本期刊的转型情况。因此，研究认为行业资讯类期刊往往不符合期刊的“h指数/总被引频次”总体分布规律；1673-0968由于h指数远低于学科正常水平而远离拟合线，从表2可以发现，该期刊的引证指标在学科中处于中下水平，但平均载文量是学科中最高的，达到455篇，由于刊发的文章学术性偏低，有效引用偏低，导致h指数偏低。

图6 排除高自引期刊后h指数与总被引频次的拟合关系

图7为排除上述几种异常期刊后的数据分布和拟合分析，“h指数/总被引频次”呈现出较好的二次分布规律，拟合系数R达到0.98。在初始阶段，总被引频次与h指数呈现较好的线性正相关，但当h指数增加到一定数值后，总被引频次的增加比h指数的增加要快得多。

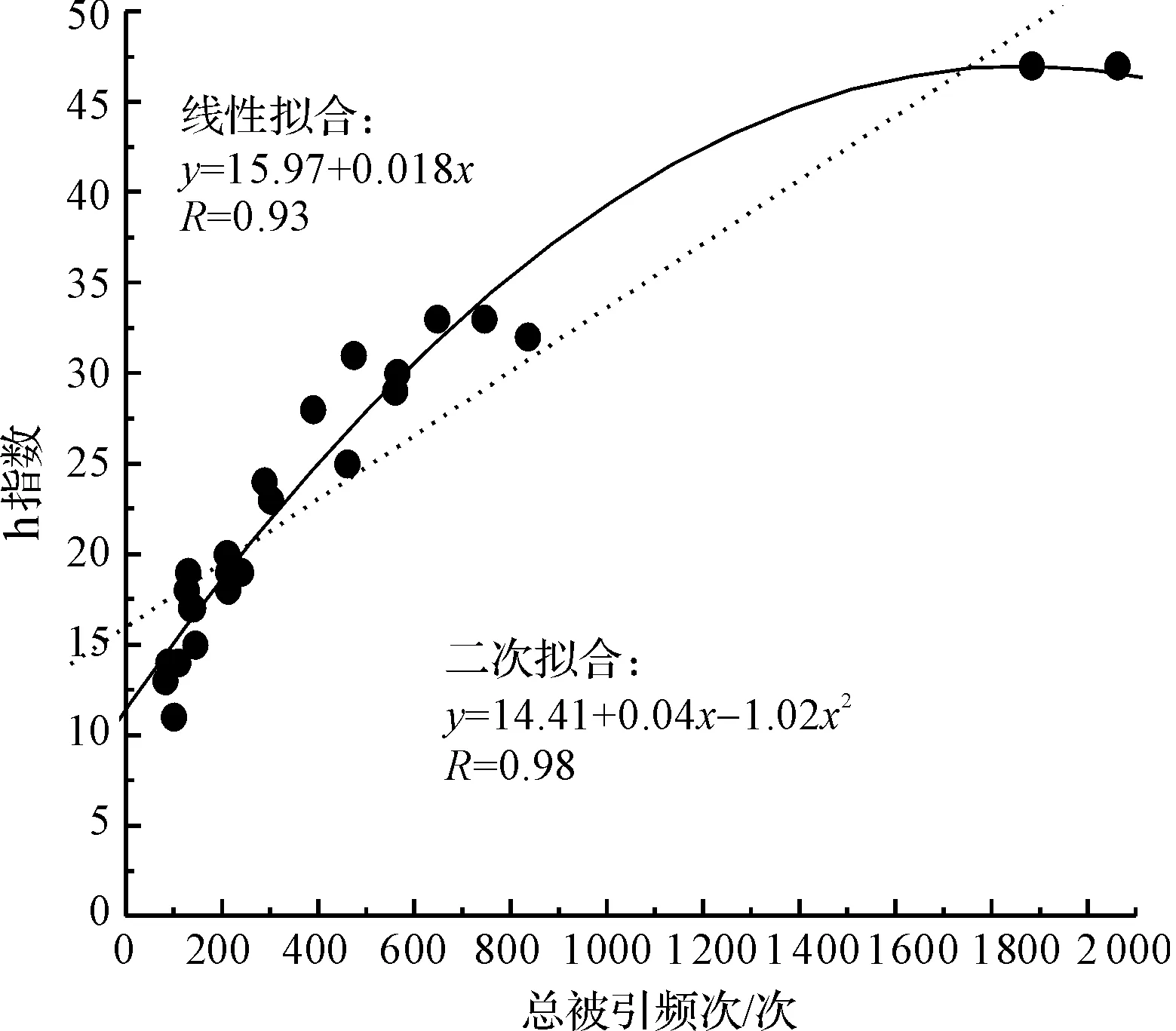
图7 排除相关异常期刊后纺织期刊h指数与总被引频次的拟合关系

(三)相关异常期刊对Pearson等级相关系数的影响

通过对学科内期刊引证指标的拟合分析，可发现相关异常的期刊。它们往往存在高自引、非学术型、非正常出版等异常行为。将上述异常期刊排除后，对剩余24种纺织期刊的h指数、5年总被引频次平均值和5年影响因子平均值进行相关性分析。分析结果如表6所示，在0.01置信度(双测)上，h指数、总被引频次与影响因子三者两两之间Pearson等级相关系数均超过0.922，显示出强烈的相关显著关系。

表6 纺织学科正常出版期刊主要引证指标之间的Pearson等级相关系数

注：**表示在置信度(双测)为 0.01 时，相关性显著。

三、结 论

h指数、总被引频次和影响因子等期刊引证指标可以从不同角度反映期刊的发展状况，通过对2011-2015年版《中国期刊引证报告(扩刊版)》收录的纺织学科期刊引证指标期刊h指数、总被引频次和影响因子的相关性和拟合分析，得到如下结论：

a)纺织学科期刊的h指数、总被引频次和影响因子之间存在显著相关关系，三个引证指标两两之间的Pearson等级相关系数均在0.835以上，P>0.01。排除异常期刊后，纺织学科期刊h指数、总被引频次和影响因子两两之间的Pearson等级相关系数可以达到0.922以上，P>0.01。

b)期刊高自引会造成期刊影响因子的较大变化，总被引频次的较小变化，h指数的微小变化甚至无变化。这种有层次的影响关系，反映在引证指标关系坐标中为数据点偏离正常拟合线。

c)通过对纺织学科期刊“h指数/总被引频次”的相关异常分析，可以发现本学科中高自引、非学术型、非正常出版等相关异常的期刊。可为研究本学科期刊的整体发展状况提供有效的参考。

[1] 梁霞,金顺爱,赵阳.传统期刊评价指标与h指数[J].编辑学报,2010(S2):165-168.

[2] GROESSER S N. Dynamics of journal impact factors[J]. Systems Research and Behavioral Science,2012,29:624-644.

[4] 马云彤.影响因子与h指数、复合影响因子相关性分析与回归拟合:以自然科学类大学学报和师范大学学报为样本[J].西安文理学院学报(自然科学版)2014,17(2):115-120.

[5] 姜春林.期刊h指数与影响因子之间关系的案例研究[J].科技进步与对策,2007,24(9):78-80.

[6] 马云彤.影响因子与h指数、复合影响因子相关性研究:以新闻出版和图书情报类期刊为样本[J].西安文理学院学报(自然科学版),2013,16(4):123-128.

[7] 应倩,夏庆民,戴丽琼,等.医学期刊h指数与影响因子总被引频次的相关性分析[J].中国科技期刊研究,2012，23(2):232-234.

[8] 孙慧,汤先忻.医学类期刊h指数与影响因子、总被引频次的相关性研究[J].中国科技期刊研究,2009,20(3):469-471.

[9] 辛继宾.期刊H指数与影响因子的关系研究[J].图书情报工作,2011(S1):270-271.

[10] 杜建,张玢,刘晓婷.期刊影响因子、h指数、相对h指数及特征因子的相关性分析[J].情报杂志,2011,30(2):23-28.

[11] 黄崇亚.我国医学类学报q2指数与h指数,m指数,影响因子,总被引频次的相关性研究[J].中国科技期刊研究,2012,23(6):979-981.

[12] 王金秀,潘黎明.纺织科学与工程核心期刊被引频次及影响因子研究[J].武汉纺织大学学报,2011(5):80-81.

(责任编辑：任中峰)

Research on Correlation Among H Index, Total Citations and Impact Factor of Textile Science Journals

LIQizheng，XUShiyong,YANGYizhou

(Journal of Silk, Zhejiang Sci-Tech University, Hangzhou 310018, China)

In order to study the correlation of major citation indexes of one type of journals, this study chose the 30 textile science journals included in Chinese S&T Journal Citation Reports (Expanded Edition) as research objects, and used SPSS and Origin to analyze the correlation and fitted relation among h index, total citations and impact factor. The research shows that every two indexes of h index, total citations and impact factor present a high degree of positive correlation (Pearson correlation coefficient is 0.835～0.902,P<0.01); if higher self-cited and contents-properties changed journals are excluded during fitting analysis, the correlation degree between them will further improve. The impact factor of normally published journals has a good linear relationship with h index (R=0.94), but the relationship of “h index/total citations” and “impact factor/total citations” is more aligned with the quadratic fitting formula, with correlation coefficientRof 0.97 and 0.98 respectively. The journals resulting in abnormal correlation often have high-self-cited rate or changed its properties of publication.

h index; total citations; impact factor; correlation; textile journal

10.3969/j.issn.1673-3851.2016.12.007

2015-06-17

浙江省科学技术协会精品科技期刊培育工程(KX20131102)

李启正(1981-)，男，浙江缙云人，博士，编辑，主要从事期刊出版方面的研究。

G255.2

A

1673- 3851 (2016) 06- 0547- 07 引用页码： 120302