我国白银期货最优套期保值比率的分析

陈玉秋

我国白银期货最优套期保值比率的分析

陈玉秋

文章主要研究我国白银的套期保值比率。首先讲述了对白银期货套期保值比率研究的内容和意义；接着对期现货价格数据进行处理，得到一段连续的数据，用最小二乘法来计算最优套期保值比率,然后对模型进行改进以及W hite检验。最后将套期保值有效性的度量指标与最小二乘法的拟合系数对应起来。

棉花期货；最优套期保值比率；最小二乘法；W hite检验

一、引言

期货不是货物，而是我们在买卖时进行交易的一种标的物，我们在现在时刻买卖标的物，但是在将来进行交收或交割，这个标的物可以是某种商品，也可以是金融工具。我们所约定的在将来进行交割的时间，可以定为一星期以后，也可以是一个月以后，甚至三个月以后，一年以后。期货的交割有一定的时间限制，在时间到期以前，期货是合同交易，到了到期日以后，就必须兑现合同，进行现货交割。白银期货作为新上市的期货品种，它的产生不仅丰富了我国的期货品种，也对白银生产和加工企业规避白银价格剧烈波动风险提供了一个渠道和价格指导。

（一）研究背景与意义

我国白银上市时间短，白银期货也是新的期货品种，随着时间的推移，我国的白银期货机制逐渐成熟。但是相对于国际白银市场相比还是有很多不足，还有待完善。中国作为白银的消费大国，其价格变动将对我国的白银产业链造成较大的影响。我们可以研究白银期货的套期保值来规避白银交易中的风险。所以把白银的套期保值作为控制风险的重要手段显得极为迫切，其中最为核心的问题就是如何估算套期保值比率来最大限度减小基差风险。所以研究白银的套期保值有着重要意义。

（二）套期保值简介

套期保值，主要是指我们采用一种套期工具来规避风险，这套工具的基本特征在于利用现货和期货的关系，在他们之间建立对冲机制，利用在现货或期货市场上盈利或亏损来弥补在期货或现货市场上的亏损或盈利，从而使风险降到最低。

二、研究方法和数据说明

该篇文章主要使计算白银的套期保值比率，主要用到最小二乘法，来对白银期货市场进行定性、定量的研究。我们主要从同花顺中上海期货交易所和中国商品交易网中获取中国白银期现货价格数据。本文所采用的一些数据主要是算数平均值，这些算数平均值是按照相应的期限对日收盘价数据计算得出的。此外，为了获取与现货和期货相配合的数据，我们对一些数据进行了剔除，比如那些只有期货数据没有现货数据，或者只有现货数据而没有期货数据的不匹配数据。

（一）普通最小二乘法

假设现在有一套期者要进行套期保值，利用现货和期货之间的对冲机制，在现货和期货之间进行交易，并把在两者之间的交易当做一个投资组合进行分析从而得到的该期间的收益为下式：

假定P1、F1、Qs、Qf已知，而P2、F2未知，收益Rh随着P2、F2的变化而变化。预期收益Rh我们用E（Rh）表示，而风险用Rh的方差Var（Rh）表示：

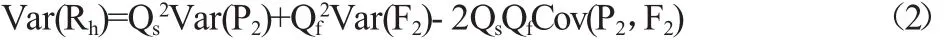
（2）式两边同时对Qf求导，即可得到方差Var(Rh)的最小值：

若令hmr=Qf/Qs，即为风险最小时的套期比，则有：

如果我们能够根据已经获得的数据估计Cov(P2，F2)和Var (F2)，那么就可得出套期保值的最小风险套期保值比hmr，如果Cov(P2，F2)＞0,则hmr＞0，它表示期货市场与现货市场盈亏相反，否则相同。然而一般情况下，P2、F2变化方向基本一致，所以一般hmr＞0。若套期保值者在该段期间内没有进行相应的套期保值，那么其收益就应该为下式：

其方差为:

令He=1-Var(Rh)/Var(Ru)

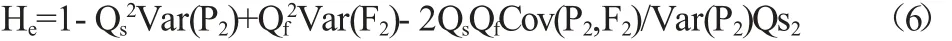
其中，He表示我们进行套期保值的风险规避程度，即进行套期保值相对于不进行套期保值交易的一种风险回避程度，因此我们也把它称作为套期有效性指标。

将hmr=Qf/Qs=Cov(P2,F2)/Var(F2)代入，此时方差最小，套期保值有效性指标为：

我们当前在利用最小方差进行套期保值时，一切都较理想化，而忽略了套期成本费用等因素。如果我们在进行套期保值时，如果加入套期成本费用等因素，那么利用最小二乘法计算的套期保值策略就会发生很大的变化。我们不妨设套期费用为：

Qs是指套期者在现货市场上进行商品交易的数量；Qf是指套期者在期货市场上进行商品交易的数量。而在（1）式中我们并没有考虑到交易成本，在开始套期时，P1、F1、Qs、Qf我们认为是确定的，而是P2、F2未知随机变量，收益Rh为随机变量，即随着P2、F2的变化而变化。Rh的预期收益我们用E(Rh)表示，而风险用Rh的方差Var(Rh)表示：

当Qf＜0时，表示买入期货合约Qf。

对于Qf＞0和Qf＜0,则（1）式分别变为：

式中C1表示固定费用，C1＞0;(F1+F2)QfC2表示套期保值风险随着成交额增加而增加，不管在现货或是期货市场上是买入还是卖出实货，也不管在现货或期货市场上是赚还是赔，1＞C2＞0。

同样以方差最小为准则：

（9）两边同时对Qf求导，得出：

于是可以得出，固定套期保值费用对方差最小套期保值比没有影响。

将（11）式代入（9）式得，方差最小时的套期保值有效性指标为：

所以我们可以得出当套期费用是(F1+F2)Qf线性函数时，我们可以得出式（12）表明套期有效性与交易费用无关。

因此根据套期保值有效性指标可以得出：

（1）Hec*＞0，说明在套期保值中期货价格与现货价格波动方向一致，那么我们为了规避风险，可以利用在期货市场和现货市场上进行反向套期保值。

（2）Hec*＜0，说明在套期保值中期货价格与现货价格波动方向不一致，那么我们为了规避风险，可以利用在期货市场和现货市场上进行同方向套期保值。

（3）从上述结论中可以发现，套期保值有效性指标可以很好地检测套期保值的有效性。

（4）我们对套期保值的有效性进行研究，首先要引入一个加了白银期货的套期保值投资组合的组合收益率，我们定义其为：Pt=St-βt*St，其中，Pt代表组合的收益率；St表示单位白银净值的收益率；Ft是白银期货的收益率，βt是根据不同模型所计算出的套期保值比例。

（5）St是白银单位净值的自然对数，Ft为白银期货价格的自然对数，而△St和△Ft分别为两种资产在时刻t所提供的实际收益率。于是我们就可以来估计单期的常数最优套期保值比率，我们通过下列回归模型来进行计算：

其中，α为常数项，εt为普通最小二乘回归模型的残差项；根据最小二乘法则，β的估计量为：

通过对上式进行最小二乘回归，就可以得到最小二乘回归的最优套期保值比率。由于任何期货合约都有固定的时间期限，而且期货合约只要到期后，该期货合约就会失效，因此本文将记录近半年左右的期货合约的具体数据。文中的Ft是期货价格，St是现货价格，沪银期货价格是其成功上市后沪银1609的每天收盘价格（来源：上海期货交易所，单位：元/千克），沪银的现货价格为中国的沪银合约价格（来源：中国商品交易网，单位：元/千克），本文选取的间隔是从2016-1-5到2016-5-12，而且进行分析的期货价格与现货价格的样本都有46个。最小二乘回归模型的假设中要求误差项的观测值互不相关，而我们的模型中可能存在自相关，所以我们需要对此进行改进，我们采用一阶序列相关来检测序列自相关。

εt=ρεt-1+μt

其中μt为误差修正项。我们改进后建立△Ft和△St的OLS简单回归模型，

△St=α+β△Ft+εt得到的结果如下：

进行OLS回归的结果

（13）式子的结果改为：

即最优套值比率为0.939963，即h*=0.939963。

（二）异方差改进

在利用最小二乘法求取套期保值比率时，预测的误差可能不稳定，也就是说该误差在某一时期可能较小，而在某一时期该误差可能又相对的较大。在求取套期保值比率时，μt的条件方差σt2依赖于很多时刻之前的变化量。也就是说我们在检验中不可能只依赖于一个参数，我们为了计算很多时刻的变化量，就需要对很多个参数进行估计，而这又很难精准的做到。所以我们考虑到扰动项μt的条件方差依赖于它的前期值μt-1的大小，也可以认为t时刻的μt的条件方差σt2依赖于(t-1)的残差平方μt-12，我们用其来度量从前期得到的波动性信息。表达式为：

（14）是σt2的一个分布滞后模型，就可以用一个σt2的滞后值代替许多μt2的滞后值，所以我们进行下一步的改进：

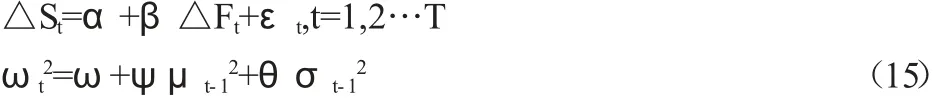
从（15）式，可以得出结论，残差的方差它既与上一期的残差平方有关，也与上一期的预测方差有关。

所以我们进行以下改进:△St=α+β△Ft+εt,其中，εt=ρεt-1+μt，σt2=ω+ψμt-12+θσt-12

这里的最优套期保值比率为0.965265，套期保值效果更好。

三、研究结果总结

本文在对白银的套期比率进行研究的过程中，通过对白银的期现货数据的研究发现，白银的期现货价格间有正相关性，并且它们的相关性很强。采用计量经济学中的一些理论知识，对上海白银期现货价格数据进行分析，得到两者关系如下：第一，上海白银09期货价格与现货价格两者间具备长期的均衡关系；

第二，上海白银09期货与现货市场价格之间具有相互引导的关系，则期货价格能够引起现货价格的改变，白银现货价格能够引起期货价格的改变。白银相关企业能在本文的基础下使用期货市场的价格发现对相关产品定下公道的价格，争取获得最大利益。

[1]徐雪.期货市场——理论与实务[M].北京：中国金融出版社，2010.

[2]何钢.套期保值原理在企业价格规避中的应用[J].经济问题探索，2004，(09)：126-127.

[3]齐明亮.套期保值比率与套期保值的绩效——上海期铜合约的套期保值实证分析[J].华中科技大学学报[社会科学版]，2004，(02)：51-56.

[4]徐金明,张孟喜,丁涛.数值计算方法[M].北京:清华大学出版社，2008:25-60.

[5]魏宗舒.概率论与数理统计数程(第二版)[M].北京:高等教育出版社，2010:33-100.

[6]姜健飞,胡良剑,唐俭.数值分析及其MATLAB实验[M].北京:科学出版社，2004：66-102.

[7]Shao.J.Y.，Zhang L.，Yuan X.Y..On the second Laplacianhao J. Y.，Zhang L.，Yuan X.Y..On The second Laplacian eigenvalues of odd order [J].Linear Algebra and its Applications，2006(419): 475-485.

陈玉秋，女，安徽淮北人，上海海事大学，硕士，研究方向：国际贸易学。

F832

A

1008-4428（2016）11-103-03

指导老师：梁慎刚。