EP-RBF神经网络在时间序列预测中的应用

林丽娜，魏德志，2

(1.集美大学 诚毅学院， 福建 厦门 361021; 2.福州大学 经济与管理学院，福州 350108)



EP-RBF神经网络在时间序列预测中的应用

林丽娜1，魏德志1，2

(1.集美大学 诚毅学院， 福建 厦门 361021; 2.福州大学 经济与管理学院，福州 350108)

为了提高RBF神经网络预测的准确率，提出了一种基于EM聚类算法和改进的PSO算法优化RBF神经网络的混合算法(EP-RBF)。首先，采用EM聚类算法获得初始网络结构，并改进RBF神经网络的径向基函数；然后引入非线性惯性权重和分段变异算子改进PSO算法，增强算法的全局和局部搜索能力，利用改进的PSO优化RBF神经网络的基宽向量、中心矢量、网络权值等参数，提高逼近精度；最后对典型的混沌系统进行验证。结果表明：该混合算法能更好地逼近非线性函数，提高预测准确率。

径向基函数；神经网络；粒子群算法；混沌系统；时间序列

混沌系统具有乱序、无规则、随机、对初始条件依赖等特点，它是研究演化过程的一种科学系统。对混沌系统的研究已经在各行各业得到了广泛的应用。混沌系统时间序列是毫无规律的，要从长期来进行预测非常困难，但在看似无规律的背后，通过对非线性系统的研究可以在短期对它进行预测。用于混沌时间序列预测的方法有神经网络[1-3]、支持向量机[4-5]、误差补偿[5-6]、相空间重构[7-8]、混合模型[9-10]等。支持向量机是一种有关统计学的模型算法，通过对非线性函数的逼近可以获得很好的效果，但是算法的参数选择过于依赖人工。

人工神经网络通过足够时间的训练，对时间序列的预测可以达到很好的精度。RBF网络和其他网络相比，具有拓扑结构简单、学习快速高效的特点，是前向网络的一种主要结构，被广泛应用于实时自适应系统。该网络经过证明只要节点数足够多，可以以任何精度逼近单值函数，因此得到了广泛应用。RBF神经网络应用于预测的难点主要是本身网络结构的确定和相关参数的优化，目前还没有一种方法可以解决这个问题。文献[6]提出一种进化算法改进RBF网络结构和参数，实验结果表明泛化能力得到了提高。文献[7]采用极大熵学习算法改进混沌系统，改善网络的学习和回归能力。文献[8]在确定网络隐含层中心过程中采用了聚类方式，提高网络训练速度。文献[9]提出一种主动控制思想，将系统分解为受控和自由子系统，试验结果表明该方法能抑制抖振，不受外界干扰。文献[10]为了克服RBF网络容易收敛于局部极值的缺点，采用PSO算法进行优化，从而提高逼近的精度。

以上改进方法在一定程度上取得了不错的效果，文献[6-7，10]主要从优化网络参数角度进行改进，文献[8]主要从初始化网络结构、确定隐含层角度进行改进，但是随着混沌理论的发展，并不能满足实际系统要求的高精确度，而且，网络结构和参数优化还有待于进一步提高。因此，本文为了提高预测的精确度，分别从前期初始化网络结构和后期优化网络参数两个角度进行。首先在前期无监督学习中采用EM算法获得网络结构的隐含层的中心点，并改进径向基函数；然后在后期有监督学习中，采用改进PSO进化算法，根据误差不断对网络参数进行优化得到相关网络参数；最后经过混沌时间序列的实验验证，证明EP-RBF方法有较高预测准确性。

1 RBF神经网络

RBF网络是一种三层结构的神经网络：第一层是输入层，第二层是隐含层，第三层是输出层。第一层节点个数通过输入向量x的维数来计算；第二层的节点数根据训练数据点的个数决定，同时和输入层进行连接；第三层的节点数等于输出数据的维数。假设有n个训练样本，则RBF网络结构如图1所示。

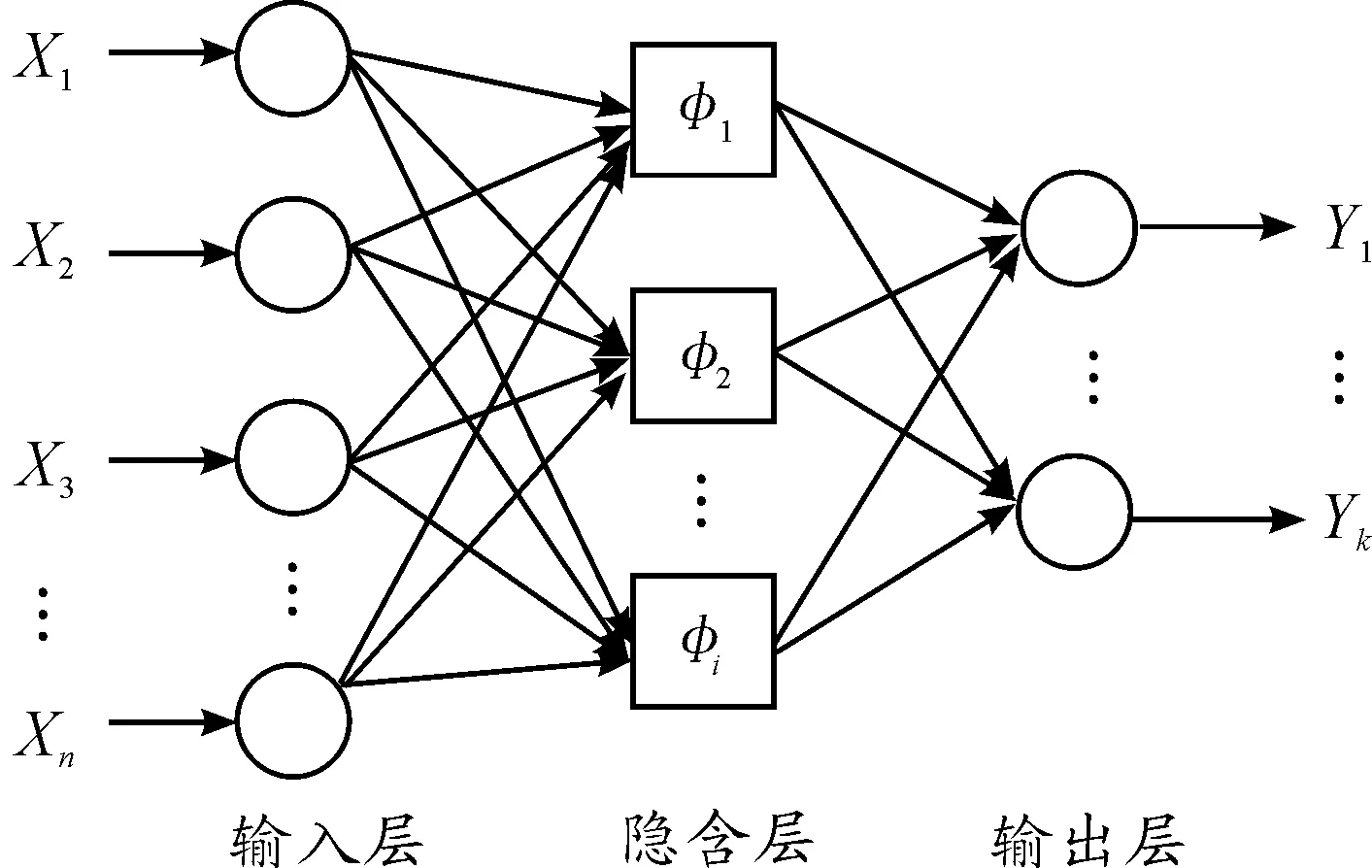
图1 RBF神经网络结构

设输入Xn=[xn1,xn2,…,xnm]，实际输出为Yk=⎣yk1,yk2,…,ykj」，那么从输入到输出的函数映射如式(1)所示。

(1)

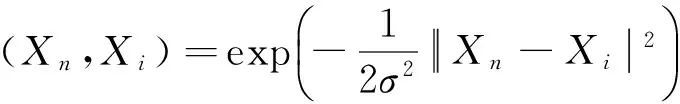
(2)

式(1)中：n为输入样本的个数；J为输出单元的个数；I为隐含层的节点数；Xi=[xi1,xi2,…,xim]为基函数的中心；θj为网络阈值；ωij为网络连接权值。式(2)中：基函数φ采用高斯函数，σ为基宽向量。RBF网络的精度主要由中心节点、基宽向量、阈值、网络值等参数决定，通过对网络参数进行优化，可以提高网络的逼近性能。

2 EM聚类算法结合高斯模型改进径向基函数

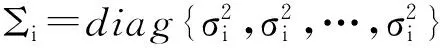
(3)

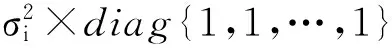
(4)

最大似然估计算法简称EM算法，是一种以统计学为基础、能抗噪音干扰、具有鲁棒性的聚类算法，可以快速有效地计算出式(4)的中心值ui和方差Σi，具体实现过程描述如下。

2) 假设算法已经循环迭代k次，k大于0，根据式(5)计算样本Xn属于各个聚类中心的概率值。

(5)

3) 根据式(6)～(8)计算更新基本参数λ0。

(6)

(7)

(8)

4) 根据式(9)计算最大对数似然估计Ek。如果|Ek-Ek+1|≤ε，其中ε为接近0的自定义值，则算法循环迭代终止，否则程序跳至步骤2)继续循环计算。

(9)

5) 求出最终中心值ui和方差Σi计算的结果，代入式(4)隐含层径向基函数进行求解。

整个算法的核心思想是利用EM算法得到聚类模型的中心值ui和方差Σi，并且把结果直接应用到改进隐含层径向基函数ψ(Xn,ui)中，减少了聚类计算的次数，根据样本的概率值来进行数据对象的分割计算，抗噪音干扰性强，可以进行高维空间计算，算法初始化容易并且收敛快速。

3 改进的PSO算法

PSO算法是一种进化算法，主要根据鸟类捕食行为来进行寻优设计。空间中的每个解通过粒子来表示，最优解根据粒子在空间中的运动不断进行位置和速度的调整来获得。算法的基本思想如下：假设搜索空间为m维，空间有n个粒子，这些粒子组成对应的种群X，则Xn=[xn1,xn2,…,xnm]代表第n个粒子在m维空间的位置；Vn=[Vn1,Vn2,…,Vnm]代表第n个粒子的速度；Pn=[Pn1,Pn2,…,Pnm]代表个体极值；Pg=[Pg1,Pg2,…,Pgm]代表全局极值。算法在每次搜索过程中，粒子通过式(10)和(11)修改自身的位置和速度，不断在空间进行搜索，直到得到最优解。

(10)

(11)

PSO算法具有容易收敛、简单易操作等特点，但是存在着收敛早熟、有一定误差以及不容易进行全局寻最优等缺点。通过引入非线性权重和变异算子，对PSO算法进行修改，解决算法种群多样性不足的缺点。

3.1 非线性权重

惯性权重ω代表的是当前粒子速度和一代粒子的速度的相似性。Shi.Y提出了线性递减惯性权重来提高算法的搜索能力，具体见式(12)。为了解决线性递减惯性权重不能很好处理非线性的问题，本文对式(12)进行改进，提出了一种非线性权重，具体见式(13)。

ω(k)=ωstart-(ωstart-ωend)(kmax-k)/kmax

(12)

(13)

取值ωstart=0.9，ωend=0.4，从图2中根据式(12)和(13)，描述出了权重ω迭代不断变化的整个过程。通过式(13)计算的结果显示变化过程更加平滑稳定，主要原因在于算法开始时，权重取较大的值有利于进行全局计算和查找，在算法后期权重取较小的值对局部计算和搜索有利，从而可以加快整个算法的搜索速度，更快地进行收敛。

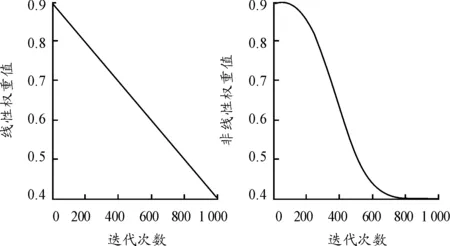
图2 惯性权重ω变化过程

3.2 分段变异算子

目前部分学者把遗传算法中的变异操作引入PSO算法进行改进，主要是根据一定的概率在粒子更新的时候进行变异操作。粒子作为粒子群的一部分在粒子群不断迭代运算过程中，粒子的状态也不断改变，传统的变异操作在这方面的考虑有待提高。本文提出一种分段变异算子，在算法迭代初期对适应度较低的粒子进行变异，把该粒子的位置更新为适应度高粒子的平均值；在后期为了防止算法的早熟现象出现预设一个阈值，让个体和全局极值在一定范围内进行随机变化，具体随机变化的操作见式(14)。

(14)

随机变化的基本思想为：如果大于阈值，按照式(14)进行更新，否则按照式(10)进行更新计算。通过以上利用算子进行分段的变异操作，粒子群在迭代计算中产生更多的多样性，拓展了种群的空间搜索能力，防止出现收敛过早的现象，可更好地得到全局最优解。

4 EP-RBF混合算法

混合算法首先利用了EM聚类算法对RBF结构进行改进，然后利用PSO优化相关结构的参数，最终算法能够有效提高逼近精度，更好地解决非线性系统预测的问题。算法具体流程见图3。

图3 EP-RBF混合算法流程

算法具体步骤如下：

1) 给定神经网络的训练数据集，包含输入和输出样本集；

2) 利用EM聚类算法确定RBF神经网络的中心值ui和方差Σi，并确定径向基函数；

3) 对网络的隐含层中心值、方差、阈值、权值参数进行实数编码，随机产生粒子种群，同时初始化PSO参数；

4) 更新迭代新粒子的速度和位置；

5) 确定PSO算法的适应度函数，采用输出值的均方根误差公式作为适应度的计算公式，具体见式(15)。根据误差适应度函数计算结果对个体和群体极值进行更新。

(15)

6) 判断是否符合算法结束条件，如果不符合，转至步骤4)，如果符合，得到一组最优的网络参数。

7) RBF网络算法进行实验数据训练预测，得到预测结果。

5 实验

5.1 实验条件

本文的实验仿真环境为Matlab2010b，通过神经网络工具箱编写RBF、PSO-RBF、EP-RBF三种神经网络预测算法。对表1中经典非线性混沌系统时间序列进行预测实验，并和参考文献中的其他预测算法进行误差指标对比。

表1 Lorenz非线性混沌系统

(15)

(16)

(17)

(18)

5.2 实验结果

将混沌系统产生的3 000个x分量的时间序列数据分成两种数据样本，分别是训练和预测。其中前2 000个数据作为训练样本，后1 000个数据作为预测样本。表2给出了混合算法和其他算法在误差Rmse、Perr和Smape的比较结果。

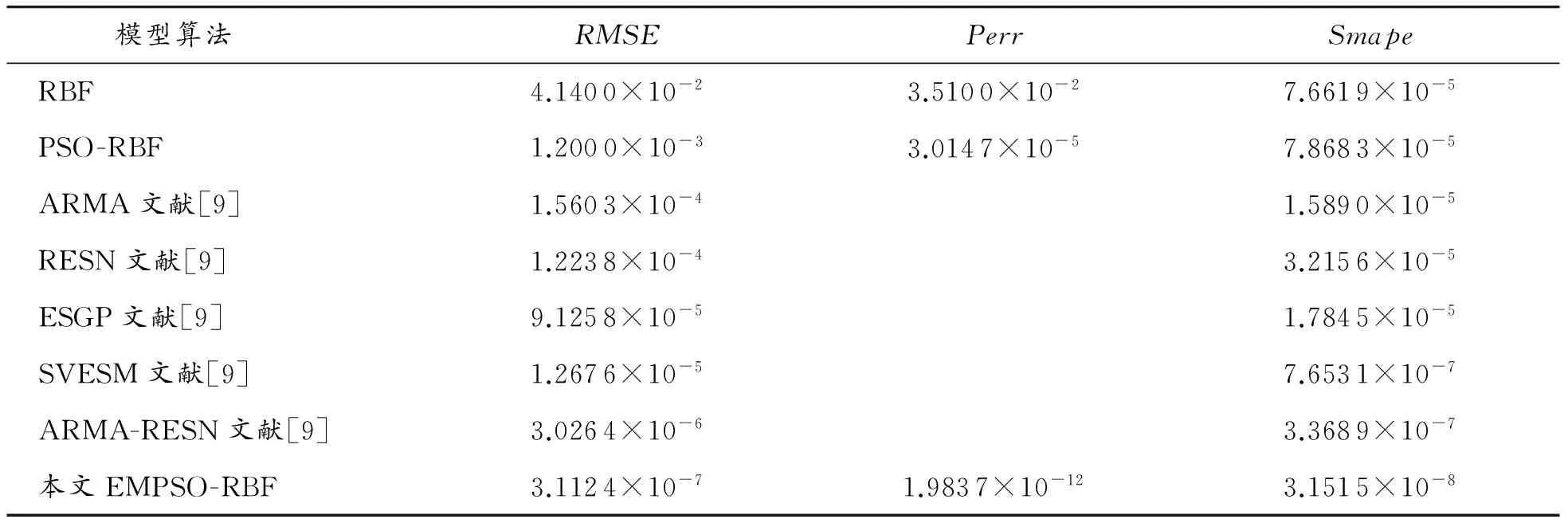
表2 不同模型算法对Lorenz系统预测误差

从表2中可以看出：不同模型算法在误差指标RMSE、Perr、Smape中的表现情况，本文算法相比其他模型算法的误差指标提高了一个数量级左右，得到较好的效果。

6 结束语

本文提出了一种基于EM算法和改进的PSO算法优化RBF神经网络的混合算法EP-RBF。通过利用EM算法和智能算法的优点，提高了对混沌系统的预测精度。对Lorenz混沌系统的实验结果表明，本文模型算法能精确模拟混沌系统的时间序列，适用于混沌系统，适用范围广。同时，在和其他模型算法的比较实验中，本文模型算法在精确度上有较大的提升，达到了一个数量级。

[1] 赵永平,王康康.具有增加删除机制的正则化极端学习机的混沌时间序列预测[J].物理学报,2013,62(24):82-89.

[2] 张学清,梁军.基于EEMD-近似熵和储备池的风电功率混沌时间序列预测模型[J].物理学报,2013,62(5):76-85.

[3] 龙文.基于混合进化算法的RBF神经网络时间序列预测[J].控制与决策,2012,27(8):1265-1268.

[4] 郭会军,刘丁,赵光宙.受扰统一混沌系统基于RBF网络的主动滑模控制[J].物理学报,2011,60(1):104-110.

[5] 肖本贤,王晓伟,刘一福.MPSO-RBF优化策略在锅炉过热系统辨识中的仿真研究[J].系统仿真学报,2007,19(6):1382-1385.

[6] 赵永平.过滤窗最小二乘支持向量机的混沌时间序列预测[J].物理学报,2013,62(12):113-121.

[7] 黄敏,胡学钢.基于支持向量机的网络舆情混沌预测[J].计算机工程与应用,2013,49(24):130-134.

[8] 张金良,谭忠富.混沌时间序列的混合预测方法[J].系统工程理论与实践,2013,33(3):763-769.

[9] 唐舟进.基于迭代误差补偿的混沌时间序列最小二乘支持向量机预测算法[J].物理学报,2014,63(5):78-87.

[10]AMJADY N,KEYNIA F.Day-ahead price forecasting of electricity markets by a mixed model and hybrid forecast method[J].International Journal of Electrical Power & Energy Systems,2008,30(9):533-546.

(责任编辑 杨黎丽)

The Application of EP-RBF Neural Networks in the Prediction of Time Series

LIN Li-na1, WEI De-zhi1，2

(1.Chengyi College, Jimei University, Xiamen 361021,China;2.School of Economics and Management, Fuzhou University, Fuzhou 350108, China)

A hybrid algorithm (EP-RBF), which was optimized by the EM clustering and improved PSO,was proposed in order to improve the prediction accuracy of RBF neural network. Firstly, the network structure was initialized by EM clustering algorithm, and the radial basis function of RBF neural network was improved. Then the nonlinear inertia weight and sectional mutation operator were introduced to improve the PSO in order to improve theglobal and local search ability, and the base width vector, center vector, network weights and other parameters of the RBF neural net work was optimized by the improved PSO in order to improve the accuracy of approximation. Finally, the several typical chaotic systems were verified to show that the hybrid algorithm can approach the nonlinear function better and improve the accuracy of prediction.

radial basis function;neural network;particle swarm optimization algorithm;chaotic system;time series

2016-03-18 基金项目：国家自然科学基金资助项目 (71271056)；福建省教育厅资助项目(C13001，JA14368)

林丽娜(1984—)，女，硕士,讲师，主要从事网络安全与网络舆情研究，E-mail:linda_839@126.com；魏德志(1982—)，男，副教授，博士研究生，主要从事网络安全与网络舆情研究。

林丽娜，魏德志.EP-RBF神经网络在时间序列预测中的应用[J].重庆理工大学学报(自然科学)，2016(11):121-126.

format：LIN Li-na,WEI De-zhi.The Application of EP-RBF Neural Networks in the Prediction of Time Series [J].Journal of Chongqing University of Technology(Natural Science)，2016(11):121-126.

10.3969/j.issn.1674-8425(z).2016.11.020

TP393

A

1674-8425(2016)11-0121-06